どうも、木村(@kimu3_slime)です。
今回は、勉強ができるようになる方法として、記憶、思考、興味という3つの要素に注目して考えていきます。
自分も基本的にこの認識。
最重要の少数の原理・定義は暗記(記憶)する。しかしそれだけでは応用が効かない(問題のパターンが多すぎる)から、原理や定義の使い方を学んでいく。
暗記は強力だが、スケールしない。記憶のキャパはそんなにない。だから途中で思考やロジックの力でスケールさせる。— 木村すらいむ (@kimu3_slime) July 22, 2022
記憶力をフルに活用するには、努力やかけた時間というよりは、記憶する対象に関する興味関心が大事。面白くないことは覚えられないし、面白ければ細かいこともたくさん覚える。オタク・マニアがそう。
知識の勝負は、好きでやってるやつには基本勝てない。「趣味の大学数学」の名付けもその要素。— 木村すらいむ (@kimu3_slime) July 22, 2022
暗記VS思考:暗記への依存を減らす
勉強において
- 暗記力(記憶)が大事
- 思考力が大事
という2つの要素はしばしば対立して語られますが、両方育てていけば良いものです。
あえて言えば、中学や高校、大学と、学ぶ内容が増えるにつれて、思考力を伸ばしていくのが大事です。
暗記や公式、パターンマッチをするだけが勉強という考え方だと、学ぶ内容が増えるにつれ、覚えきれずについていけなくなるでしょう。
例えば、暗記や記憶は、ものすごく強力なツールです。難しい問題でも、解説してもらった直後ならば、短期記憶を使って回答を再現することはできるでしょう。
しかし、どんな人であっても、暗記できる量には限界があります。もし教科書に書いてあることをすべて暗記できるならば悩みは減りますが、多くの人はそうではありません。だから、頭を使って、記憶に頼りすぎずに多くの問題を解けるようになるわけです。
- 最重要の定義や原理は暗記・記憶する
- 記憶だけでは問題のパターンの多さに対処できない、教えられたことしかできないので、定義や原理の使い方を学ぶ(思考力を鍛える)
というやり方が有効だと経験的に考えています。
例えば小学校では、ひらがなといった文字や単語の意味、数字や掛け算九九を学びますが、かなり暗記に寄った学習です。大変ですが、それだけ人生の至る所で使うようなアイデアだから、覚える価値があるわけですね。
一方で中学校や高校では、小学校で学んだことはベースとして、それらを組み合わせて発展していきます。だんだんと、「覚える」だけでは対処できなくなっていくでしょう。僕は中学1年の国語や歴史の段階で無理でした(笑)。
「勉強はたくさん覚えなければならないことがあって大変だ」と思うならば、覚えなくて良い方法を考えましょう。関連付け、論理、パターン化によって、知るべき内容を圧縮しましょう。
数学では方程式\(x+3=5\)を\(x=5-3\)と変形することを、「移項」と呼んだりします。これを特殊なルールだと思って学ぶと、\(3x=5\)を\(x=\frac{3}{5}\)という変形が理解しにくかもしれません。
「等号=は左側と右側が同じ値であることを意味する」という定義、「同じものに、同じものを引いたり、同じもので割ったりしても等しいまま」という考え方(等式の性質)を知れば、当たり前のこととして覚えるまでもなくなるでしょう。
記憶を成長させる方法
「暗記には限界があるから頭を使え」が僕の基本的な勉強法ですが、それでも「記憶を使うな」とは言いません。
結局どれだけ頭を使ったところで、最低限の原理や定義は覚えておく必要があります。
覚えることも、工夫によって上達します。僕は大学受験のときに勉強法を調べていて、玉石混交の情報の中から、エビングハウスの忘却曲線の理論を知りました。
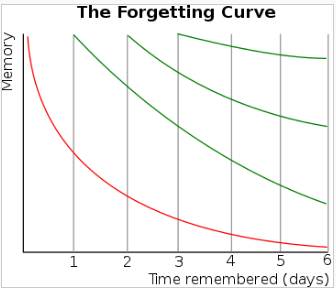
実験の対象者に無意味な音を覚えさせ、何日後までにどれだけの割合覚えているかを曲線で表したものです。赤い曲線を見ると、1日で半分は忘れ、一週間経てばほぼすべて忘れてしまうわけです。確かに体感でこういう経験はあって、だから記憶はアテにならないと思います(笑)。
しかし、長期的に覚えられていることもあります。それは間を空けて反復(リハーサル)をしているからです。1日後に反復すると、記憶は100%に戻りますが、時間経過したときの減少率まで変わっていることが読み取れますね。4回目の反復では、記憶の減少率がかなり小さくなり、中期や長期の記憶に移行しつつありそうです。
僕はこの方法を受験勉強で試してみて、英単語を効率よく覚えられることがわかりました。最初のうちはすぐ忘れてしまうので、反復のペースを半日程度にしておきます。定着してきた単語は1日おき程度のチェックにし、1周間残るならもうその単語は覚えきったものとしました。
どんなに勉強に時間をかけようが、反復していない物事は忘れていくのが普通です。結局忘れてしまうなら勉強なんて無意味かというとそうではなくて、それは忘却曲線が示すように、記憶として定着しやすくなっていくわけですね。
特にこれといって「勉強」をしなくても、文字の読み方や簡単な計算はできる人が多いでしょう。それは反復をして思い出すまでもない当たり前の記憶となっているからです。そういう当たり前の領域を伸ばしていく勉強は、成長を感じられて面白いですね。
興味が全体を底上げする
忘却曲線の理論を試していて気づいたのは、結局は
- 記憶には時間がかかる
ということです。何日もまたぐ反復をして、それでようやく短期記憶は長期記憶へと移行していくわけです。学問は一朝一夕では身につかず、一夜漬けや短期の試験対策は、一ヶ月もしたら消えてしまうでしょう。
同時に気づいたこととして、
- 記憶には気力がかかる
ということです。例えば無意味な単語の羅列を覚えよと言われても、心理学の実験で何かしらの報酬が得られるといった状況でなければ、やる気がでないでしょう(笑)。
記憶を定着させるためには反復が必要ですが、反復をするためにはやる気が必要なのです。
子どもでもすぐれた知識を持つ人はいて、例えば歴史オタクや鉄道オタクなど、さまざまな分野でオタクやマニアはいます。僕は専門家や研究者は、究極のオタクだと考えています。
彼らの知識が多いのは、「勉強しろ」と言われて身についたものではないでしょう。興味があるから、あれもこれもと調べて勝手に詳しくなっていったのです。
自分の知識や記憶がどうやって定着したか思い出してみましょう。面白くないと思った勉強はなかなか覚えられないし、面白いと思ったことは細かいこともたくさん覚えられます。
知識の勝負は、好きでやってるやつには基本勝てません。このサイトは「趣味の大学数学」ですが、「趣味」はただ単に楽しむだけでなく、「楽しむことが結果的に成長につながる」というニュアンスもあります。
もちろん、学びは勝負の世界ではありません。他人と比較して自己評価が下がるほど不毛なことはないので、自分なりの楽しみ方を見つけるのが良いですね。
その上で、趣味で楽しむことが目的であったとしても、ある程度は切磋琢磨したり、ガチで真面目にやったほうが楽しめると思っています。「成長しない自分に飽きる」理論で、向上しようとしないと、刺激が足りずに飽きてしまって、結果的に長いこと楽しめなくなってしまうんですよね。
以上、勉強ができるようになる方法として、記憶、思考、興味という3つの要素を紹介してきました。
- 暗記には限界があるから頭を使おう
- 記憶のコツは反復すること
- 思考も記憶も、結局楽しみが必要
無理強いして「頑張って」やるようなことは、結局成長するのが難しいと思います。
自分が楽しいと感じること、楽しそうだなと思うことに取り組めば、自然と頭を使い記憶できることも増え、勉強ができるようになるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
ディスカヴァー・トゥエンティワン (2019-03-14T00:00:01Z)
¥3,080 (コレクター商品)
森北出版 (2022-03-08T00:00:01Z)
¥2,900 (中古品)
こちらもおすすめ