ひし形、たこ形四角形の面積の求め方、証明

どうも、木村（@kimu3_slime）です。

今回は、ひし形、たこ形四角形の面積の求め方、証明を紹介します。

ひし形、たこ形四角形の面積の求め方
対角線が直交する四角形の面積
こちらもおすすめ

ひし形、たこ形四角形の面積の求め方

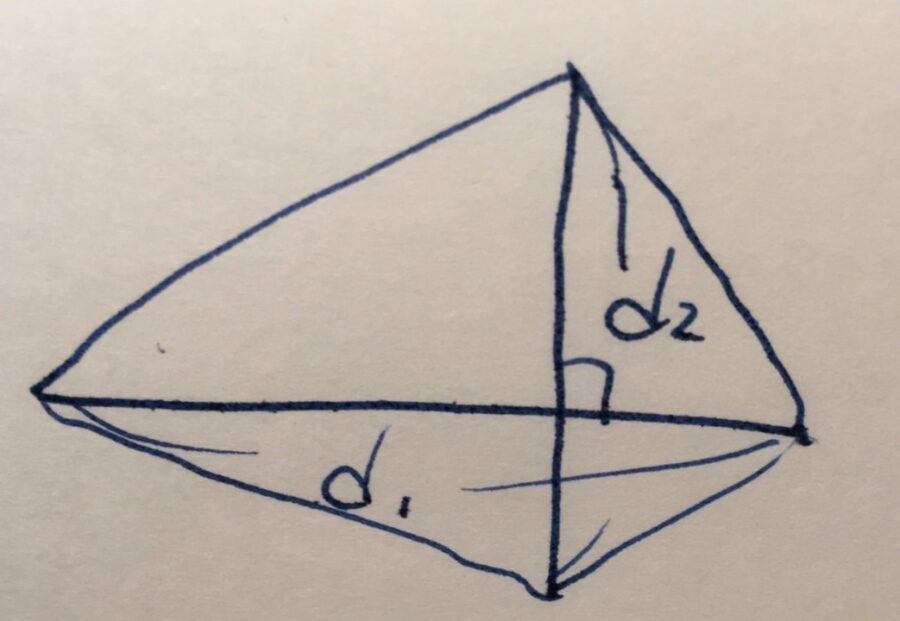
ひし形（隣り合う辺の長さが等しいペアが2組ある平行四辺形）の面積は、その対角線の長さを\(d_1,d_2\)として、

\[S= \frac{1}{2}d_1d_2\]

によって求められます。「対角線1かける対角線2、割る2」です。

隣り合う辺の長さが等しいペアが2組ある四角形、（広義の）たこ形四角形の面積も、

\[S= \frac{1}{2}d_1d_2\]

となります。

特殊なケースとして、正方形はひし形の一種です。辺の長さを\(a\)とすると、対角線の長さはピタゴラスの定理から\(d_1,d_2 = \sqrt{2} a\)です。ひし形の面積の等式にあてはめれば、

\[S= \frac{1}{2}(\sqrt{2}a)^2 \\ = \frac{1}{2}2 a^2= a^2\]

となり、確かに正方形の面積の計算式が現れます。長方形でも同様の議論ができます。

つまり、「ひし形の面積は対角線の積割る2」は、正方形や長方形の面積の式の一般化となっているわけです。

対角線が直交する四角形の面積

なぜこの方法で面積が求められるのでしょうか。

ひし形、たこ形四角形には共通して、2つの対角線が直交するという性質があります。

そして、直交する対角線を持つ四角形の面積は

\[S= \frac{1}{2}d_1d_2\]

となるのです。今回は、面積がこれによって求められることを証明しましょう。

長さ\(d_1,d_2\)の直交する対角線を持つ四角形を\(ABCD\)とし、対角線の交わる点を\(E\)としましょう。

この図形の面積の問題を、長方形の面積の問題に帰着させましょう。

対角線に平行な直線を角頂点に対して引き、それらの交点を\(H,I,J,K\)とします。

これらによって、4組の合同な三角形ができたことを示しましょう。

\(\triangle ABE,\triangle BAF\)に注目します。それらを合わせた四角形\(FBEA\)は、平行な直線を引いたことから、向かい合う2組の辺が平行であり、平行四辺形です。\(AB\)がその対角線となります。一般に、平行四辺形の対角線によってできる2つの三角形は合同なので、\(\triangle ABE,\triangle BAF\)は合同です。

他の3組の三角形も、全く同様にして、合同となります。

一般に、合同な図形の面積は等しく、部分に分けて計算できます（面積の定義・公準）。したがって、

\[\begin{aligned} &(FGHIの面積) \\ &=(ABEの面積)+(BAFの面積)\\&+ (BCEの面積)+(CBGの面積)\\&+ (CDEの面積)+(DCHの面積)\\&+ (DAEの面積)+(ADIの面積) \\&=2\times((ABEの面積)+ (BCEの面積) \\& +(CDEの面積)+(DAEの面積)) \\&=2\times(ABCDの面積)\end{aligned}\]

となります。三角形の合同から、対角線の長さ\(d_1,d_2\)は、長方形\(FGHI\)の辺の長さに等しいです。よって、長方形の面積は2つの隣り合う辺の積なので、

\[\begin{aligned} & (ABCDの面積)\\ &=\frac{1}{2}\times (FGHIの面積)\\ &= \frac{1}{2}d_1d_2 \end{aligned}\]

となることが示せました。

以上、ひし形、たこ形四角形の面積の求め方、証明を紹介してきました。

これらは共通して対角線が直交するという性質があり、直交しているとその面積が拡大した長方形の半分となる、というわけですね。

計算式だけでなく、幾何学的な背景も理解すると覚えやすいでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。