どうも、木村(@kimu3_slime)です。
今回は、たこ形四角形の定義、大きさの等しい向かい合う角があることの証明を紹介します。
たこ型四角形の定義
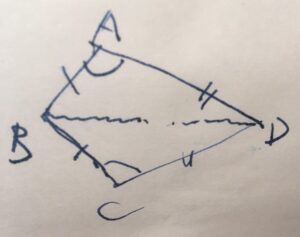
たこ形四角形(凧形、カイト kite)は、隣り合う辺の長さが等しいペアが2組あるような四角形のことです。海を泳ぐタコ(蛸)ではなく、空に飛ばすタコ(凧)の形です。
平行四辺形とは、向かい合う辺の長さが等しいペアが2組あるような四角形のことでした。たこ形は、「向かい合う」が「隣り合う」に変わった定義をしていますね。
細かく分けると、狭義のたこ形、広義のたこ形の定義があります。
狭義のたこ形は、隣り合う辺の長さが等しいペアが2組あり、それらのペアで異なる長さを持つものとされます。この定義では、見た目がたこ形らしいものだけを指し、ひし形や正方形は狭義のたこ形ではありません。
広義のたこ形は、隣り合う辺の長さが等しいペアが2組あり、それらのペアが同じ長さであっても良いとされます。ひし形や正方形は、広義のたこ形です。
大きさの等しい向かい合う角があることの証明
たこ形四角形の性質として、大きさが等しい向かい合う角が必ずひとつは存在することがあります。
狭義のたこ形では、長さの異なる辺に挟まれる角同士の大きさが必ず等しくなります。

\(AB=BC\)、\(CD=DA\)となっているたこ形の四角形を考えましょう(\(AB \neq CD\)であって良い)。このとき、\(\angle BAD =\angle BCD\)となることを証明します。
対角線\(BD\)を考えましょう(定規による作図)。すると、2つの三角形\(\triangle ABC, \triangle BCD\)ができます。
仮定より、\(AB=BC\)、\(CD=DA\)です。さらに、共通する辺として\(BD= BD\)です。
よって、三角形の合同条件、3つの辺の長さが等しい(SSS)から、三角形\(\triangle ABC, \triangle BCD\)は合同です。
特に、対応する角の大きさは等しいので、\(\angle BAD =\angle BCD\)となることが示せました。
ちなみに、長さの等しい辺によって挟まれる角同士の大きさは、等しいとは限りません。
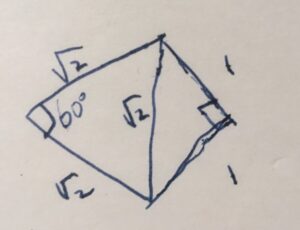
上の図の左形は正三角形、右側は直角三角形です。これらをくっつけてできた四角形は、たこ形の定義を満たしていますね。
長さの等しい辺に挟まれる角度は、それぞれ\(60^{\circ},90^{\circ}\)であり、等しくありません。
広義のたこ形では、2組の向かい合う角が等しくなりえます。例えば、ひし形や正方形がそうですね。
以上、たこ形四角形の定義、大きさの等しい向かい合う角があることの証明を紹介してきました。
小中学校の算数・数学において、平行四辺形やひし形に比べてたこ形はマイナーですが、四角形の一種として知っておくと良い形ですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)