どうも、木村(@kimu3_slime)です。
今回は、ピタゴラスの定理の相似による証明を紹介します。
直角三角形\(ABC\)について考えましょう。
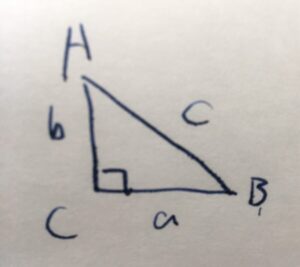
斜辺の長さを\(c\)、他の2つの辺の長さを\(a,b\)とすると、\(a^2 +b^2 =c^2\)という等式が成り立ちます。
これがピタゴラスの定理(三平方の定理 Pythagorean theorem)です。
では、証明していきましょう。ピタゴラスの定理は、面積を使った方法など、さまざまな証明が知られています。
今回は、補助線を引き、相似な三角形を見出す方法です。
斜辺\(AB\)から点\(C\)に垂線を引き、交わる点を\(D\)とします。
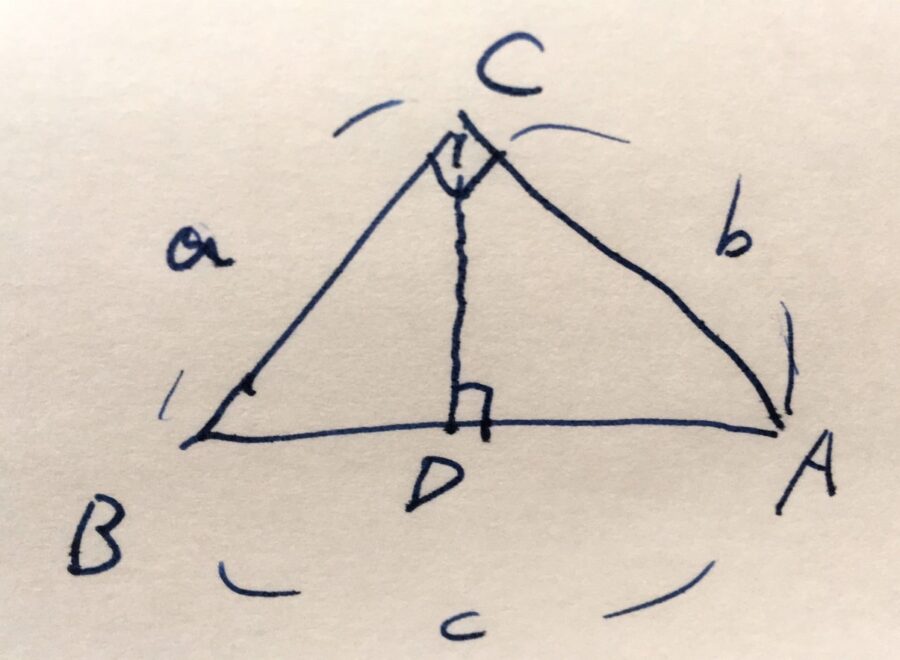
分割されできた三角形\(\triangle CBD\)が、もとの三角形\(\triangle ABC\)と相似であることを示しましょう。
\(CD\)は\(AB\)の垂線なので、\(\angle CDB = \angle ACB=90^{\circ} \)です。また、共通する角として、\(\angle CBD =\angle ABC\)です。
したがって、三角形の相似条件、2つの角度が等しいので(AA)、\(\triangle CBD,\triangle ABC\)は相似です。
特に\(BD\)の長さについて、辺の長さの比が一定なので、\(\frac{BD}{CB}=\frac{BC}{AB}\)で、\(BD = \frac{a}{c} \times a = \frac{a^2}{c}\)と表せます。
\(\triangle ACD,\triangle ABC\)についても同様の考察ができます。
\(CD\)は\(AB\)の垂線なので、\(\angle CDA = \angle ACB=90^{\circ} \)です。また、共通する角として、\(\angle CAD =\angle BAC\)です。
よって、三角形の相似条件、2つの角度が等しいので(AA)、\(\triangle ACD,\triangle ABC\)は相似です。
辺の長さの比は一定なので、\(\frac{AD}{AC}=\frac{AC}{AB}\)で、\(AD= \frac{b^2}{c}\)となります。
長さの情報を\(c=BD+AD\)とまとめれば、\(c= \frac{a^2}{c}+\frac{b^2}{c}\)です。これに\(c\)をかければ、\(a^2 +b^2 =c^2\)が示せました。
以上、ピタゴラスの定理の相似による証明を紹介してきました。
斜辺を利用して三角形を作ると、それが元の三角形に相似になるので、斜辺の長さとそれ以外の辺の長さに等式ができあがる。両者に共通する辺の情報を用いているから、辺の長さの2乗の形が出てくるというわけですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)