どうも、木村(@kimu3_slime)です。
今回は、関数項級数の一様収束、ワイエルシュトラスのMテストとは何か、熱方程式への応用を紹介します。
ワイエルシュトラスのMテストとは
べき級数\(\sum_n a_n (x-a)^n\)やフーリエ級数\(\sum_n a_n \sin n\pi x\)のように、関数の和として表される級数\(\sum _n f_n(x)\)を関数項級数(function series)と呼びます。
その級数が収束し、さらに微分できるかどうかは重要な問題です。多項式・有限和なら当然微分できるわけですが、級数・無限和となると例外も起こりえます。
一般に、関数項級数は、それが一様収束するならば、項別微分・項別積分可能であることが知られています。
そしてその一様収束の十分条件を与えてくれるのが、ワイエルシュトラスのMテストです。
ワイエルシュトラスのMテスト(Weierstrass M-test)
\(A\subset \mathbb{R}^N\)、\(f_n: A\to \mathbb{R}\)とする。
- すべての\(n\)に対し\(\sup _{x \in A} |f_n(x)| \leq M_n\)
- \(\sum_{n}^\infty M_n\)は収束する
を満たす数列\((M_n)\)が存在するならば、関数項級数\(\sum_{n}^\infty f_n\)は\(A\)上で一様収束する。
収束することとコーシー列であることを言い換えて示せます。証明について詳しくは、杉浦「解析入門 Ⅰ」を参照。
熱方程式への応用
僕は関数項級数やMテストの話を学んだとき、いまいちそれを何に応用するのかわかりませんでした。そこで今回は、熱方程式への応用を紹介します。
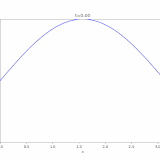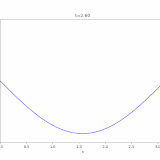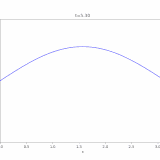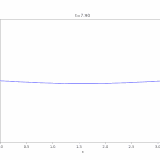
1次元熱方程式、ディリクレ境界条件での解は、
\[ \begin{aligned}u(x,t)=\sum_{n=1}^\infty u_n(x,t)\\= \sum _{n=1} ^\infty c_n e^{-n^2 \pi^2 t} \sin n\pi x\end{aligned} \]
と表すことができます。この級数が一様収束し、項別微分可能であることを示しましょう。ただし、係数は
\[ \begin{aligned}c_n = 2 \int _0 ^1 g(x) \sin n\pi x dx\end{aligned} \]
です。
級数の一様収束
Mテストを利用するためには、\(x\)に依存せず一様に\(|f_n(x)|\)を評価し、収束する級数で抑えることです。
まず、係数\(c_n\)は、(\(g\)が可積分ならば)有界です。積分の三角不等式、三角関数の大きさの最大値は1であることより、
\[ \begin{aligned} |c_n| & \leq 2 \int _0^1 |g(x) \sin n\pi x |dx \\& \leq 2\int _0^1 |g(x)| dx \\&=:& M \end{aligned} \]
となるので。
\(t_0 >0\)を任意とし、\(A:=[0,1]\times (t_0, \infty)\)としましょう。そこで関数\(u_n\)を評価すると、
\[ \begin{aligned} |u_n(x,t) | &= |c_n e^{-n^2 \pi^2 t} \sin n\pi x| \\ & \leq Me^{-n^2 \pi^2 t_0} \\ &=:& M_n\end{aligned} \]
となります。この\(M_n\)は、\(x,t\)に依存していないのが重要です。
多項式と指数関数の発散のスピード比較から、\(\lim_{n\to \infty}n^2 M_n=0\)です。したがって、十分大きな\(n\)に対し、
\[ \begin{aligned}M_n \leq \frac{1}{n^2}\end{aligned} \]
とできます。\(\sum_{n}\frac{1}{n^2}\)は収束するので、Mテストから一様収束が言えました。
参考:負のべき乗の無限級数Σ1/n^pの収束・発散の判定方法
時間微分
時間微分についても、ほぼ同様です。
まず、各項\(u_n\)は\(t\)について微分可能で、
\[ \begin{aligned}\frac{\partial u_n}{\partial t} = -c_n n^2 \pi^2 e^{-n^2 \pi^2 t} \sin n\pi x\end{aligned} \]
となります。これらのなす級数が一様収束することを示しましょう。
\(A\)上において、各項の大きさは
\[ \begin{aligned} |\frac{\partial u_n}{\partial t}| & \leq M\pi^2 n^2 e^{-n^2 \pi^2 t_0} \\ &=:&M_n\end{aligned} \]
と評価できます。
多項式と指数関数の発散のスピード比較から、\(\lim_{n\to \infty}n^4 M_n=0\)です。したがって、十分大きな\(n\)に対し、
\[ \begin{aligned}M_n \leq \frac{1}{n^2}\end{aligned} \]
とできます。\(\sum_{n}\frac{1}{n^2}\)は収束するので、Mテストから一様収束が言えました。
したがって、項別微分定理より、\(u\)は\(t\)について微分可能で、\(\frac{\partial u}{\partial t}=\sum _n \frac{\partial u_n}{\partial t}\)となります。
空間微分
さらに、2回空間微分可能であることを示しましょう。
\[ \begin{aligned} |\frac{\partial u_n}{\partial x}| &= |c_n n\pi e^{-n^2\pi t} \cos n\pi x| \\& \leq Mn\pi e^{-n^2 \pi^2 t_0} \end{aligned} \]
\[ \begin{aligned} |\frac{\partial^2 u_n}{\partial x^2}| &= |-c_n n^2\pi^2 e^{-n^2\pi t} \sin n\pi x| \\& \leq Mn^2\pi^2 e^{-n^2 \pi^2 t_0} \end{aligned} \]
なので、同様にしてMテストからこれらの級数は一様収束します。
項別微分定理から、\(u\)は\(x\)について2回微分可能で、\(\frac{\partial^2 u}{\partial x^2} =\sum_n \frac{\partial^2 u_n}{\partial x^2}\)と言えました。
今回は熱方程式を題材としましたが、波動方程式についても同様の方法で微分可能性を示せます(試してみてください)。
以上、関数項級数の一様収束、Mテストとは何か、熱方程式への応用を例に紹介してきました。
一様収束は項別微分・積分のために重要な概念ですが、その典型的な応用としては熱方程式やフーリエ級数があります。もし一様収束の学びに疑問を抱いたら、関数項級数が具体的に登場する話:熱方程式やフーリエ級数について学んでみると良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
東京大学出版会 (1980-03-31T00:00:01Z)
¥2,150 (中古品)
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
熱方程式の解き方:変数分離法、フーリエ級数展開(1次元、有界領域)