どうも、木村(@kimu3_slime)です。
前回、生き物の個体数の変化のモデル、最初はグッと増えて後に伸びが悪くなる、ロジスティック方程式を紹介しました。
それは1種の生物の個体数の変動を表すものでした。現実には、多種の生物が生きていて、食ったり食われたりする関係にある生物もいます。例えば、キツネはウサギを食べます。
今回は、2種の生物の個体数の変動、食う食われるの関係のモデルとして、捕食者-被食者モデル(ロトカ・ヴォルテラ方程式)を紹介します。
捕食者-被食者モデル(ロトカ・ヴォルテラ方程式)とは
おさらいをしましょう。ロジスティック方程式は、次のような方程式でした。
\[ \begin{aligned}\frac{du}{dt}= ru – \frac{r}{K} u^2\end{aligned} \]
\(u(t)\)が個体数を表す関数で、\(r,K>0\)は定数でした。
2種の生物\(u(t),v(t)\)に関する方程式を考えてみましょう。食われる方を被食者(prey)\(u\)、食う方を捕食者(predator)\(v\)と呼びます。
次の方程式が、捕食者-被食者モデル(predator-prey model)、またはロトカ・ヴォルテラ方程式(Lotka-Volterra equations)です。
\[\frac{du}{dt}= au – buv \\ \frac{dv}{dt}= cuv – dv\]
ここで\(a,b,c,d>0\)は定数です。捕食者が\(v\)、被食者が\(u\)です、順序に注意してください。
式の意味を読み解きましょう。
\(au\)は被食者\(u\)の指数的増加、\(-dv\)は捕食者\(v\)の指数的減少を意味します。これはマルサスモデルと同じです。被食者は増えやすく、捕食者は餌がなければ減っていくという法則。
ポイントは、相互に関係を及ぼす項\(uv\)です。\(uv\)が増えるほど、被食者は減り、捕食者は増えます。
ヴォルテラは、魚の個体数が周期的に変化することを数学的に調べようとして、方程式を導いたそうです。
この方程式の解は、どのようなものでしょうか? 力学系の手法で調べてみましょう。
参考:方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門
ロトカ・ヴォルテラ方程式の平衡点を調べてみましょう。
平衡点は\((u,v)=(0,0),(\frac{d}{c},\frac{a}{b})\)の2つです。
それぞれの平衡点における線形化行列は
\[ \begin{aligned} \begin{pmatrix} a & 0 \\ 0 & -d \end{pmatrix} \end{aligned} \]
\[ \begin{aligned} \begin{pmatrix} 0 & -\frac{bd}{c} \\ \frac{ac}{b} & 0 \end{pmatrix} \end{aligned} \]
であり、それぞれの固有値は\(a,-d\)と\(\pm\sqrt{-ad}\)です。
したがって、\((u,v)=(0,0)\)は不安定、\((\frac{d}{c},\frac{a}{b})\)はリヤプノフの意味で局所的に安定です。
さらに、\(V(x,y)= -d \log u + cu – a \log v + b v\)とすると、これはリヤプノフ関数となっており、より広い範囲でリヤプノフ安定と言えます。
参考:線形微分方程式の解の安定性は「固有値」を調べればわかる、微分方程式の安定性を調べる「線形化」の方法とは?、安定性を判別するリヤプノフ関数の方法とは?
つまり、解の挙動はおよそ次のような図になります。(正確な円ではなく、卵のような形に歪んだ閉軌道になる)
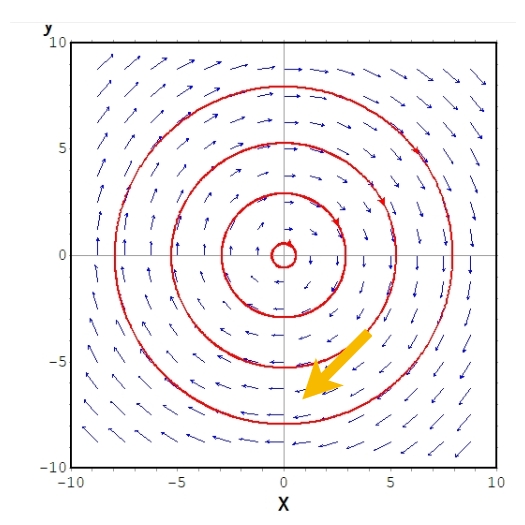
解は周期的で、
- 先に捕食者が減り、次いで被食者が減る
- 先に被食者が減り、次いで捕食者が増える
- 先に捕食者が増え、次いで被食者が増える
- 先に被食者が増え、次いで捕食者が減る
という繰り返しになります。被食者が食われれば減り、エサが減った捕食者は減り、天敵が減れば被食者が増え、被食者が増えればまた捕食者が増える……という食う食われるの循環が感じられますね。
数値シミュレーションを行うと、次のような画像になります。
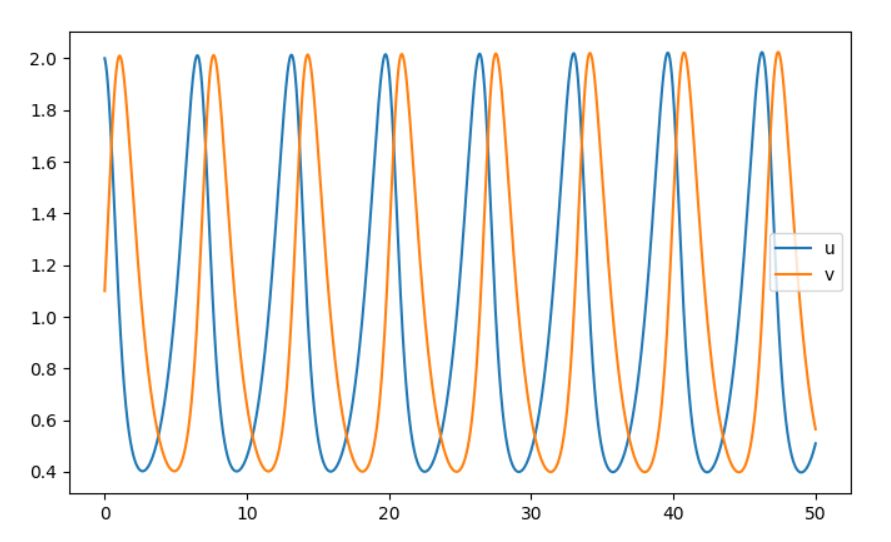
参考:ルンゲ=クッタ法:常微分方程式をPythonで解く原理を解説
被食者-捕食者モデルは、現実に起こる個体数変動を説明するものなのでしょうか?
次の図のように、ヤマネコとウサギの個体数の周期的な増減が見られる例があります。

画像引用:巌佐
しかしながら、これがヤマネコ(捕食者)とウサギ(被食者)の食う食われるの関係によって起こっている現象かどうかは定かではありません。もしかしたら、ウサギとそのエサである植物との関係で振動が起こっているのかもしれません。
巌佐によると、野生の生物で個体数の周期的な振動はあるが、それが被食者捕食者の相互作用によって生じていることがはっきりと確かめられた例はないそうです。
一方、植食性のダニと捕食性のダニに関する実験例では、周期的な変動が起こっているそうです。
上で紹介したロトカ・ヴォルテラ方程式は、シンプルですが、不十分な点もあります。
例えば、方程式がほんの少し変わっただけで解の挙動が変わってしまいます(構造安定ではありません)。実部ゼロの固有値が問題です。
この場合は、モデルを少し変えることで、安定な周期解(リミットサイクル)が存在するような(構造安定な)方程式にすることができます。
参考:力学系の構造安定性について簡単に紹介、極限集合の性質を明らかにするポアンカレ・ベンディクソンの定理
ロジスティック方程式のときと同様、上で示したタイプの項だけでなく、それをもとに変えた方程式の性質を調べていくことができます。もちろん、2種間の関係だけでなく、3種、n種の方程式を考えることもできるでしょう(式はより複雑になりますが…)。
被食者-捕食者の関係ではなく、2種の生物が共有の食べ物や居場所を求め合うモデル、競争モデル(competition model)と呼ばれるものも存在します。
\[\frac{du}{dt}= r_1 u(1 -\frac{u+a v}{K_1}) \\ \frac{dv}{dt}= r_2 v(1 -\frac{bu+ v}{K_2})\]
2種の競争系では周期解は存在しませんが、3種の場合は存在することが知られています。
参考:種間相互作用と生物群集の数理モデル – 数理解析研究所講究録
ロトカ・ヴォルテラ方程式は、2種の生物の個体数の変化のようすを分析するときに使える方程式です。
その解の挙動がどうなっているのかは数学的な問題、モデルと現実がマッチしているかを問うのは生物学的な(生態学的な)問いです。
こうした問題を扱う分野は数理生物学(mathematical biology)と呼ばれます。まさに数学が応用として活かされている例と言えるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版
売り上げランキング: 213,065