どうも、木村(@kimu3_slime)です。
微分方程式の解の挙動は、一般に複雑なものです。例えば、3次元の(連続)力学系でもカオスを示す例があります(ローレンツ方程式)。
しかしながら、2次元の連続力学系では、カオスが起こらず、解の挙動は比較的単純となることが知られています。
これを保証するのが、ポアンカレ・ベンディクソンの定理と呼ばれる定理です。
今回は、その定理と、それを理解するために必要な極限集合の概念を紹介します。
解のω-極限集合、リミットサイクルの定義
解の極限集合とは、ある点を出発した解が、限りなく時間が経ったときに近づいていく点の集合のことです。
方程式\(\dot{x} = f(x),\quad x\in \mathbb{R}^N\)を考え、初期値\(x\)の解の\(t\)秒後の値を\(\phi (t,x)\)と表すことにします。
\(p\in \mathbb{R}^N\)の\(\omega\)-極限集合(\(\omega\)- limit set)\(\omega(p)\)とは、
\[ \begin{aligned}\omega(p) := \{x\in \mathbb{R}^n \mid \exists \{t_i\}_{i\in \mathbb{N}}\subset \mathbb{R},t_i \to \infty , \lim _{i\to \infty } \phi(t_i,p)= x \}\end{aligned} \]
です。これは正の極限集合とも呼ばれます。
\(\alpha \)-極限集合は、\(t_i \to -\infty\)とすることで同様に定義されます。
例えば、ある平衡解に向かうような点の\(\omega\)-極限集合は、その平衡解のみからなる一点集合です。
\(\omega (p)\)が閉軌道となるとき、それはリミットサイクル(limit cycle)、あるいは極限周期軌道と呼ばれます。(後に例を紹介します)
もしある解が周期軌道に近づいていくとしたら、その解は時間無限大で一点に収束しません。つまり、単に解の極限を取るだけでは長期的な時間の挙動を捉えられないわけです。
そこで、時間の列\(\{t_i\}_{i\in \mathbb{N}}\)という部分列を取って近づける点の集まりを考えれば、極限が周期軌道となるケースを捉えられます。これが\(\omega\)-極限集合の定義のポイントです。
ちなみに、リミットサイクルは、メトロノームなどのリズムを生み出す現象(自励振動現象)の説明に使われています。
参考:リズム現象の物理学 : 基礎・モデリング・生物の話題・ネットワーク関係など(第55回物性若手夏の学校(2010年度),講義ノート) – 郡 宏
極限集合については一般に、次のような性質が知られています。
\(M\subset \mathbb{R}^N\)をコンパクトな正の不変集合とし、\(p \in M\)とする。このとき、\(\omega(p)\)は、空でない閉集合であり、正不変であり、連結である。
不変集合の定義は:不変集合、安定・不安定・中心多様体とは何か?
ポアンカレ・ベンディクソンの定理
ポアンカレ・ベンディクソンの定理は、平面の力学系の\(\omega\)-極限集合がシンプルになることを示しています。
定理(Poincaré–Bendixson)
\(N=2\)とする。\(M\subset \mathbb{R}^2\)をコンパクトな正の不変集合で、有限個の不動点を含むものとする。
\(p \in M\)に対し、\(\omega (p)\)は次のいずれかひとつを満たす。
(i) \(\omega (p)\)は不動点1つ
(ii) \(\omega (p)\)は閉軌道1つ
(iii) \(\omega (p)\)は、有限個の不動点\(p_1 ,\dots,p_n\)と、\(\alpha(\gamma)=p_i\)、\(\omega(\gamma)=p_j\)となる軌道\(\gamma\)から成る。
参考:Wiggins Introduction to Applied Nonlinear Dynamical Systems and Chaos
条件(ii)は先程述べたリミットサイクルとも言いかえられます。
条件(iii)は不動点をつなぐ軌道です。異なる不動点をつなぐ軌道をヘテロクリニック軌道(heteroclinic orbit)、ある不動点から出発しその点へ返ってくる軌道をホモクリニック軌道(homoclinic orbit)と呼びます。
証明の概略は次のとおりです。
もし不動点のみを含むなら、\(\omega(p)\)は仮定より連結で、不動点は有限個なので、それは一点になります。これが(i)。
補題として、\(\omega(p)\)が不動点を含まないなら、\(\omega(p)\)は閉軌道となることが示せます。これを示すためにベクトル場に横断的な(transverse)弧という概念を考え、\(N=2\)という仮定が効いてきます。(横断的な弧と極限集合は、多くても1度しか交わらないことが言える)
つまり、不動点を含まないなら、\(\omega(p)\)は閉軌道となるとなります。これが(ii)です。
残りが、\(\omega(p)\)が不動点とそうでない点を含む場合です。不動点でない点の軌道\(\gamma\)の極限集合\(\omega(\gamma),\alpha(\gamma)\)が、不動点となることを示せば十分です。仮に不動点でないとしましょう。補題より、\(\omega(\gamma),\alpha(\gamma)\)は閉軌道です。しかし、これは\(\omega(p)\)が不動点を含み、連結であることに矛盾します。これで(iii)が示せました。
詳しい証明はWigginsを参照してください。
ポアンカレ・ベンディクソンの定理の応用
ポアンカレ・ベンディクソンの定理を応用すれば、\(\omega(p)\)が閉軌道となる例(リミットサイクル)が存在することを示せます。
\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =x-y – x(x^2+y^2) \\ \frac{dy}{dt} = x+y-y(x^2+y^2) \end{array} \right.\end{aligned} \]
という方程式を考えます。
\(M :=\{ (x,y) \in \mathbb{R}^2 \mid x^2+y^2 \leq 4 \}\)とします。\(M\)は有界閉集合で、ハイネ・ボレルの定理によってコンパクトです。
方程式を極座標変換\(x=r\cos\theta, y = r \sin \theta \)すると、
\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dr}{dt} =r-r^3 \\ \frac{d\theta}{dt} = 1 \end{array} \right.\end{aligned} \]
となります。
\(r>1\)において\(\dot{r} <0\)となるので、\(M\)は正の不変集合です。
そして、\((0,0)\)は唯一の平衡解です。\(\dot {\theta}=1\)なので。
よって、ポアンカレ・ベンディクソンの定理の前提を満たします。
線形化方程式の固有値は\(\lambda = 1 \pm i\)で、実部が正な固有値が存在するので、平衡解\((0,0)\)は不安定です。
参考:線形微分方程式の解の安定性は「固有値」を調べればわかる、微分方程式の安定性を調べる「線形化」の方法とは?
したがって、\(\omega (p) \neq {(0,0)}\)なる点\(p\in M\)が存在します。ポアンカレ・ベンディクソンの定理で、i)もiii)も満たされないので、ii)\(\omega (p)\)が周期解となります。
実際、コンピュータでシミュレーションすると、次のようにリミットサイクルが存在することが見て取れます。
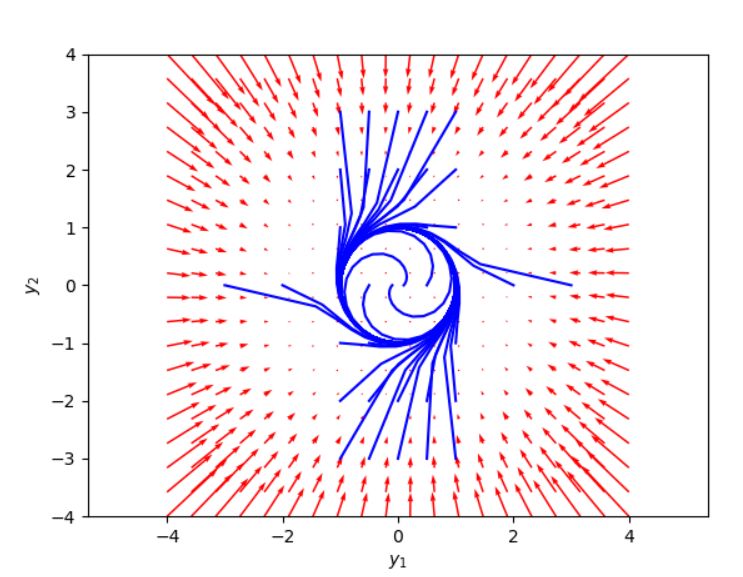
ちなみに、今回はリミットサイクルの存在を示しましたが、平面力学系における閉軌道の非存在を示す定理(Bendixson’s criterion)も知られています。
ポアンカレ・ベンディクソンの定理は、たとえ非線形方程式であっても、解の挙動を詳しく説明する強力な定理です。すなわち、平衡解に向かうか、閉軌道に向かうか、平衡解とそれをつなぐ軌道に向かうか。
ただし、平面の力学系\(N=2\)でしか通用しないことに注意しましょう。平面では閉軌道を「横断する」ことができませんが、3次元以上ではそのような制約がありません。
しかしながら、どのような次元であっても、あるいは偏微分方程式を考えても、極限集合\(\omega (p)\)の考え方は、解の挙動を捉えるために役立つでしょう。
その存在や形状を捉えるのは、まさに解の定性的な挙動を可視化する、力学系らしいアイデアだと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
Introduction to Applied Nonlinear Dynamical Systems and Chaos (Texts in Applied Mathematics)
Springer
売り上げランキング: 16,350
シュプリンガー・フェアラーク東京
売り上げランキング: 1,202,206