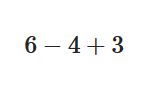どうも、木村(@kimu3_slime)です。
今回は、矩形波のフーリエ級数展開の求め方、ギブス現象とは何かを紹介します。
矩形波とは
矩形波(くけいは square wave)、または方形波(ほうけいは)とは、2つの値を交互に取る次の図のような周期的な関数です。パルス波(pulse wave)とも。
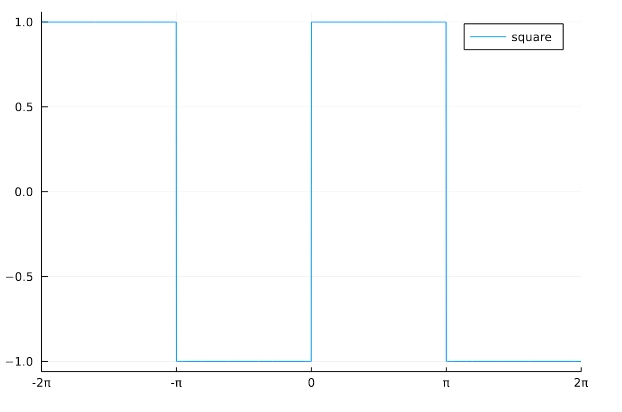
\[ \begin{aligned}f(x)= \begin{cases}1 & (-\pi <x <0 )\\-1 & (0<x <\pi) \\ 0 &(x=-\pi,0,\pi)\end{cases}\end{aligned} \]
という関数を、\(-\pi \leq x \leq \pi\)の外側でも周期的に拡張したもの(\(f(x)= f(x+2n\pi ),n\in \mathbb{Z}\))として定式化できます。
\(x= n\pi\)において、\(f\)は不連続です。上の図では\(f(n\pi)=0\)としています。「2つの値を取る」と説明しましたが、厳密には不連続な点をところどころ持っているわけです。上のグラフはつながっているように(連続でるあるように)見えますが、それはコンピュータの描写の都合で、実際は不連続であることに注意しましょう。
矩形波を表す関数は、
\[ \begin{aligned}f(x)= \mathrm{sgn}(\sin x)\end{aligned} \]
\[ \begin{aligned} \mathrm{sgn}(x)= \begin{cases}1 & (x>0 )\\ -1 &(x < 0) \\ 0 &(x=0)\end{cases}\end{aligned} \]
としても定式化できます。\(\mathrm{sgn}\)はインプットされた数の符号を返す関数です。方形波は、\(\sin \)のような周期的に正負を変える関数から、その符号の部分だけを取り出した関数として見れます。
電気信号、回路によって情報を伝えるには、方形波のようにデジタルな、01的な値を取る波は便利です。例えば、スイッチのオンオフは典型的な不連続な変化と言えます。
音としてのパルス波、ファミコンサウンドも一度聞いてみると体感できて良いでしょう。
矩形波のフーリエ級数展開の求め方、ギブス現象
矩形波は、フーリエ級数展開によって、三角関数の重ね合わせとして表現することができます。
特に今回の設定では、矩形波\(f(x)\)は奇関数なので、フーリエ係数の計算が次のように単純化されます。周期を\(2\pi\)としています。
\[ \begin{aligned}f(x)=\sum_{n=1}^\infty b_n \sin nx\end{aligned} \]
\[ \begin{aligned}b_n = \frac{2}{\pi}\int_0^\pi f(x) \sin nx dx\end{aligned} \]
係数の計算は非常に簡単です。なにしろ、\(f\)が特定の部分である値は一定なのですから。
\[ \begin{aligned} b_n &=\frac{2}{\pi}\int_0^\pi 1 \cdot \sin nx dx \\ &=\frac{2}{\pi}[-\frac{1}{n} \cos nx]_{0}^{\pi} \\ &= \begin{cases}\frac{4}{n\pi}& (nは奇数 )\\0 & (nは偶数)\end{cases} \end{aligned} \]
フーリエ係数、つまり各周波数での三角関数\(\sin n\pi\)の振幅、スペクトルを図示すると次のようになります。
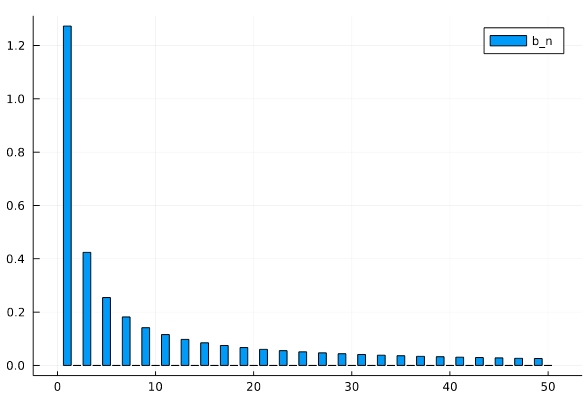
ポイントは偶数番が消えていること、\(\sin x\)の成分が最も大きく、番号が増すにつれ小さくなっていくことですね。
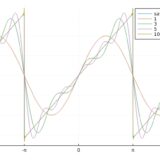
フーリエ級数展開、そのグラフは次の通りです。
\[ \begin{aligned}f(x)=\sum_{k=1}^\infty \frac{4}{(2k-1)\pi} \sin (2k-1)x\\ = \frac{4}{\pi}\sin x+ \frac{4}{3\pi} \sin 3x + \frac{4}{5\pi} \sin 5x +\cdots\end{aligned} \]

基本的に項数を増やすほど、方形波のグラフに近づいているのが見て取れます。方形波のように(区分的になめらかな)不連続な関数でも、フーリエ級数は元の関数に平均収束(\(L^2\)収束)することが知られています。つまり、面積的な(2乗)誤差は限りなく0に近づいていくわけです。
特に不連続点の付近の挙動に注目してみると、\(n=1000\)のグラフであってもトゲのようなもの(ピーク)があります。これは不連続点を持つ関数のフーリエ変換に共通して見られる現象で、ギブス現象(Gibbs phenomenon)と呼ばれるものです。
一般に、関数\(f\)の不連続点\(x=a\)におけるフーリエ級数の値は、左極限と右極限の平均
\[ \begin{aligned}\frac{\lim_{x \nearrow a}f(x)+\lim_{x \searrow a}f(x)}{2}\end{aligned} \]
に収束しています(ディリクレの定理)。方形波ならば、\(\frac{-1+1}{2}=0\)です。そもそも、これに一致するように方形波の不連続点での値を定義しました。しかし、方形波の不連続点での値をどのように設定しようとも、フーリエ級数の不連続点での値は必ず\(0\)に収束します。
フーリエ級数展開から、特定の興味深い級数の値が得られることがあります。例えば、
\[ \begin{aligned}f(x)=\sum_{k=1}^\infty \frac{4}{(2k-1)\pi} \sin (2k-1)x\end{aligned} \]
において、\(x= \frac{\pi}{2}\)としてみると、\(\sin\)の部分は\(1,-1\)のいずれかです。つまり、
\[ \begin{aligned}1 = \sum_{k=1}^\infty \frac{4}{(2k-1)\pi} (-1)^k\end{aligned} \]
\[ \begin{aligned}\sum_{k=1}^\infty \frac{(-1)^{k-1}}{(2k-1)} = \frac{\pi}{4}\\ = 1-\frac{1}{3}+\frac{1}{5}-\cdots\end{aligned} \]
という級数の値が求められました。この交代級数の式は、円周率に関するライプニッツの公式(Leibniz formula for π)と呼ばれています。この式は、アークタンジェントのテイラー展開からも得られるものです。
奇数の逆数の和という単純な級数が、円周率という無理数に収束していくのは面白いですね。
以上、矩形波とは何か、そのフーリエ級数展開の求め方、ギブス現象、ライプニッツの級数について紹介してきました。
矩形波はシンプルな関数でありながら、そのフーリエ級数展開を見るだけでも面白い性質を持っています。計算も簡単なので、ぜひ試してみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
Partial Differential Equations (Graduate Studies in Mathematics)
Amer Mathematical Society (2010-04-02T00:00:01Z)
¥9,531 (中古品)