どうも、木村(@kimu3_slime)です。
今回は、おもり2つのバネの運動方程式(連成振動)とは何か、そのラプラス変換による解き方を紹介します。
おもり2つのバネの運動方程式
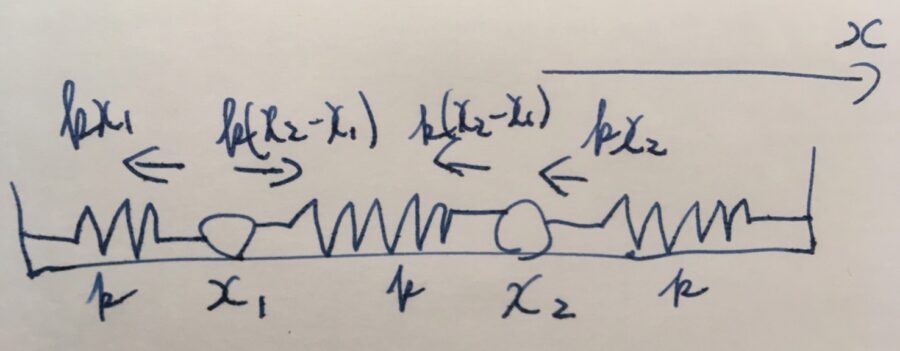
右側を正の向きとして、2つのおもりに働く力を考えましょう。簡単のため、それぞれのおもりの重さは等しく、ばね定数も等しい状況を考えています。
おもり1に働く力は、まず左側のバネから\(-kx_1\)があります。真ん中のバネから力を受けるわけですが、それは真ん中のバネの基準からの変位に依存します。変位は\(x_2-x_1\)なので、\(k(x_2-x_1)\)が真ん中のバネによる力です。結果として、\(F_1 = -kx_1+k(x_2-x_1)\)となります。
おもり2についても同様に考えて、\(F_2 = -k(x_2-x_1)-kx_2\)となります。真ん中のバネによる力の向きに注意しましょう。
以上をまとめて運動方程式を立てると、
\[ \begin{aligned}m \frac{d^2x_1}{dt^2}= -kx_1+k(x_2-x_1)\end{aligned} \]
\[ \begin{aligned}m \frac{d^2 x_2}{dt^2}=-k(x_2-x_1)-kx_2\end{aligned} \]
となりました。
以降では簡単のため、\(m=1\)のケースを考えます。
ラプラス変換による解き方、連成振動
得られた微分方程式を、ラプラス変換によって解いていきましょう。
初期条件を\(x_1(0)=1,\frac{dx_1}{dt}(0)=1\)、\(x_2(0)=1,\frac{dx_2}{dt}=-1\)としたときの解を求めてみます。
\(L(f^{\prime \prime}) = s^2 L(f) -sf^{\prime}(0)-f^{\prime \prime}(0)\)を使うと、
\[ \begin{aligned}s^2L(x_1)-s-1\\= -kL(x_1)+k(L(x_2)-L(x_1))\end{aligned} \]
\[ \begin{aligned}s^2L(x_2)-s+1\\=-k(L(x_2)-L(x_1))-kL(x_2)\end{aligned} \]
で、整理すると
\[ \begin{aligned}(s^2+2k)L(x_1)-kL(x_2)=s+1\end{aligned} \]
\[ \begin{aligned}-kL(x_1)+(s^2+2k)L(x_2)=s-1\end{aligned} \]
となります。さらにこれを解けば、
\[ \begin{aligned}(s^2+2k – \frac{k^2}{s^2+2k})L(x_1)\\=s+1+k\frac{s-1}{s^2+2k}\end{aligned} \]
\[ \begin{aligned}(s^2+2k – \frac{k^2}{s^2+2k})L(x_2)\\=s-1+k\frac{s+1}{s^2+2k}\end{aligned} \]
\[ \begin{aligned} L(x_1)&=\frac{(s^2+2k)(s+1)+k(s-1)}{(s^2+2k)^2 – k^2}\\ &=\frac{s^3+s^2+3ks+k}{(s^2+k)(s^2+3k)} \\ &=\frac{s(s^2+3k)+(s^2+k)}{(s^2+k)(s^2+3k)}\\&= \frac{s}{s^2+k} +\frac{1}{s^2+3k}\end{aligned} \]
\[ \begin{aligned} L(x_2)&=\frac{(s^2+2k)(s-1)+k(s+1)}{(s^2+2k)^2 – k^2}\\ &=\frac{s^3-s^2+3ks-k}{(s^2+k)(s^2+3k)} \\ &=\frac{s(s^2+3k)-(s^2+k)}{(s^2+k)(s^2+3k)}\\&= \frac{s}{s^2+k} -\frac{1}{s^2+3k}\end{aligned} \]
となります。三角関数のラプラス変換
\[ \begin{aligned}L(\cos \omega t )= \frac{s}{s^2+\omega^2}\end{aligned} \]
\[ \begin{aligned}L(\frac{1}{\omega }\sin \omega t)= \frac{1}{s^2+\omega^2}\end{aligned} \]
を用いて逆ラプラス変換すれば、
\[ \begin{aligned}x_1=\cos( \sqrt{k}t)+\frac{1}{\sqrt{3k}}\sin(\sqrt{3k} t)\end{aligned} \]
\[ \begin{aligned}x_2=\cos( \sqrt{k}t)-\frac{1}{\sqrt{3k}}\sin(\sqrt{3k} t)\end{aligned} \]
と解が得られました。
それぞれが、周期の短い振動と周期の長い振動の重ね合わせになっています。このような2つおもりとバネの相互作用による振動は、連成振動(coupled oscillation)と呼ばれるものです。
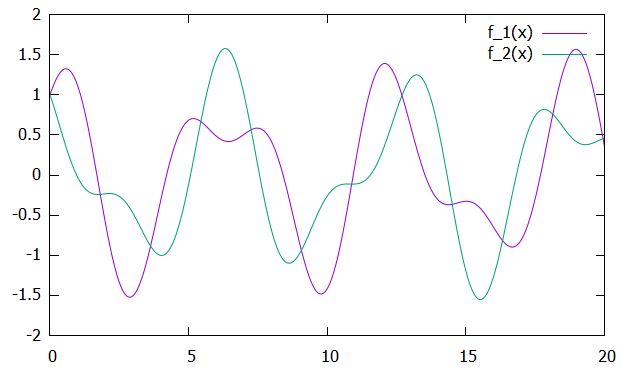
以上、おもり2つとバネの運動方程式を紹介し、その解き方としてラプラス変換を用い、連成振動について紹介してきました。
多少複雑になりますが、連立常微分方程式を解くためにもラプラス変換が使えることがわかりましたね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
おもりバネダンパ系:減衰振動の運動方程式、微分方程式の解き方