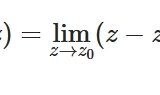三角関数の有理関数の積分：留数定理による計算

どうも、木村（@kimu3_slime）です。

今回は、三角関数の有理関数の積分について、留数定理による計算方法を紹介します。

\(F\)を有理関数（多項式を使った分数関数）として、

\[ \begin{aligned}\int_0 ^{2\pi} F(\cos \theta, \sin \theta) d\theta\end{aligned} \]

と表される積分は、複素解析、留数定理によって計算することができます。

（\(\theta =\tan \frac{x}{2}\)という変換：ワイエルシュトラス置換で実積分としても計算できますが、計算が難しくなることもあります。どちらの手法も知っておいて良いでしょう）

例として、

\[ \begin{aligned}\int_0^{2\pi}\frac{1}{2+\cos \theta} d\theta\end{aligned} \]

という積分を計算してみましょう。

三角関数は、複素の視点で見れば指数関数として見ることができます。\(z=e^{i\theta}\)という変数変換を考えてみましょう。オイラーの公式

\[ \begin{aligned}e^{i\theta}= \cos \theta + i\sin \theta\end{aligned} \]

\[ \begin{aligned}e^{-i\theta}= \cos \theta – i\sin \theta\end{aligned} \]

から、

\[ \begin{aligned}\cos \theta = \frac{z+\frac{1}{z}}{2}\end{aligned} \]

\[ \begin{aligned}\sin \theta = \frac{z-\frac{1}{z}}{2i}\end{aligned} \]

と表されます。したがって、被積分関数は、

\[ \begin{aligned} &\frac{1}{2+\cos \theta}\\ &=\frac{1}{1+(\frac{z+\frac{1}{z}}{2})}\\ &= \frac{2z}{z^2+4z+1} \end{aligned} \]

となります。

また、積分領域は\(\theta : 0 \to 2\pi\)が、\(z\)については\(|z|=1\)の単位円周\(c\)に変わります。変数変換の倍率は、\(\frac{dz}{d\theta} = i e^{i\theta}=iz\)より、\(\frac{d\theta}{dz}= \frac{1}{iz} \)です。よって、

\[ \begin{aligned} & \int_0^{2\pi}\frac{1}{2+\cos \theta} d\theta\\&= \int_{c} \frac{2z}{z^2+4z+1} \frac{1}{iz}dz\\ &= \frac{2}{i} \int_{c} \frac{1}{z^2+4z+1} dz\end{aligned} \]

となります。

ここから留数定理

\[ \begin{aligned}\int_c f(z) dz = 2\pi i \sum_{k=1}^n \underset{z=z_k}{\mathrm{Res}}f(z)\end{aligned} \]

を使って計算しましょう。

\(z^2+4z+1=0\)を解くと、\(z=-2\pm \sqrt{3}\)が得られます。このうち、積分範囲の内部\(|z|<1\)に含まれる孤立特異点は、\(z=-2 +\sqrt{3}\)のみです。外側にある特異点は、積分の結果に影響しないことに注意。

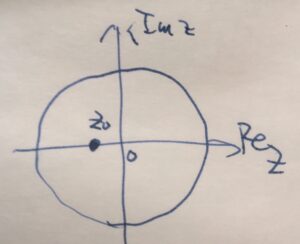
\(z_0 =-2+ \sqrt{3}\)は1位の極なので、極における留数の公式

\[ \begin{aligned}\underset{z=z_0}{\mathrm{Res}}\frac{P(z)}{Q(z)}=\lim_{z \to z_0 }\frac{P(z)}{Q^{\prime}(z)}\end{aligned} \]

を使えば、留数は

\[ \begin{aligned} & \underset{z=z_0}{\mathrm{Res} } \frac{1}{z^2+4z+1}\\&=\lim_{z \to z_0 }\frac{1}{2z+4} \\ &= \frac{1}{2z_0+4} \\ &= \frac{1}{2\sqrt{3}} \end{aligned} \]

です。よって、留数定理から

\[ \begin{aligned} & \int_0^{2\pi}\frac{1}{2+\cos \theta} d\theta\\ &= \frac{2}{i} \int_{c} \frac{1}{z^2+4z+1} dz \\ &=\frac{2}{i} 2\pi i \frac{1}{2\sqrt{3}}\\ &= \frac{2}{\sqrt{3}} \pi\end{aligned} \]

と求められました。

今回の例に限らず、\(z=e^{i\theta}\)の変換によって、三角関数の有理関数の積分は、（複素）有理関数の積分の問題に帰着されます。複素有理関数の積分は、留数定理によって計算できます。

例では積分範囲が\(0<\theta <2\pi\)でしたが、\(0<\theta <L\)であっても同様の手法が使えます。変換後の積分範囲が単位円周となるように、\(z=e^{i \frac{2\pi}{L} \theta}\)とすれば良いわけです。\(\frac{d\theta}{dz}= \frac{L }{2\pi iz}\)となることに注意。

以上、三角関数の有理関数の積分を、留数定理によって計算する方法を紹介してきました。

実積分の計算はしばしば難しくなりますが、複素解析という広い視点から眺めなおすと計算できることがあります。三角関数の有理関数の積分を見たら、留数定理を思い出すと良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。