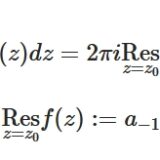極における留数の公式、計算例、位数の求め方

どうも、木村（@kimu3_slime）です。

今回は、極における留数の公式、計算例を紹介します。

極における留数の公式
計算例
こちらもおすすめ

極における留数の公式

そもそも極とは、孤立特異点の一種です。関数\(f\)が\(z=z_0\)を除いて正則であるとき、

\[f(z) =\sum_{n=-\infty}^\infty a_n(z-z_0)^n\]

とローラン展開できますが、その負のべき乗の項

\[ \begin{aligned}\sum_{n=1}^\infty \frac{a_{-n}}{(z-z_0)^n}\end{aligned} \]

を展開の主要部と呼ぶのでした。

そして、主要部が0でなく有限項のとき、孤立特異点\(z_0\)を極と呼びます。また、負のべき乗の最大次数を極の位数と呼びます。

例えば、\(\frac{1}{z(z-1)}\)において、\(z=0,1\)は1位の極です。また、\(\frac{1}{z^2}\)において、\(z=0\)は2位の極です。1位の極は頻繁に登場し、単純な極（simple pole）とも呼ばれます。

ローラン展開における係数\(a_{-1}\)を、\(f\)の\(z=z_0\)における留数\(\underset{z=z_0}{\mathrm{Res}}f(z)\)と呼ぶのでした。

留数は原理的にはローラン展開によって求められるものですが、考えている特異点が極のときは、次のように計算できる公式が知られています。

\(z_0\)が1位の極であるとき

\[ \begin{aligned}\underset{z=z_0}{\mathrm{Res}}f(z)=\lim_{z \to z_0 }(z-z_0)f(z)\end{aligned} \]

2位の極であるとき

\[ \begin{aligned}\underset{z=z_0}{\mathrm{Res}}f(z)=\lim_{z \to z_0 }[\frac{d}{dz}((z-z_0)^2 f(z))]\end{aligned} \]

\(m\)位の極であるとき

\[ \begin{aligned}&\underset{z=z_0}{\mathrm{Res}}f(z)\\&=\frac{1}{(m-1)!}\lim_{z \to z_0 }[\frac{d^{m-1}}{dz^{m-1}}((z-z_0)^m f(z))]\end{aligned} \]

1位の極のケースを考えると、

\[ \begin{aligned}f(z)=\frac{a_{-1}}{z-z_0}+\sum_{n=0}^\infty a_n (z-z_0)^n\end{aligned} \]

となっています。そこで\(z-z_0\)をかければ

\[ \begin{aligned}(z-z_0)f(z)=a_{-1}+\sum_{n=0}^\infty a_n (z-z_0)^{n+1}\end{aligned} \]

で、\(z\to z_0\)の極限を取れば、右辺第二項は0に収束するので、公式が得られました。

一般のケース、\(m\)位の極でも同様の議論ができます。詳しい証明は「Advanced Engineering Mathematics」などを参照してください。

分数関数のときは、次のような計算方法も知られています。

\(P(z),Q(z)\)は正則関数で、\(P(z_0) \neq 0\)で、\(Q(z_0)=0\)で、\(z_0\)は重解ではない（単純な零点）とする。

このとき、分数関数\(\frac{P}{Q}\)において\(z_0\)は1位の極で、

\[ \begin{aligned}\underset{z=z_0}{\mathrm{Res}}\frac{P(z)}{Q(z)}=\lim_{z \to z_0 }\frac{P(z)}{Q^{\prime}(z)}\end{aligned} \]

となる。

\(Q\)を\(z_0\)でテイラー展開すると、\(Q(z)=(z-z_0)Q^{\prime}(z_0)+\sum_{n=2}^\infty a_n(z-z_0)^n\)となります。これを1位の極における留数の公式に当てはめれば、

\[ \begin{aligned}\underset{z=z_0}{\mathrm{Res}}\frac{P(z)}{Q(z)}\\ =\lim_{z \to z_0 }(z-z_0)\frac{P(z)}{(z-z_0)Q^{\prime}(z_0)+\sum_{n=2}^\infty a_n(z-z_0)^n}\\ \ =\lim_{z \to z_0 }\frac{P(z)}{Q^{\prime}(z_0)+\sum_{n=2}^\infty a_n(z-z_0)^{n-1}}\\ =\lim_{z \to z_0 }\frac{P(z)}{Q^{\prime}(z)}\end{aligned} \]

となることがわかりました（\(Q\)は正則なので、導関数は連続）。

計算例

では、留数の公式を使って留数を求めてみましょう。

\(f(z)=\frac{1}{1+z^2}\)の留数を求めます。

\(1+z^2=(z+i)(z-i)\)なので、\(z=i,-i\)が\(f\)の孤立特異点です。また、それらは1位の極です。

極の位数の求め方ですが、多項式分の1\(\frac{1}{Q(z)}\)の形のときは、\(Q\)を因数分解して解が何重解か、ということが位数と一致します。重複のない解なら位数1、二重解なら位数2です。分子が\(z=z_0\)で0になるケースは、分母とキャンセルできるならして、この形に持ち込みましょう。

したがって、1位の極での公式から

\[ \begin{aligned}\underset{z=z_0}{\mathrm{Res}}\frac{1}{1+z^2}\\=\lim_{z \to z_0 }\frac{1}{(1+z^2)^{\prime}}\\ =\frac{1}{2z_0}\end{aligned} \]

\[ \begin{aligned}\underset{z=i}{\mathrm{Res}}f(z)=\frac{1}{2i}\end{aligned} \]

\[ \begin{aligned}\underset{z=-i}{\mathrm{Res}}f(z)=-\frac{1}{2i}\end{aligned} \]

となります。もちろん、極限を使った留数の公式を使って計算しても同じです（試してみてください）。

\(f(z)=\frac{e^{iz}}{1+z^2}\)の特異点、留数を求めましょう。

分母\(e^{iz}\)は複素数全体で正則なので、\(z=\pm i\)が孤立特異点で、それらは1位の極です。さきほどと同様に、1位の極での公式から

\[ \begin{aligned}\underset{z=z_0}{\mathrm{Res}}\frac{e^{iz}}{1+z^2}\\=\lim_{z \to z_0 }\frac{e^{iz}}{(1+z^2)^{\prime}}\\ =\frac{e^{iz_0}}{2z_0}\end{aligned} \]

\[ \begin{aligned}\underset{z=i}{\mathrm{Res}}f(z)=\frac{e^{-1}}{2i}\end{aligned} \]

\[ \begin{aligned}\underset{z=-i}{\mathrm{Res}}f(z)=-\frac{e}{2i}\end{aligned} \]

となります。

最後に、\(f(z)=\frac{z^2}{1-2z+z^2}\)の特異点、留数を求めましょう。

\(f(z)=\frac{z^2}{(z-1)^2}\)であり、\(z=1\)が孤立特異点です。また分母は\(z=1\)で0にならず、分母の重解なので、\(z=1\)は\(f\)の2位の極です。したがって、極における留数の公式から

\[ \begin{aligned}\underset{z=1}{\mathrm{Res}}f(z)\\=\lim_{z \to 1 }[\frac{d}{dz}((z-1)^2 f(z))] \\ = \lim_{z\to 1}[\frac{d}{dz}(z^2)] \\ = \lim_{z\to 1}[2z]\\=2\end{aligned} \]

となることがわかりました。

今回の方法は、特異点が極であるケースにしか使えません。

\(e^\frac{1}{z}\)のように、主要部が無限にある場合：真性特異点における留数は、ローラン展開によって求めることになります。

以上、極における留数の公式、計算例を紹介してきました。

留数定理による積分計算において、問題は留数を求めることに帰着されます。

特異点はどこにあるのか、それは極か、極ならば位数はいくつかを判定し、留数を計算できるようになりましょう。

木村すらいむ（@kimu3_slime）でした。ではでは。