どうも、木村(@kimu3_slime)です。
今回は、ガウス関数のフーリエ変換の計算法として、複素解析、コーシーの積分定理による方法を紹介します。
ガウス関数とは\(f(x)=e^{-ax^2}\)、\(a >0\)のことで、その積分はガウス積分
\[ \begin{aligned}\int_{-\infty} ^{\infty} e^{-ax^2}= \sqrt{\frac{\pi}{a}}\end{aligned} \]
として知られています。
また、実数値関数\(f\)に対し、\(y \in \mathbb{R}\)として
\[ \begin{aligned}\mathcal{F}(f)(y):= \frac{1}{\sqrt{2\pi}} \int _{-\infty} ^\infty f(x) e^{- xyi} dx \end{aligned} \]
を\(f\)のフーリエ変換と呼びます。
今回は、ガウス関数のフーリエ変換がまたガウス関数となること
\[ \begin{aligned}\frac{1}{\sqrt{2a}}e^{-\frac{y^2}{4a}}= \frac{1}{\sqrt{2\pi}} \int _{-\infty} ^\infty e^{-ax^2} e^{- xyi} dx \end{aligned} \]
をコーシーの積分定理を使って示します。
(この結果は、変数変換によって示せることも知られています)
まず、\(y=0\)のとき、等式は成り立っています。
\[ \begin{aligned}\frac{1}{\sqrt{2a}}\cdot 1= \frac{1}{\sqrt{2\pi}} \int _{-\infty} ^\infty e^{-ax^2} \cdot 1dx \end{aligned} \]
は、ガウス積分の結果です。
続いて、実数直線上の積分を計算するために、複素平面上でそれを含むような経路を考えます。\(y>0\)のとき、次のような長方形の経路\(c\)を考えましょう。\(R>0\)を任意の実数とします。\(y<0\)のときも、同様の議論ができます。
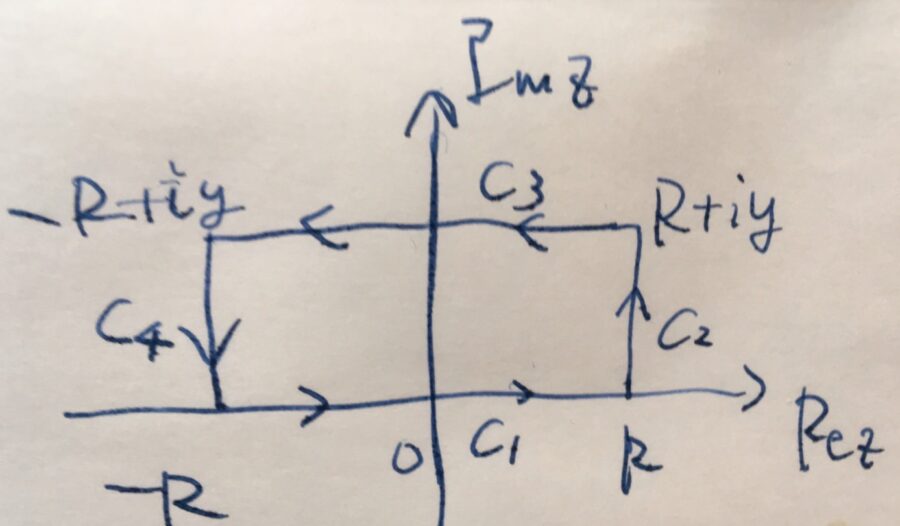
\(f(z)= e^{-az^2}\)は、この長方形領域の内部において正則です。したがって、コーシーの積分定理より、
\[ \begin{aligned}\int_c e^{-az^2}dz =0\end{aligned} \]
です。各直線\(c_1,c_2,c_3,c_4\)ごとに分けて表せば、
\[ \begin{aligned}\int_{c_1} e^{-az^2}dz +\int_{c_2} e^{-az^2}dz +\\ \int_{c_3} e^{-az^2}dz +\int_{c_4} e^{-az^2}dz \\ =0\end{aligned} \]
です。それぞれの直線における積分を計算していきましょう。
実軸上の積分は、
\[ \begin{aligned} & \int_{c_1} e^{-az^2}dz \\&= \int_{-R}^R e^{-ax^2}dx\end{aligned} \]
なので、\(R\to \infty\)でガウス積分\(\sqrt{\frac{\pi}{a}}\)に収束します。
虚軸に並行な直線\(c_2\)における積分は、\(z=ix\)として、\(\frac{dz}{dx}=i\)に注意して
\[ \begin{aligned} & \int_{c_2} e^{-az^2}dz \\&= \int_{0}^y e^{-a(R+ix)^2} i dx\\ &= \int_{0}^y e^{-a(R^2 +x^2)}e^{-2R xi} i dx \end{aligned} \]
となるので、その大きさを三角不等式で評価すると、
\[ \begin{aligned} & |\int_{c_2} e^{-az^2}dz| \\& \leq \int_{0}^y |e^{-a(R^2 +x^2)}e^{-2R xi} i| dx \\ &= \int_{0}^y e^{-a(R^2 +x^2)} dx \\ & \leq\int_{0}^y e^{-a(R^2 +y^2)} dx\\ &= ye^{-a(R^2 +y^2)}\end{aligned} \]
となります。\(y\)は\(R\)に依存していないので、\(R\to \infty\)で積分の大きさは\(0\)に収束します(\(a>0\)という仮定)。横幅\(R\)が大きくなるほど、虚軸方向の積分は\(e^{-az^2}\)の減衰によって小さくなるわけですね。
もう一方の虚軸に並行な経路\(c_4\)での積分も、同様に大きさは\(R\to \infty\)で0です。
また、実軸に並行な経路\(c_3\)での積分は、経路の向きに注意して
\[ \begin{aligned} & \int_{c_3} e^{-az^2}dz \\&= -\int_{-R}^R e^{-a(x+iy)^2}dx\\ &=-\int_{-R}^R e^{-ax^2}e^{-2axyi}e^{ay^2}dx\end{aligned} \]
となります。フーリエ変換の形が現れました。
よって、コーシーの積分定理で得た式において\(R\to \infty\)の極限を取ることで、
\[ \begin{aligned}\sqrt{\frac{\pi}{a}} -\int_{-\infty}^\infty e^{-ax^2}e^{-2axyi}e^{ay^2}dx=0\end{aligned} \]
で、係数を整理して
\[ \begin{aligned}\frac{1}{\sqrt{2a}} e^{-ay^2}=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty e^{-ax^2}e^{-2axyi}dx\end{aligned} \]
となります。ここで、\(y\to \frac{y}{2a}\)と置き直せば、
\[ \begin{aligned}\frac{1}{\sqrt{2a}} e^{-\frac{y^2}{4a}}=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty e^{-ax^2}e^{-xyi}dx\end{aligned} \]
と求めるフーリエ変換が得られました。
特に、\(a= \frac{1}{2}\)のときは、
\[ \begin{aligned} e^{-\frac{y^2}{2}}=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty e^{-\frac{x^2}{2}}e^{-xyi}dx\end{aligned} \]
となり、\(\mathcal{F}(e^{-\frac{x^2}{2}})(y)=e^{-\frac{x^2}{2}}\)となります。これは\(e^{-\frac{x^2}{2}}\)がフーリエ変換\(\mathcal{F}\)の固有値1に対応する固有関数である、とも言えます。
以上、ガウス関数のフーリエ変換の計算法として、コーシーの積分定理を紹介してきました。
複素フーリエ変換の計算には、しばしば複素解析の知識が役立ちます。ガウス関数はフーリエ変換によって形を変えない関数という事実を知ると、貴重なものに思えるのではないでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
Kreyszig, E: Advanced Engineering Mathematics
Wiley John + Sons (2011-05-03T00:00:01Z)
¥10,314 (中古品)
岩波書店 (2003-12-12T00:00:01Z)
¥2,640
日本評論社 (2009-06-01T00:00:01Z)
¥5,170
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740