勾配ベクトルが等位曲面に垂直である（法線ベクトル）：例と証明

どうも、木村（@kimu3_slime）です。

今回は、勾配ベクトルがその等位曲面に垂直であること、法線ベクトルであることについて、例と証明を紹介します。

\(f(x,y,z)\)を微分可能な3変数関数としましょう。\(c\)を実数として、\(f(x,y,z)=c\)を満たす\((x,y,z)\)の集合を、\(f\)の\(c\)における等位曲面、等高面（level surface）と呼びます。

例として、\(f(x,y,z)=x^2+y^2-z\)を考えましょう。\(c=0\)における等位曲面は、\(z=x^2+y^2\)を満たすので、放物曲面になります。\(c=1\)ならば\(z=x^2+y^2-1\)で、\(z\)軸方向に\(-1\)だけ平行移動させた放物曲面ですね。

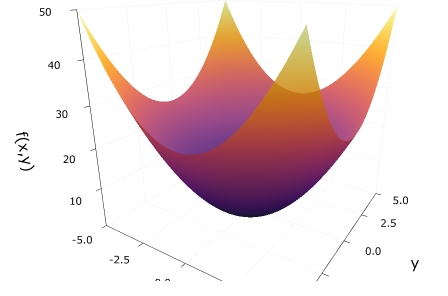
\(f=0\)という等位曲面を考えましょう。その勾配ベクトルは、等位曲面に垂直でしょうか。

勾配ベクトルは、\(\nabla f =(2x,2y,-1)\)です。例えば、原点\(p=(0,0,0)\)における勾配ベクトルは、\(\nabla f(p)=(0,0,-1)\)となります。

原点における接平面は、\(z=0\)を満たす点、すなわち\((x,y,0)\)となります。よって、これらの内積を計算すると、

\[ \begin{aligned}\langle (0,0,-1) , (x,y,0)\rangle =0\end{aligned} \]

となり、確かに垂直であること、接平面の法線ベクトルとなることがわかりました。

以上の議論を一般的にしましょう。

曲面をパラメータ表示するといろいろな曲線\(c_1(t)\)として表せて、その接ベクトル（曲面に接するベクトル）は\(\frac{dc_1}{dt}\)と表せます。

例えば\(f(x,y,z)=x^2+y^2-z\)ならば、\(c_1(t)=(t,t,2t^2)\)は\(t_0=0\)で原点を通る曲面上の曲線のひとつです。\(f(c_1(t))=t^2+t^2-2t^2=0\)を満たすので。接ベクトルは\(\frac{dc_1}{dt}=(1,1,4t)\)で、原点においては\((1,1,0)\)となっていますね。別の曲線として、\(c_2(t)=(t,0,t^2)\)といったものも考えられ、接ベクトルは\((1,0,0)\)です。

曲面上の点\(p\)を通る曲線にはさまざまなものがありますが、それらの接ベクトルが生成する平面が、接平面です。さきほどの例ならば、\((1,1,0),(1,0,0)\)の張る平面、\(\{(x,y,z)\mid z=0\}\)が接平面となっていますね（本当は基底であることを示すために、もう少し議論が必要ですが）。

勾配ベクトルが等位曲面に垂直であるとは、等位曲面の各点\(p\)における接平面に垂直であること、すなわちあらゆる接ベクトルと直交していることと言い換えられます。

\(c_1(t)=(x_1(t),y_1(t),z_1(t))\)を\(p\)を通る曲面上の任意の曲線、すなわち常に\(f(c_1(t))=c\)を満たし、\(c_1(t_0)=p\)を満たす\(t_0\)があるとする。

もし点\(p\)で勾配が0にならない（\(p\)が\(\nabla f(p)\neq 0\)を満たす）ならば、勾配ベクトル\(\nabla f(p)\)は等位曲面の\(p\)における法線ベクトルとなる。すなわち、

\[ \begin{aligned}\langle \nabla f(p),\frac{dc_1}{dt}(t_0)\rangle=0\end{aligned} \]

を満たす。

証明しましょう。

\(f(c_1(t))=c\)を常に満たすので、両辺を\(t\)について微分します。右辺は0です。左辺は合成関数の微分法則（チェインルール）から、

\[ \begin{aligned}\frac{d}{dt}f(c_1(t))\\= \frac{\partial f}{\partial x}\frac{dx_1}{dt}+\frac{\partial f}{\partial y}\frac{dy_1}{dt}+\frac{\partial f}{\partial z}\frac{dz_1}{dt}\\ =\langle \nabla f(c_1(t)),\frac{dc_1}{dt}(t)\rangle\end{aligned} \]

となります。特に\(t=t_0\)のとき、

\[ \begin{aligned}\langle \nabla f(p),\frac{dc_1}{dt}(t_0)\rangle=0\end{aligned} \]

が成り立つことがわかりました。

勾配は0ベクトルでないという仮定ですが、0ベクトルはあらゆるベクトルと直交するので、そういう退化したケースを法線ベクトルとしては扱わないということですね。

逆に今回紹介した性質、「勾配ベクトルに接平面は直交する」を使って、勾配ベクトルから接平面を求めることができます（接平面の定義を勾配ベクトルに直交する平面とすることがある）。

以上、勾配ベクトルが等位曲面に垂直である（法線ベクトル）ことについて、例と証明を紹介してきました。

今回は3次元での議論でしたが、\(n\)次元でも全く同様の議論ができます。

多変数変数を幾何学的に捉えるときに、勾配ベクトルが等位面に直交しているイメージは基本的なので、ぜひ具体的な計算を踏まえて身につけてはいかがでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。