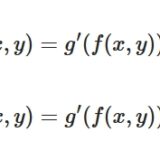どうも、木村(@kimu3_slime)です。
今回は、合成関数の偏微分、チェインルールについて、2次元極座標でのラプラシアンを例に紹介します。
チェインルールとは
簡単なケースでは、合成関数の偏微分は次のように表せます。
チェインルール(連鎖律 chain rule)
\(f:\mathbb{R}^2 \to \mathbb{R}^2\)、\(g: \mathbb{R}^2\to \mathbb{R}\)で、\(f\)は\((x,y)\in \mathbb{R}^2\)において微分可能、\(g\)は\(f(x,y) \in \mathbb{R}\)において微分可能とする。
このとき、合成関数\(g\circ f \)は、\((x,y)\)において偏微分可能で、\(f(x,y)=(f_1(x,y),f_2(x,y))\)とすると、
\[ \begin{aligned}\frac{\partial (g\circ f)}{\partial x } \\ = \frac{\partial g}{\partial x} \frac{\partial f_1}{\partial x}+ \frac{\partial g}{\partial y} \frac{\partial f_2}{\partial x}\end{aligned} \]
\[ \begin{aligned}\frac{\partial (g\circ f)}{\partial y } \\ = \frac{\partial g}{\partial x} \frac{\partial f_1}{\partial y}+ \frac{\partial g}{\partial y} \frac{\partial f_2}{\partial y}\end{aligned} \]
が成り立つ。
変数の部分を省略せずに書けば、
\[ \begin{aligned}\frac{\partial (g\circ f)}{\partial x } (x,y)\\ = \frac{\partial g}{\partial x}(f(x,y)) \frac{\partial f_1}{\partial x}(x,y)+ \frac{\partial g}{\partial y}(f(x,y)) \frac{\partial f_2}{\partial x}(x,y)\end{aligned} \]
となっています。
証明は杉浦「解析入門 Ⅰ」を参照してください。
チェインルールにはより一般的な形もありますが、使ってみて覚えるのが大事だと思います。
2次元極座標でのラプラシアン
\(u(x,y)\)を2回微分可能な2変数関数とします。このとき、2回微分の和
\[ \begin{aligned}\Delta u:= \frac{\partial^2 u }{\partial x^2}+\frac{\partial^2 u }{\partial y^2}\end{aligned} \]
をラプラシアンと呼びます。ラプラシアンを2次元極座標を使って書き表してみましょう。
\[ \begin{aligned}x=r\cos \theta , \quad y = r \sin \theta\end{aligned} \]
と変数変換します。つまり、\(f(r, \theta)=(r\cos \theta ,r\sin \theta)\)と置き、\(u(f(r,\theta)) \)という合成関数の偏微分を求めていきましょう。
まず、1階偏微分を求めると
\[ \begin{aligned} &\frac{\partial u}{\partial r}\\ &=\frac{\partial u}{\partial x} \frac{\partial f_1}{\partial r}+\frac{\partial u}{\partial y} \frac{\partial f_2}{\partial r}\\ &= \cos \theta \frac{\partial u}{\partial x} + \sin \theta \frac{\partial u}{\partial y} \end{aligned} \]
\[ \begin{aligned} &\frac{\partial u}{\partial \theta}\\ &=\frac{\partial u}{\partial x} \frac{\partial f_1}{\partial \theta}+\frac{\partial u}{\partial y} \frac{\partial f_2}{\partial \theta}\\ &= -r\sin \theta \frac{\partial u}{\partial x} + r\cos \theta \frac{\partial u}{\partial y} \end{aligned} \]
となります。
続いて、2階微分を計算しましょう。今度は、\(u\)の偏導関数にチェインルールを適用します。\(u\)の2階偏導関数は連続とは限らない、すなわち偏微分の順序は交換できないものとして議論していきます。
\[ \begin{aligned} &\frac{\partial^2 u}{\partial r^2}\\ &= \frac{\partial}{ \partial r}(\cos \theta \frac{\partial u}{\partial x} + \sin \theta \frac{\partial u}{\partial y})\\ &= \cos \theta \frac{\partial}{ \partial r} (\frac{\partial u}{\partial x}) + \sin \theta \frac{\partial}{ \partial r} (\frac{\partial u}{\partial y})\\ &= \cos \theta (\frac{\partial^2 u}{\partial x^2} \frac{\partial f_1}{\partial r}+\frac{\partial^2 u}{\partial y \partial x} \frac{\partial f_2}{\partial r} )\\ &+ \sin \theta (\frac{\partial^2 u}{\partial x \partial y} \frac{\partial f_1}{\partial r}+\frac{\partial^2 u}{\partial y ^2} \frac{\partial f_2}{\partial r} )\\ &= \cos \theta ( \cos \theta \frac{\partial^2 u}{\partial x^2} +\sin\theta \frac{\partial^2 u}{\partial y \partial x} )\\ &+ \sin \theta ( \cos \theta \frac{\partial^2 u}{\partial x \partial y} +\sin \theta\frac{\partial^2 u}{\partial y ^2} )\\ &= (\cos \theta)^2 \frac{\partial^2 u}{\partial x ^2} +(\sin \theta)^2 \frac{\partial^2 u}{\partial y ^2}\\&+\cos \theta \sin \theta(\frac{\partial^2 u}{\partial y \partial x}+\frac{\partial^2 u}{\partial x \partial y} ) \end{aligned} \]
根気よく、\(\theta\)方向の2階偏微分も計算します。
\[ \begin{aligned} &\frac{\partial^2 u}{\partial \theta^2}\\ &= \frac{\partial }{\partial \theta}(-r\sin \theta \frac{\partial u}{\partial x} + r\cos \theta \frac{\partial u}{\partial y} )\\ &= -r\frac{\partial }{\partial \theta}(\sin \theta \frac{\partial u}{\partial x} )\\&+ r \frac{\partial }{\partial \theta}(\cos \theta \frac{\partial u}{\partial y} )\\ &= -r (\cos \theta\frac{\partial u}{\partial x} +\sin \theta \frac{\partial }{\partial \theta}\frac{\partial u}{\partial x})\\ &+ r(-\sin \theta\frac{\partial u}{\partial y} +\cos \theta \frac{\partial }{\partial \theta}\frac{\partial u}{\partial y} )\\&= -r [\cos \theta\frac{\partial u}{\partial x}\\&+\sin \theta (\frac{\partial^2 u}{\partial x} \frac{\partial f_1}{\partial \theta} +\frac{\partial^2 u}{\partial y \partial x} \frac{\partial f_2}{\partial \theta})]\\& +r [-\sin \theta\frac{\partial u}{\partial y}\\&+\cos \theta (\frac{\partial^2 u}{\partial x \partial y} \frac{\partial f_1}{\partial \theta} +\frac{\partial^2 u}{\partial y^2} \frac{\partial f_2}{\partial \theta})]\\&= -r [\cos \theta\frac{\partial u}{\partial x}\\&+\sin \theta (-r\sin \theta \frac{\partial^2 u}{\partial x} +r\cos \theta\frac{\partial^2 u}{\partial y \partial x} )]\\& +r [-\sin \theta\frac{\partial u}{\partial y}\\&+\cos \theta (-r\sin \theta\frac{\partial^2 u}{\partial x \partial y} +r\cos \theta\frac{\partial^2 u}{\partial y^2} )]\\ &= -r (\cos \theta\frac{\partial u}{\partial x} +\sin \theta\frac{\partial u}{\partial y} )\\&+r^2[(\sin \theta)^2 \frac{\partial^2 u}{\partial x ^2} +(\cos \theta)^2 \frac{\partial^2 u}{\partial y ^2}\\& -\cos \theta \sin \theta(\frac{\partial^2 u}{\partial y \partial x}+\frac{\partial^2 u}{\partial x \partial y})]\\ &= -r \frac{\partial u}{\partial r}\\&+r^2[(\sin \theta)^2 \frac{\partial^2 u}{\partial x ^2} +(\cos \theta)^2 \frac{\partial^2 u}{\partial y ^2}\\& -\cos \theta \sin \theta(\frac{\partial^2 u}{\partial y \partial x}+\frac{\partial^2 u}{\partial x \partial y})] \end{aligned} \]
以上の結果を、うまくキャンセルするようにまとめることができます。
\[ \begin{aligned} & \frac{\partial^2 u}{\partial r^2} + \frac{1}{r^2}\frac{\partial^2 u}{\partial \theta^2}\\ &=[ (\cos \theta)^2 \frac{\partial^2 u}{\partial x ^2} +(\sin \theta)^2 \frac{\partial^2 u}{\partial y ^2}\\&+\cos \theta \sin \theta(\frac{\partial^2 u}{\partial y \partial x}+\frac{\partial^2 u}{\partial x \partial y} )]\\ &-\frac{1}{r}\frac{\partial u}{\partial r}\\&+[(\sin \theta)^2 \frac{\partial^2 u}{\partial x ^2} +(\cos \theta)^2 \frac{\partial^2 u}{\partial y ^2}\\& -\cos \theta \sin \theta(\frac{\partial^2 u}{\partial y \partial x}+\frac{\partial^2 u}{\partial x \partial y})]\\ &= \frac{\partial^2 u }{\partial x^2}+\frac{\partial^2 u }{\partial y^2} -\frac{1}{r}\frac{\partial u}{\partial r}\end{aligned} \]
よって、極座標でのラプラシアンは
\[ \begin{aligned} \Delta u&= \frac{\partial^2 u }{\partial x^2}+\frac{\partial^2 u }{\partial y^2}\\&= \frac{\partial^2 u}{\partial r^2} +\frac{1}{r} \frac{\partial u}{\partial r}+\frac{1}{r^2}\frac{\partial^2 u}{\partial \theta^2}\end{aligned} \]
と求められました。
以上、チェインルールについて、2次元極座標でのラプラシアンを例に紹介してきました。
極座標のラプラシアンは、2次元の円領域におけるラプラス方程式を解くために利用できます。
チェインルールは慣れないうちは複雑ですが、計算するうちに自然と書き下せるようになっていきます。何を変数として何を値とするどんな合成関数の微分をしたいのか、丁寧に手計算してコツをつかんでいきましょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
東京大学出版会 (1980-03-31T00:00:01Z)
¥1,443 (中古品)