どうも、木村(@kimu3_slime)です。
今回は、非線形バネの方程式とは何か、その平衡解の安定性について紹介します。
非線形バネとは
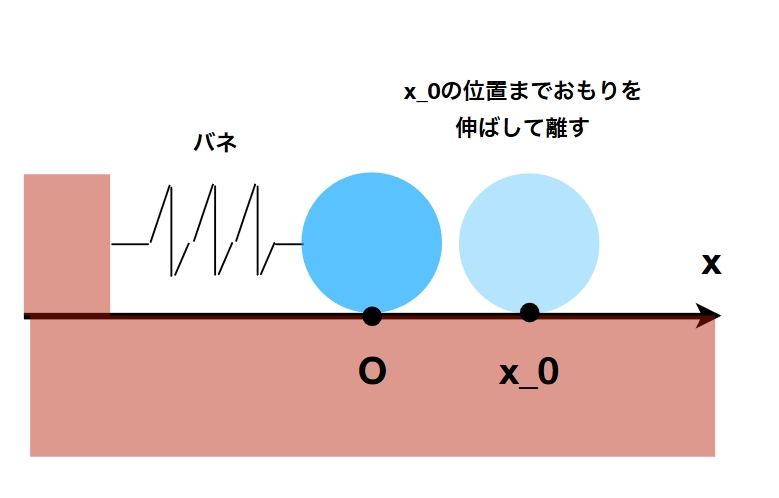
高校物理で学ぶバネは、フックの法則に従い\(F(x)= -kx\)という復元力を持つものです。位置\(x\)に比例して力\(F\)が増えるので、これは線形バネ(linear spring)と呼ばれます。
参考:おもりバネの運動:単振動の運動方程式、微分方程式の解き方
一方で、現実のバネを考えると、位置と復元力が単純な比例関係にないかもしれません。伸ばしすぎると硬くなって復元力が強くなったり、逆に弱くなるかもしれません。そのような復元力\(F(x)\)を、\(x=0\)付近でべき級数展開(テイラー展開)し、
\[ \begin{aligned}F(x)=-kx +ax^2 +bx ^{3}\end{aligned} \]
と3次までの項を使うことにしましょう。さらに、押すときも引くときも同じだけ離れた位置なら同じ大きさ力が働く、つまり奇関数\(F(x)=-F(-x)\)と仮定します。すると、偶数次の係数は\(a=0\)となります。つまり、
\[ \begin{aligned}F(x)= -kx +bx^3\end{aligned} \]
という力を持つバネを考えましょう。これを非線形バネ(nonlinear spring)と呼びます。
運動方程式は
\[ \begin{aligned}m \frac{d^2x}{dt^2} = -kx+bx^3\end{aligned} \]
です。この非線形の微分方程式は、(非減衰の)ダッフィング方程式(Duffing equation)とも呼ばれています。
平衡解の安定性
非線形の微分方程式は、解析的に解くのが難しいです(平均化法)。そこで、平衡解の安定性を調べ、相図を描いてみましょう。
\(x_1 =x,x_2 = \frac{dx}{dt}\)と置くことで、方程式を
\[ \begin{aligned} \frac{dx_1}{dt} &= x_2 \\ \frac{dx_2}{dt}&=-\frac{k}{m}x_1+\frac{b}{m}x_1 ^3 \end{aligned} \]
と連立形に変えられます。その平衡点付近での線形化方程式は
\[ \begin{aligned} \begin{pmatrix}\frac{dx_1}{dt} \\ \frac{dx_2}{dt}\end{pmatrix} &= \begin{pmatrix} 0&1\\ -\frac{k}{m}+\frac{3b}{m}x_1 ^2 &0 \end{pmatrix} \begin{pmatrix}x_1 \\x_2 \end{pmatrix} \end{aligned} \]
です。
\(b\)の正負によって、解の挙動は変わってきます。
硬いバネ
\(b<0\)のとき、\(x\)の増加に対して復元力は大きくなるので、硬いバネ(hard spring)と呼ばれます。
このとき、方程式の平衡解は\((x_1,x_2)=(0,0)\)のみです。線形化方程式は
\[ \begin{aligned} \begin{pmatrix}\frac{dx_1}{dt} \\ \frac{dx_2}{dt}\end{pmatrix} &= \begin{pmatrix} 0&1\\ -\frac{k}{m} &0 \end{pmatrix} \begin{pmatrix}x_1 \\x_2 \end{pmatrix} \end{aligned} \]
となり、線形バネの方程式と同様になります。
行列の固有値は\(\lambda = \pm \sqrt{\frac{k}{m}}i\)と、共役な複素数です。したがって、平衡解はリヤプノフ安定なセンターに分類されます。
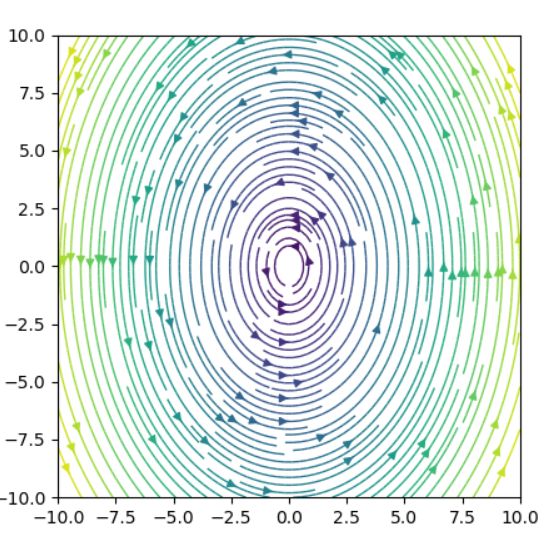
固有値の実部が0のときは、線形化方程式と元の方程式の平衡解付近での挙動は、一般には一致しません。ただし、今回は保存されるエネルギーが存在します。元の方程式
\[ \begin{aligned}m \frac{d^2x}{dt^2} = -kx+bx^3\end{aligned} \]
に\(x\)をかけて積分すれば、
\[ \begin{aligned}\frac{1}{2} m (\frac{dx}{dt})^2 = -\frac{1}{2}kx^2 +\frac{1}{4}bx^4+C\end{aligned} \]
が得られます。\(V(x_1,x_2)=\frac{1}{2} m x_2^2 +\frac{1}{2}kx_1^2 -\frac{1}{4}bx_1^4 \)と置くと、\(V(0,0)=0\)、\(V(x_1,x_2)>0\)、\(\frac{dV}{dt}(x_1,x_2)=0\)なので、\(V\)はリヤプノフ関数の条件を満たします。
よって、もとの非線形方程式においても、\((0,0)\)はリヤプノフ安定です。つまり、線形バネ同様に、周期解が生まれます。

柔らかいバネ
\(b>0\)のとき、\(x\)の増加に対して復元力は小さくなるので、柔らかいバネ(soft spring)と呼ばれます。
このとき、平衡解は複数個存在します。
\((x_1,x_2)=(0,0)\)については、硬いバネと同様です。リヤプノフ関数が存在し、平衡解はリヤプノフ安定です。
他の平衡解として、\(-\frac{k}{m}x_1+\frac{b}{m}x_1 ^3=0\)を解きましょう。すると、\((x_1,x_2)= (\pm \sqrt{\frac{k}{b}},0)\)という平衡解が見つかります。
そこにおける線形化方程式は同じで、
\[ \begin{aligned} \begin{pmatrix}\frac{dx_1}{dt} \\ \frac{dx_2}{dt}\end{pmatrix} &= \begin{pmatrix} 0&1\\ \frac{2k}{m} &0 \end{pmatrix} \begin{pmatrix}x_1 \\x_2 \end{pmatrix} \end{aligned} \]
となります。固有値は\(\pm \sqrt{\frac{2k}{m}}\)で、実部の符号が異なります。よって、平衡解は不安定、サドルに分類されます。
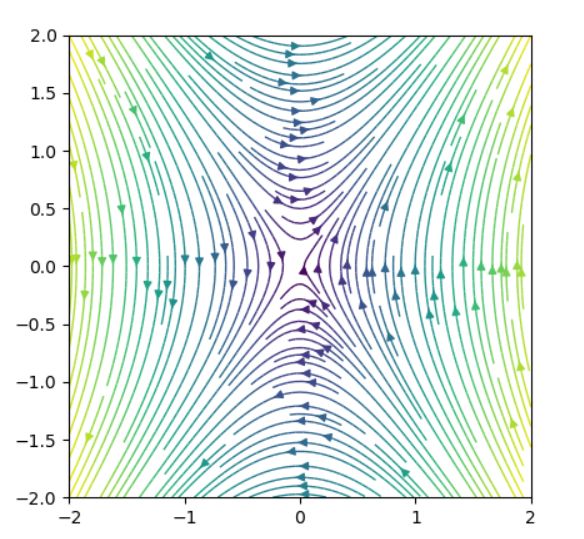
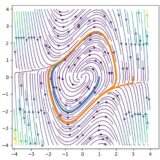
以上の結果をまとめた相図は、次のようになります。原点がセンター、\((x_1,x_2)= (\pm \sqrt{\frac{k}{b}},0)\)がサドルです。

原点付近の解は周期解となって原点付近にとどまりますが、一定以上離れた解は無限遠方へ遠ざかる結果となっていますね。物理的には速度や位置が無限になることはありえず、一定まで増加したときにバネが壊れてしまうでしょう。
より現実的には、バネの力だけでなく減衰力を考慮した方が良いでしょう。その場合、原点は漸近安定となり、より多くの解が原点へと向かうことになります。
以上、非線形バネとは何か、その微分方程式の平衡解の安定性を調べてきました。
この方程式にさらに周期的な外力を加えた方程式は、ダフィング方程式:カオス的な挙動を表す例として有名です。
その簡単なケースとしても、非線形バネの解の挙動がどのようになるか、今回の話で理解してもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
おもりバネダンパ系:減衰振動の運動方程式、微分方程式の解き方