どうも、木村(@kimu3_slime)です。
今回は、2次元線形力学系の平衡点の分類:スパイラル(渦状点)とは何か紹介します。
2次元の線形力学系とは
2次元(平面)の線形力学系とは、\(x(t)=(x_1(t),x_2(t))\)、\(A\)をサイズ\(2,2\)の行列として
\[ \begin{aligned}\frac{dx}{dt}= Ax\end{aligned} \]
と表される連立常微分方程式のことです。
\(Ax=0\)を満たす解、つまり\(x=0\)を平衡解(定常解、固定点、臨界点)と呼びます。
参考:方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門、線形微分方程式の解の安定性は「固有値」を調べればわかる、1次元の線形力学系とは:相図の書き方、安定性
2次元の力学系では、平衡解はおよそ3つに分類されます。
今回はスパイラルについて紹介しましょう。
解の挙動は、行列の固有値によって影響を受けます。行列の成分を
\[ \begin{aligned}A= \begin{pmatrix} a&b\\ c&d \end{pmatrix}\end{aligned} \]
と表すとき、その固有方程式は
\[ \begin{aligned} &\det (\lambda I-A) \\&= \lambda^2 -(a+d)\lambda +(ad-bc)\\ &= \lambda^2 -\mathrm{tr}A \lambda +\det A\\&= 0 \end{aligned} \]
となるので、固有値は
\[ \begin{aligned} \lambda = \frac{\mathrm{tr} A \pm \sqrt{(\mathrm{tr} A) ^2 – 4 \det A}}{2} \end{aligned} \]
となります。

スパイラルとは
2つの固有値が虚数部分を持つとき、平衡解はスパイラル(渦状点 saddle)、フォーカス(focus)であると呼ばれます。
つまり、\((\mathrm{tr} A) ^2 – 4 \det A< 0\)、のケースです。
不安定スパイラル
\[ \begin{aligned}A= \begin{pmatrix} 1&2\\ -2&1 \end{pmatrix}\end{aligned} \]
のとき、固有値は\(1\pm 4i\)で、対応する固有ベクトルは\((1,2i),(1,-2i)\)です。実固有ベクトルは存在しません。
固有値の実部が正なので、平衡点は不安定です。これは不安定なスパイラル(unstable spiral)と呼ばれます。
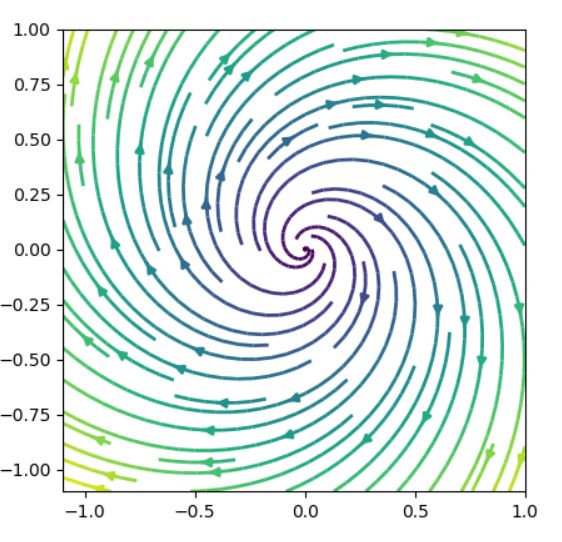
解曲線を求めてみましょう。微分方程式の1本目の式に\(x_1\)をかけると、\(x_1 \frac{dx_1}{dt} =x_1^2+2x_1x_2\)です。2本目の式に\(x_2\)をかけて、\(x_2 \frac{dx_2}{dt} =-2x_1x_2+x_2^2\)。これらを足せば、\(x_1 \frac{dx_1}{dt}+x_2 \frac{dx_2}{dt}=x_1^2+x_2^2\)です。
ここで極座標として、\((r(t))^2=x_1^2+x_2^2\)としましょう。両辺を\(t\)について微分すれば、\(2r \frac{dr}{dt} =2(x_1 \frac{dx_1}{dt}+x_2 \frac{dx_2}{dt})\)です。したがって、\(\frac{dr}{dt} =r\)。これを解けば、\(r= C e^{t}\)という対数螺旋が得られました。
安定スパイラル
\[ \begin{aligned}A= \begin{pmatrix} -2&1\\ -1&-2 \end{pmatrix}\end{aligned} \]
のとき、固有値は\(-2\pm 2i\)で、対応する固有ベクトルは\((1,2i),(1,-2i)\)です。実固有ベクトルは存在しません。
固有値の実部がともに負なので、平衡点は漸近安定です。これは安定なスパイラル(unstable spiral)と呼ばれます。
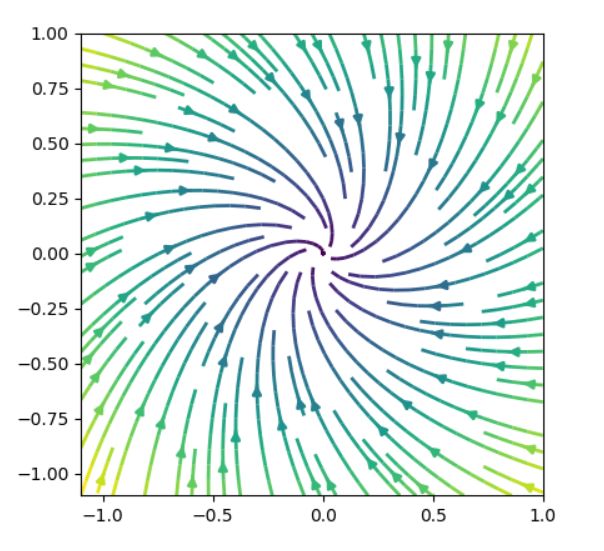
さきほどと同様の議論で、解曲線を求めてみます。\(x_1 \frac{dx_1}{dt}+x_2 \frac{dx_2}{dt}=-2(x_1^2+x_2^2)\)から、\(\frac{dr}{dt} =-2 r\)。これを解くと\(r(t) = Ce^{-2t}\)という対数螺旋が得られます。
センター(中心点)
\[ \begin{aligned}A= \begin{pmatrix} 0&1\\ -2&0 \end{pmatrix}\end{aligned} \]
のとき、固有値は\(\pm 2\sqrt{2} i\)で、対応する固有ベクトルは\((1,2\sqrt{2}i),(1,-2\sqrt{2}i)\)です。実固有ベクトルは存在しません。
固有値の実部がともに0なので、平衡点は(リヤプノフ)安定です。平衡点に一定以上近づくことも離れることもありません。これはセンター(中心点 center)と呼ばれます。
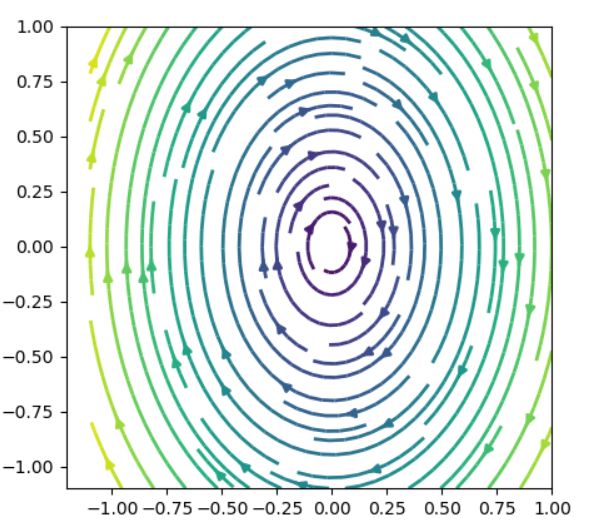
解曲線を求めてみましょう。微分方程式の1本目の式に\(2x_1\)をかけ、2本目の式に\(x_2\)をかけて足せば、\(2x_1 \frac{dx_1}{dt} +x_2 \frac{dx_2}{dt}=0\)が得られます。これを積分すると、\(x_1^2+\frac{1}{2} x_2 ^2 =C\)という楕円の方程式が得られました。
センターは、例えばおもりバネの振動や、振り子の運動方程式において、振幅が小さく周期解となるときに対応しています。
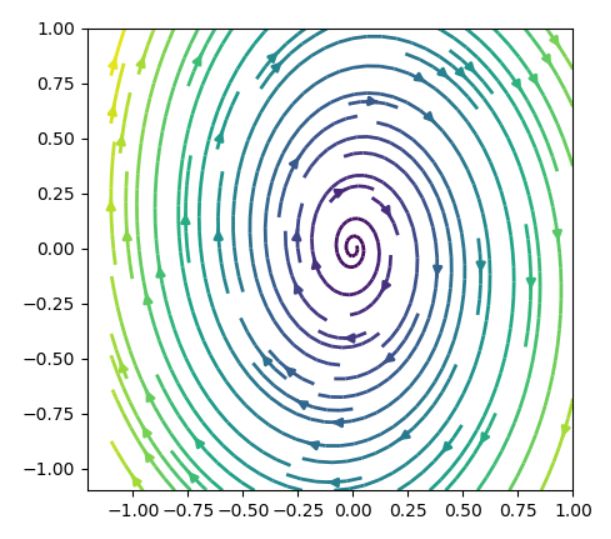
固有値の実部が0の方程式は、ほんの少し形を変えただけで、解の挙動が大きく変わります。例えば、
\[ \begin{aligned}A= \begin{pmatrix} 0.2&1\\ -2&0.2 \end{pmatrix}\end{aligned} \]
は固有値の実部が0でなくなり、不安定なスパイラルです。
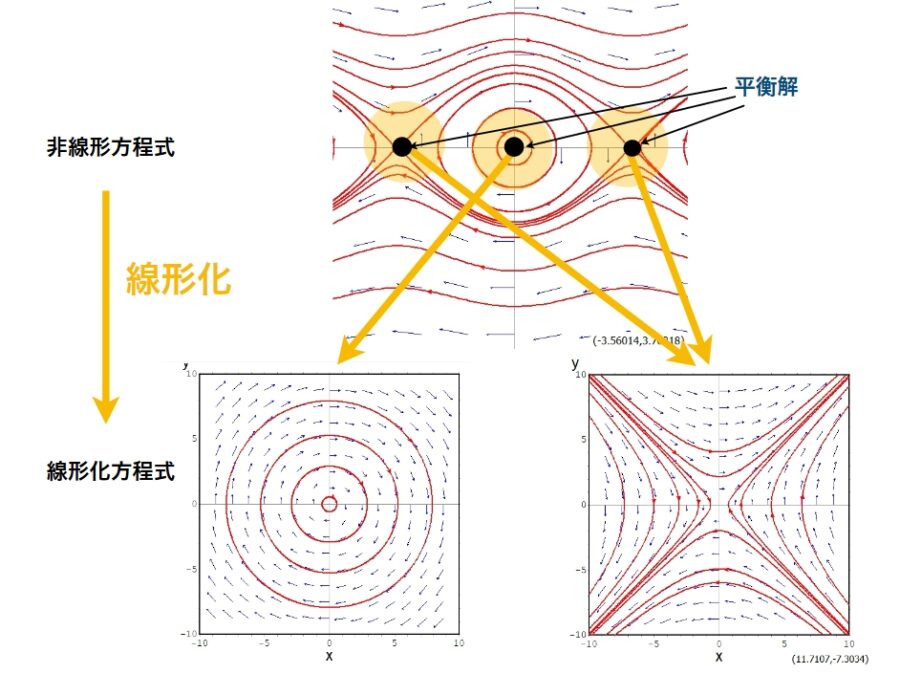
一般に、固有値の実部がすべて0でないとき、平衡点は双曲型(hyperbolic)と呼ばれます。センターは非双曲型の平衡点です。
双曲型の平衡点は、方程式を少し変化させても解の様子が急激に変わることはありえません。しかし、センターがスパイラルに変わるように、非双曲型では大きく変わることがあります。
以上、2次元線形力学系の平衡解の分類として、スパイラルについて簡単な例を交えて紹介してきました。
固有値が虚数部分を持つとき、解は回転し、それがスパイラルと呼ばれます。特に固有値の実部が0のケースでは、周期解になって、それはセンターと呼ばれます。
固有値の様子に応じて力学系を分類し、相図、解曲線をすぐにイメージできるようになってみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門
なぜ行列式を学ぶのか? 固有値・固有ベクトルの求め方:固有多項式の定義