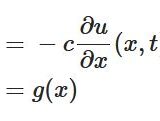どうも、木村(@kimu3_slime)です。
今回は、1次元波動方程式の解、ダランベールの公式を証明、導出を紹介します。
ダランベールの公式とは
考えるのは1次元の波動方程式
\[ \begin{aligned}\frac{\partial^2 u }{\partial t^2}= c^2 \frac{\partial^2 u }{\partial x^2}\end{aligned} \]
の初期値問題
\[ \begin{aligned}u(x,0)=g,u_t (x,0)=h\end{aligned} \]
です。\(x \)の範囲は実数全体\(\mathbb{R}\)です。この問題の解は
\[ \begin{aligned}u(x,t)= \frac{1}{2} \{ g(x+ct) +g(x-ct)\} \\+\frac{1}{2c} \int _{x-ct} ^{x+ct} h(y)dy\end{aligned} \]
と表せます。これがダランベールの公式(d´Alembert’s formula)です。
これは初期値関数が、時間とともに空間両側へ2つの進行波として分かれていくようすを表します。
次の図は、\(u(x,0)=e^{-x^2},u_t (x,0)=0\)のときの解のようすです。
ダランベールの公式の証明
では、証明していきましょう。方針としては、波動方程式をより単純な方程式に帰着させ、それによって解を得ます。
まず方程式を偏微分について整理すると、
\[ \begin{aligned}(\frac{\partial}{\partial t}+c\frac{\partial}{\partial x})(\frac{\partial}{\partial t}-c\frac{\partial}{\partial x})u=0\end{aligned} \]
と積の形に分解できます。そこで、
\[ \begin{aligned}v(x,t):= (\frac{\partial}{\partial t}-c\frac{\partial}{\partial x})u\end{aligned} \]
と置くと、方程式は
\[ \begin{aligned}\frac{\partial v}{\partial t}+c\frac{\partial v}{\partial x}=0\end{aligned} \]
となります。これは1次元の移流方程式(輸送方程式)です。
その解は、\(a(x):=v(x,0)\)と置くとき、
\[ \begin{aligned}v(x,t)=a(x-ct)\end{aligned} \]
と表せます。
この結果と\(v\)の定義式を合わせると、
\[ \begin{aligned} \frac{\partial u}{\partial t}-c\frac{\partial u}{\partial x}=a(x-ct)\end{aligned} \]
となります。これは非同次の移流方程式です。その解は、
\[ \begin{aligned}u(x,t)=g(x+ct)+\int_0^t a(x-ct-c(s-t))ds\end{aligned} \]
と表せることが知られています。
これをダランベールの公式に近づけていきましょう。まず積分の項を整理し、\(x-cs=y\)と置くと、積分範囲は\(x\)から\(x-ct\)、\(\frac{ds}{dy}=- \frac{1}{c}\)なので、
\[ \begin{aligned} u&=g(x+ct)+ \int_0^t a(x-cs)ds \\ &=g(x+ct)+ \frac{1}{c}\int_{x-ct}^x a(y)dy\\ &=g(x+ct)+ \frac{1}{2c}\int_{x-ct}^{x+ct} a(y)dy\end{aligned} \]
となります。
ここで\(a\)を初期条件の言葉で表すと、
\[ \begin{aligned} a(x) &= v(x,0) \\&= \frac{\partial u}{\partial t}(x,0)-c\frac{\partial u}{\partial x}(x,0)\\ &= h(x)-cg^{\prime}(x) \end{aligned} \]
です。これを元の式に戻せば、
\[ \begin{aligned} u&=g(x+ct)+ \frac{1}{2c}\int_{x-ct}^{x+ct} h(y)-cg^{\prime}(y)dy \\ &= g(x+ct)+ \frac{1}{2c}\int_{x-ct}^{x+ct} h(y)dy \\&+\frac{1}{2}[g(y)]_{x-ct}^{x+ct}\\ &= \frac{1}{2} \{ g(x+ct) +g(x-ct)\} \\ &\frac{1}{2c} \int _{x-ct} ^{x+ct} h(y)dy\end{aligned} \]
とダランベールの公式が得られました。
以上、1次元波動方程式の解として、ダランベールの公式の証明、導出を紹介してきました。
この方法が通用するのは1次元のみで、2次元ではポアソンの公式、3次元ではキルヒホッフの公式と呼ばれる解が知られています。より一般的な解法としてはフーリエ級数による解法があります。
1次元の波動方程式では、偏微分をうまく分解して移流方程式に帰着でき、解の挙動もわかりやすい表示式が得られて嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)