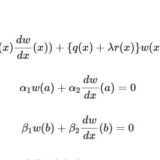移流方程式（輸送方程式）とその解き方を解説

どうも、木村（@kimu3_slime）です。

今回は、移流方程式（輸送方程式）とその解き方を解説します。

移流方程式とは
移流方程式の解き方
移流方程式と波動方程式の共通点、違い
まとめ・発展
こちらもおすすめ

移流方程式とは

風によって暖かい空気が運ばれてくる。煙が風上から流れてきて臭いを感じる。こうした熱や物質が運ばれる現象を、一般に移流と言います。

移流方程式（advection equation）または対流方程式（convection equation）は、水や熱、化学物質などの粒子が、一定の方向へ流される現象を説明する偏微分方程式です。粒子が運ばれる様子を表すことから、輸送方程式（transport equation）とも呼ばれます。

\[\begin{aligned} \frac{\partial u}{\partial t}(x,t)& = -c \frac{\partial u}{\partial x}(x,t)\quad \mathrm{in}\; (0,\infty)\times\mathbb{R} \\ u(x,0)&= u_0(x)\end{aligned} \]

\(u(x,t)\)が、水や熱、化学物質の濃度、密度を表す関数です。一般に、場所\(x\)、時刻\(t\)の変化にともなって変化していきます。

\(c\in \mathbb{R}\)は移動の速度を表す定数で、\(c>0\)なら\(x\)が正の方向へ、\(c<0\)なら負の方向へ解が進みます。\(u_0(x)\)は最初に想定する解の状態、すなわち初期条件を表す関数です。こうした条件下で、方程式を満たす関数\(u\)を見つけるのが、偏微分方程式を解くということですね。

上で書いた方程式は空間1次元ですが、空間\(N\)次元の方程式も同様に考えられます。

\[\begin{aligned} \frac{\partial u}{\partial t}(x,t)& = -c \cdot \nabla u(x,t)\quad \mathrm{in}\; (0,\infty)\times\mathbb{R}^N \\ u(x,0)&= u_0(x)\end{aligned} \]

ここで\(c=(c_1,\dots, c_N)\in \mathbb{R}^N\)は速度ベクトルで、\(\nabla u(x,t)\)は\(u\)の勾配（空間1回偏微分をまとめたベクトル）です。これらの内積は

\[ \begin{aligned}-c \cdot \nabla u(x,t)= -(c_1 \frac{\partial u}{\partial x_1}+ \cdots + c_N \frac{\partial u}{\partial x_N})\end{aligned} \]

と、\(x_k\)軸方向に速度\(c_k\)で移動していることを表すものです。

移流方程式の解き方

1次元の移流方程式を解いてみましょう。

\[\begin{aligned} \frac{\partial u}{\partial t}(x,t)& = -c \frac{\partial u}{\partial x}(x,t)\quad \mathrm{in}\; (0,\infty)\times\mathbb{R} \\ u(x,0)&= u_0(x)\end{aligned} \]

まずは初期条件を忘れて、解の候補を予想してみます。

\(u(x,t)\)について時間1回偏微分、空間1回偏微分と、どちらも1回の偏微分しか登場しないのですから、\(u(x,t)= ax+bt\)という形の関数で置いて、偏微分を計算すればその係数を決められるでしょう。移流方程式に代入すれば、

\[ \begin{aligned}b = -c a\end{aligned} \]

なので、例えば\(u(x,t)= x-ct\)は解の候補です。

このような形の関数で、\(u(x,0)= u_0(x)\)を満たすものを考えると、\(u(x,t)=u_0(x-ct)\)が解であることにたどり着きます。確かに\(t=0\)で条件を満たしますし、合成関数の微分法則から、時間偏微分で\(-c\)が出てくるので方程式を満たします。

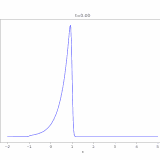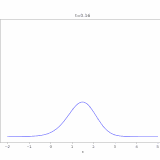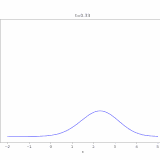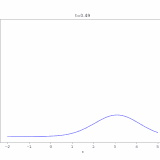
例えば、\(c=1,u_0(x)=e^{-x^2}\)としたときの解\(u(x,t)=e^{-(x-t)^2}\)をコンピュータでアニメ化した図は、次のようになります。

\(t=0\)のときは原点付近にあった関数が、その形を保ったまま、だんだんと\(x\)が正の方向に向かっているのがわかります。速度\(c\)を大きくすればより速く、負にすれば反対側へ進むことは、\(u(x,t)=u_0(x-ct)\)から読み取れますね。

今回は簡単のため1次元の場合を考えましたが、\(N\)次元の場合も、解は\(u(x,t)=u_0(x-ct)\)となることがわかります。

移流方程式と波動方程式の共通点、違い

移流方程式と他の偏微分方程式との関連を見てみましょう。

時間微分、空間微分ともに2回になった方程式は、波動方程式です。

\[\begin{aligned} \frac{\partial^2 u}{\partial t^2}(x,t)& = \Delta u(x,t)\end{aligned} \]

波動方程式の初期値問題\(u(x,0)=g,u_t (x,0)=h\)の解は、

\[ \begin{aligned}u(x,t)= \frac{1}{2} \{ g(x+t) +g(x-t)\} +\frac{1}{2} \int _{x-t} ^{x+t} h(y)dy\end{aligned} \]

と表されることが知られています（ダランベールの公式 ）。例えば、\(u(x,0)=e^{-x^2},u_t (x,0)=0\)のときの解のようすは次のようになります。

参考：波の重ね合わせの原理はなぜ成り立つ？波動方程式入門

移流方程式と比べると、解の形が半分に崩れています。ただし半分に崩れながらも、それぞれの波を別々に見れば、正と負の方向に一定に進んでいるという共通点がありますね。

移流方程式のように1階の偏微分までしか登場しないものは1階の偏微分方程式（first-order PDEs）、波動方程式のように2階の偏微分まで登場するものは2階の偏微分方程式（second-order PDEs）と呼ばれます。

また、移流方程式や波動方程式は共通して、解の挙動が特定の方向性を持っているものでした。これらは、双曲型偏微分方程式（hyperbolic PDEs）に分類されます。

まとめ・発展

今回は、移流方程式とは何か、その解き方、解のようすを紹介してきました。

移流方程式では、解の形が完全に保たれたまま平行移動していきます。ただし、もしインクや熱が流れていくような現象を考えると、単に移流するだけでなく、拡散も同時に起こるはずです。

次のように、移流方程式と拡散方程式（熱方程式）を組み合わせた方程式は、移流拡散方程式（convection–diffusion equation）と呼ばれています。

\[\begin{aligned} \frac{\partial u}{\partial t}(x,t)& = \Delta u-c \cdot \nabla u(x,t)\quad \mathrm{in}\; (0,\infty)\times\mathbb{R}^N \end{aligned} \]

こちらは別記事で紹介するつもりです。

移流方程式は、最もシンプルな偏微分方程式と言えるくらい単純なので、これを理解した上で他の偏微分方程式を学んでいくと良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。