移流拡散方程式、その解き方：熱方程式への関数変換

どうも、木村（@kimu3_slime）です。

今回は、移流拡散方程式とその解き方（解析解）を紹介します。

移流拡散方程式とは
移流拡散方程式の解き方：関数変換
具体例
こちらもおすすめ

移流拡散方程式とは

移流拡散方程式（convection–diffusion equation）は、川に垂らしたインクが流され広がるように、何らかの量\(u(x,t)\)が移流と拡散によって変化する現象を表す偏微分方程式です。

\[\begin{aligned} \frac{\partial u}{\partial t}(x,t)&= \Delta u(x,t)-c \cdot \nabla u(x,t)\quad \mathrm{in}\; (0,\infty)\times\mathbb{R}^N \end{aligned}\]

この方程式は、移流方程式

\[ \begin{aligned} \frac{\partial u}{\partial t}(x,t)& = -c \cdot \nabla u(x,t)\quad \mathrm{in}\;(0,\infty)\times\mathbb{R}^N \end{aligned} \]

と拡散方程式（熱方程式）

\[ \begin{aligned}\dfrac{\partial u}{\partial t}(x,t) &= \Delta u (x,t)\end{aligned} \]

を組み合わせた方程式です。

\(c\)は移流の速さを表すベクトル（定数）で、\(-c \cdot \nabla u(x,t)\)を移流項、\(\Delta u\)を拡散項と呼びます。移流拡散方程式の解の時間変化は、移流と拡散の足し合わせです。

参考：移流方程式（輸送方程式）とその解き方を解説、熱方程式の解き方：変数分離法、フーリエ級数展開（1次元、有界領域）、熱方程式の解き方：フーリエ変換（全空間、N次元）

移流拡散方程式の解き方：関数変換

では、移流拡散方程式の解き方を紹介しましょう。この方程式

\[\begin{aligned} \frac{\partial u}{\partial t}& = \Delta u-c \cdot \nabla u\quad \mathrm{in}\; (0,\infty)\times\mathbb{R}^N \end{aligned} \]

は、関数変換によって次の熱方程式に帰着させることができます。

\[\begin{aligned} \frac{\partial w}{\partial t}& = \Delta w\quad \mathrm{in}\;(0,\infty)\times\mathbb{R}^N \end{aligned} \]

つまり、\(u(x,t)=\varphi(x,t)w(x,t)\)となるような変換の関数\(\varphi\)が見つけられれば良いわけですね。これを探していきます。簡単のため1次元で計算しましょう。

まず、微分を計算すると

\[\begin{aligned} u_t &= \varphi_t w + \varphi w_t \\ u_x &= \varphi_x w + \varphi w_x \\ u_{xx} &= \varphi_{xx} w + \varphi_x w_x \\ & + \varphi_x w_x + \varphi_x w_{xx}\end{aligned} \]

なので、これを\(u\)の方程式に代入して整理します。すると、

\[\begin{aligned} \varphi w_t &= \varphi w_{xx} + (2\varphi_x – c\varphi)w_x\\&+(-\varphi_t + \varphi_{xx} -c \varphi_x)w \end{aligned} \]

となります。これが熱方程式の形であるためには、\(w_x,w\)の係数が常に\(0\)であるように\(\varphi\)を選ぶ必要があります。

\(w_x\)の係数に注目すると、\(\varphi_x = \frac{c}{2} \varphi\)で、これは簡単な常微分方程式です。\(x\)に関する任意の定数を\(\psi (t)\)として、\(\varphi = \psi (t) e^{\frac{cx}{2}}\)と表せます。

この結果を\(-\varphi_t + \varphi_{xx} -c \varphi_x=0\)に代入して、整理しましょう。すると、\(\psi_t=-\frac{c^2}{4} \psi\)と常微分方程式になって、\(\psi=e^{-\frac{c^2}{4}t}\)です（任意定数を1とした）。

これで\(\varphi= e^{(\frac{cx}{2} -\frac{c^2}{4}t)}\)が確かに見つかりました。この変換を行えば、移流拡散方程式は熱方程式になります。

つまり、熱方程式を解いて\(w\)を得てから、\(u(x,t)=e^{(\frac{cx}{2} -\frac{c^2}{4}t)} w(x,t)\)とすれば、移流拡散方程式の解が得られるわけです。この解の挙動は、熱方程式の解\(w\)に、速度\(\frac{c}{2}\)で\(x\)の正の方向へ動かすような要素がかかったものです。確かに、拡散と移流が合わさっていますね。

今回は1次元で計算を行いましたが、一般の次元でも\(\varphi= e^{(\frac{c\cdot x}{2} -\frac{|c|^2}{4}t)}\)と変換すれば、熱方程式に帰着されます。

具体例

では、1次元のときの具体例を見てみましょう。

移流拡散方程式の全空間\(\mathbb{R}\)における初期値問題\(u(x,0)=u_0(x)\)を考えます。

\(u(x,t)=e^{(\frac{cx}{2} -\frac{c^2}{4}t)} w(x,t)\)であり、全空間における熱方程式の解\(w\)は

\[w(x,t) = \frac{1}{\sqrt{4\pi t}} \int_{\mathbb{R}} e^{-\frac{|x-y|^2}{4t}} g(y) dy\]

と表されるのでした。

熱方程式の初期関数\(g\)を\(-1\leq x \leq 1\)で\(1\)、それ以外で\(0\)という値を取る関数としましょう。すると\(u_0(x) \)は\(-1\leq x \leq 1\)で\(e^{(\frac{cx}{2})}\)、それ以外で\(0\)です。

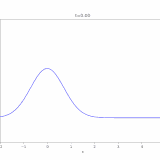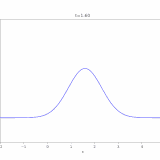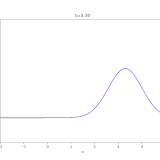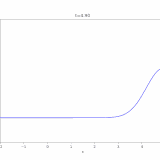
\(c=5\)のとき解\(u\)をコンピュータで描くと、次のようになります。

確かに移流と拡散が起こっていますね。

別の例として、有界領域\((0,1)\)における初期値境界値問題を考えましょう。

初期値を\(u_0(x)=e^{\frac{cx}{2}} \sin \pi x\)、ディリクレ境界条件\(u(0,t)=u(1,t)=0\)とします。インクの濃度変化の例えで言えば、境界ではフィルターによって濃度が0になるようになっているわけです。

このとき、\(w(x,t)= e^{-\pi^2 t}\sin \pi x\)が、対応する境界条件\(w(0,t)=w(1,t)=0\)を満たす熱方程式の解です。よって、もとの方程式の解は\(w(x,t)= e^{(\frac{cx}{2} -\frac{c^2}{4}t)} e^{-\pi^2 t}\sin \pi x\) となります。

\(c=10\)のときに解をコンピュータでアニメ化したのが次の図です。

熱方程式の解では中央に山があるまま減衰していきましたが、移流拡散方程式では解が\(x=1\)側に流されているのがわかります。\(x\)が小さいところは変化が小さく、\(x\)が大きいところでは変化が大きいですね。

今回は、移流拡散方程式とは何か、その解き方を紹介してきました。

関数変換による方法は、温度に応じた減衰のある熱方程式

\[\begin{aligned} \frac{\partial u}{\partial t}(x,t)& = \Delta u(x,t)-bu \quad \mathrm{in}\; (0,\infty)\times\mathbb{R}^N \end{aligned} \]

にも使えます。変換のための関数は\(e^{-\beta t}\)で、移流は起こらず減衰のみが強くなることがわかります。

よく知らない偏微分方程式の解き方を考えるとき、何らかの変換によって、解法がわかっている偏微分方程式や常微分方程式に帰着させるのは、多くの問題で役立つ基本的な考え方ですね。

木村すらいむ（@kimu3_slime）でした。ではでは。