どうも、木村(@kimu3_slime)です。
今回は、ロトカ・ヴォルテラ系の平衡解の安定性、解曲線の求め方を紹介します。
ロトカ・ヴォルテラ方程式とは、
\[ \begin{aligned}\frac{du}{dt}= au – buv \\\frac{dv}{dt}= cuv – dv\end{aligned} \]
と表される非線形の連立常微分方程式です。\(a,b,c,d>0\)は定数です。
\(u\)はウサギのような被食者(餌)、\(v\)はキツネのような捕食者を表すモデル(被食者-捕食者モデル)として利用されています。
モデルについて:食う-食われるの数学:捕食者-被食者モデル(ロトカ・ヴォルテラ方程式)とは?
ロトカ・ヴォルテラ方程式の平衡解を求めてみましょう。つまり、
\[ \begin{aligned}au – buv =0\\cuv – dv =0\end{aligned} \]
を解きます。まずひとつとして、\((u,v)=(0,0)\)は平衡解です。\(u ,v\neq 0\)のときを考えると、\((u,v)=(\frac{d}{c},\frac{a}{b})\)が見つかりますね。
それぞれの平衡点で方程式を線形化し、安定性を調べてみましょう。一般的な線形化方程式は
\[ \begin{aligned}\begin{pmatrix} \frac{du}{dt}\\\frac{dv}{dt} \end{pmatrix}&= \begin{pmatrix}\frac{\partial f_1}{\partial u}&\frac{\partial f_1}{\partial v}\\ \frac{\partial f_2}{\partial u} &\frac{\partial f_2}{\partial v}\end{pmatrix} \begin{pmatrix} u\\v\end{pmatrix}\\ &=\begin{pmatrix}a-bv&-bu\\ cv & cu-d\end{pmatrix} \begin{pmatrix} u\\v \end{pmatrix}\end{aligned} \]
となります。
平衡解\((u,v)=(0,0)\)においては、線形化方程式は
\[ \begin{aligned}\begin{pmatrix} \frac{du}{dt}\\\frac{dv}{dt} \end{pmatrix}&= \begin{pmatrix}a&0\\0 & -d\end{pmatrix} \begin{pmatrix} u\\v \end{pmatrix}\end{aligned} \]
となります。
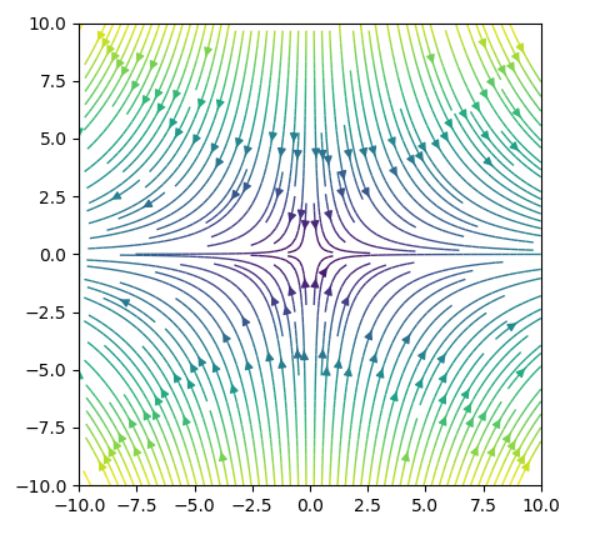
固有値は\(a,-d\)で、符号の異なる実数です。このとき、平衡点は不安定で、サドルと呼ばれます。
\((u,v)=(0,0)\)は被食者と捕食者がいなくなる、絶滅状態を表しますが、この方程式ではそれは不安定な状態となっています。
平衡解\((u,v)=(\frac{d}{c},\frac{a}{b})\)においては、線形化方程式は
\[ \begin{aligned}\begin{pmatrix} \frac{du}{dt}\\\frac{dv}{dt} \end{pmatrix}&= \begin{pmatrix}0&-\frac{bd}{c}\\ \frac{ac}{b} &0\end{pmatrix} \begin{pmatrix} u\\v \end{pmatrix}\end{aligned} \]
となります。
固有値は\(\pm \sqrt{ad} i \)で、実部が0の複素数です。このとき、平衡解はリヤプノフ安定で、センターと呼ばれます。
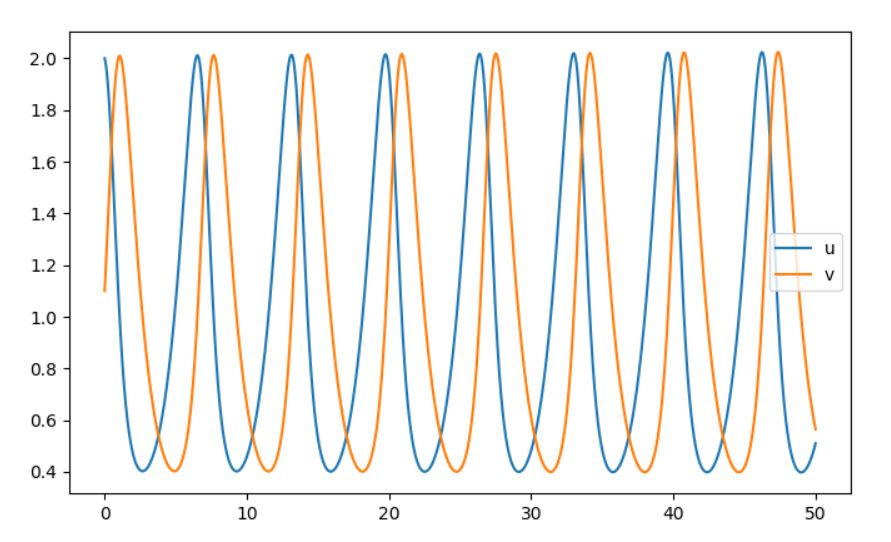
これは被食者と捕食者が共存し、周期的に増減する状態に対応します。
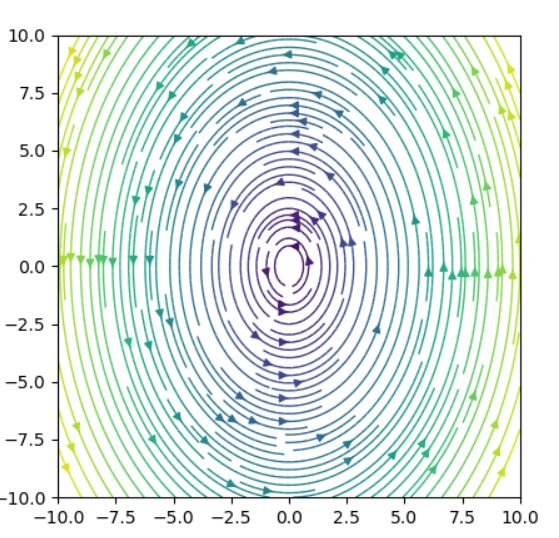
固有値の実部が0のケースでは、厄介なことに、線形化方程式が元の方程式を近似しない可能性があります。
今回は、元の方程式のリヤプノフ関数(保存量関数、エネルギー)を構成することで、その安定性を示すことができます。
\[ \begin{aligned}V(u,v):=-d\log u +cu -a\log v +bv\end{aligned} \]
と置きましょう。
注目している平衡点\((u,v)=(\frac{d}{c},\frac{a}{b})\)において、\(V\)は最小値を取ります。
なぜか。\(u,v\)の関数の部分は独立しているので、1変数関数の最小値を判定すれば良いです。例えば\(f(u)=-d\log u +cu\)とすると、\(f^{\prime}(u) = -d \frac{1}{u}+ c\)なので、\(f^{\prime}(\frac{d}{c})=0\)であり、前後で符号が変化するので、\(u\)についてそこで最小値を取ります。\(v\)についても同様です。
\(u,v\)をロジスティック方程式の解としたとき、\(V(u,v)\)の時間微分は0になることが示せます。
\[ \begin{aligned} \frac{dV}{dt}(u,v) &=\frac{\partial V}{\partial u}\frac{du}{dt}+\frac{\partial V}{\partial v}\frac{dv}{dt}\\ &=(- \frac{d}{u}+ c)(au- buv)\\&+ (- \frac{a}{v}+b)(cuv-dv)\\ &= -ad+bdv+c(au-buv) \\ &-acu+ad+b(cuv-dcv) \\ &=0\end{aligned}\]
したがって、\(V\)はリヤプノフ関数の条件を満たし、\((u,v)=(\frac{d}{c},\frac{a}{b})\)がリヤプノフ安定であることが示せました。(\(\frac{dV}{dt}=0\)となるとき、方程式は保存系と呼ばれる)
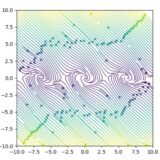
\(C\)を定数として、\(V(u,v)=C\)を満たす\((u,v)\)のなす曲線(等高線)を描いてみましょう。\(V\)は\((u,v)\)が解であるとき、時間変化しない、つまり一定なので、\(V=C\)のなす曲線が解曲線に対応します。
\(V\)は\((u,v)=(\frac{d}{c},\frac{a}{b})\)において最小で、さきほど微分を調べたようにそれぞれの成分について単調増加です。したがって、等高線は閉曲線となり、それが周期解に対応するものです。
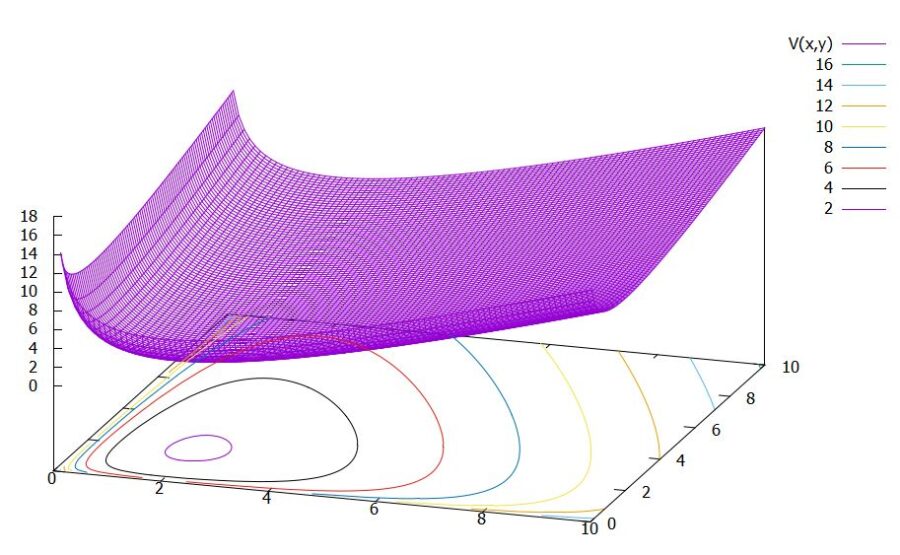
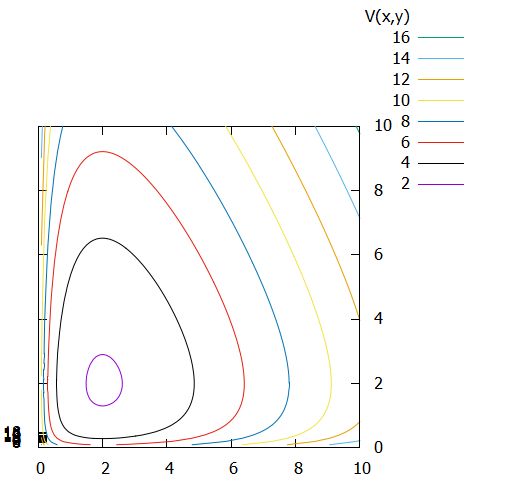
以上の結果をまとめると、ロトカ・ヴォルテラ方程式の相図は次のようになることがわかりますね。
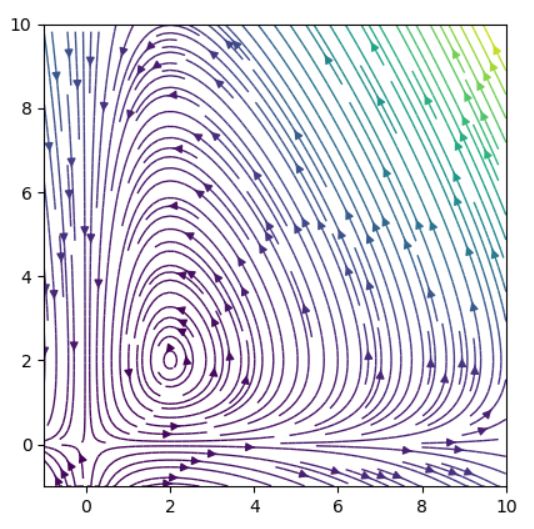
絶滅状態に対応する原点は、不安定なサドルです。共存状態に対応する点は、リヤプノフ安定なセンターで、その付近には周期解があります。
以上、ロトカ・ヴォルテラ方程式の平衡解の安定性、解曲線の求め方を紹介してきました。
このモデルは少し不自然で、捕食者がいないと無限に被食者が増えるようになっています。また、方程式が少しでも変わるとセンターが崩れてしまいます。そこで、安定な周期解(リミットサイクル)が存在するように修正したロトカ・ヴォルテラ方程式を考えることもあるでしょう。
ただ、基本的でシンプルな形の方程式はこれなので、その解の挙動の調べ方について、この記事が参考になれば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
食う-食われるの数学:捕食者-被食者モデル(ロトカ・ヴォルテラ方程式)とは?
方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門