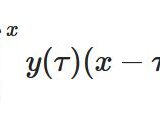畳み込み（合成積）とは：ラプラス変換の性質と導出

どうも、木村（@kimu3_slime）です。

今回は、関数の畳み込み（合成積）とは何か、そのラプラス変換の性質を紹介します。

畳み込みとは
積のラプラス変換
こちらもおすすめ

畳み込みとは

関数\(f,g\)の畳み込み（合成積 convolution）\(f*g\)は、

\[ \begin{aligned}(f*g)(t):= \int_0^t f(\tau)g(t-\tau)d\tau \end{aligned} \]

と定義される積分です。

これはラプラス変換（やフーリエ変換）について

\[ \begin{aligned}L(f*g)= L(f)L(g)\end{aligned} \]

という良い性質（畳み込み定理）を持っているので便利です。

今回は、ラプラス変換の性質について考え、その中で畳み込みの考え方が登場することを紹介します。

積のラプラス変換

ラプラス変換は線形性を持ち、特に関数の和について良い性質を持っています。

\[ \begin{aligned}L(f+g)=L(f)+L(g)\end{aligned} \]

これを使えば、例えば部分分数分解によって、逆ラプラス変換を行うのも簡単です。バラして計算できるので。

しかし、関数の積\(fg(x):= f(x)g(x)\)については保存されません。一般に、

\[ \begin{aligned}L(fg)= L(f)L(g)\end{aligned} \]

が成り立つとは限りません。例えば、\(f(t)=1\)、\(g(t)=t\)とすると、

\[ \begin{aligned}L(fg)= L(g)=\frac{1}{s^2}\end{aligned} \]

\[ \begin{aligned}L(f)=\frac{1}{s}\end{aligned} \]

\[ \begin{aligned}L(g)= \frac{1}{s^2}\end{aligned} \]

なので、\(L(fg)\neq L(f)L(g)\)です。

それでも、\(L(f)L(g)= L(h)\)となるような関数\(h\)が、\(f,g\)が決まっていたら便利ですね。それは次のようにして実際に見つけることができます。

\[ \begin{aligned} L(f)L(g) &= \int_0^\infty e^{-s\tau}f(\tau) d\tau \int_0^\infty e^{-su}g(u) du \end{aligned} \]

ですが、\(u=t-\tau\)と置換してみましょう。積分範囲は\(t:\tau \to \infty\)です。

したがって、フビニの定理（積分の順序交換）により

\[ \begin{aligned} & \int_0^\infty e^{-s\tau}f(\tau) d\tau \int_0^\infty e^{-su}g(u) du \\&= \int_0^\infty e^{-s\tau}f(\tau) d\tau \int_\tau ^\infty e^{-s(t-\tau)}g(t-\tau) dt \\ &= \int _0^\infty f(\tau) (\int_\tau ^\infty e^{-st}g(t-\tau) dt) d\tau \end{aligned} \]

となります。ここで積分領域は\(\{(\tau,t)\mid \tau \geq 0, \tau \leq t \}\)であることに注意して、\(t,\tau\)の順序交換を行うと、

\[ \begin{aligned} & \int _0^\infty f(\tau) (\int_\tau ^\infty e^{-st}g(t-\tau) dt) d\tau \\&= \int _0^\infty e^{-st} (\int_0 ^t f(\tau) g(t-\tau) d\tau) dt \\ &= L(f*g) \end{aligned} \]

と畳み込みの形が表れることがわかりました。

畳み込み積の意味は、一方の関数\(g(t-\tau)\)を移動させながら積を取って積分することです。簡単な関数で計算し、グラフを書いてみると理解しやすいでしょう。

ただ、なぜ畳み込みなんて計算するのだ、畳み込みの定義そのものの意味は何なのだ、と考えるとわかりにくい気がします。

\(L(f)L(g)=L(?)\)という形で計算するのは便利ですが、\(L(f)L(g)=L(fg)\)は一般に成り立たず、\(L(f)L(g)= L(f*g)\)が成り立つ。だから畳み込みは便利だし考えたい、という順序で良いのではないでしょうか。（他にも、畳み込みは良い性質を持っています）

（回路理論や制御理論においては、応答＝アウトプットは、入力＝インプットとインパルスの畳み込みによって表せることが知られています。これによって畳み込みの意味を説明することもあるでしょう。）

例えば、\(\frac{1}{(s^2+\omega^2)^2}\)の逆ラプラス変換を求めたいとしましょう。

そして、\(L(\frac{1}{\omega}\sin \omega t)=\frac{1}{s^2+\omega ^2}\)と知ってるとします。この知識を使えば、\(L(\frac{1}{\omega}\sin \omega t *\frac{1}{\omega}\sin \omega t) =\frac{1}{(s^2+\omega^2)^2}\)です。

したがって、畳み込み積\(\frac{1}{\omega}\sin \omega t *\frac{1}{\omega}\sin \omega t\)が、求めたい逆ラプラス変換の結果となります。

\[ \begin{aligned} & \frac{1}{\omega}\sin \omega t *\frac{1}{\omega}\sin \omega t \\&=\frac{1}{\omega ^2}\int _0^t \sin \omega \tau \sin \omega(t-\tau)d\tau \\ &=\frac{1}{2\omega ^2}\int _0^t (-\cos \omega \tau +\cos (2\omega \tau-\omega t))d\tau\\&= \frac{1}{2\omega ^2}[-\tau \cos \omega t +\frac{1}{\omega }\sin \omega \tau]_0^t\\&= \frac{1}{2\omega^3}(\sin \omega t-\omega t \cos \omega t )\end{aligned} \]

と求められました。

ラプラス変換の結果が積で表され、積の逆変換の結果を個別に知っているとき、逆変換は畳み込みによって計算できます。

以上、畳み込み（合成積）とは何か、そのラプラス変換の性質と導出を紹介してきました。

ラプラス変換の積を前提とすれば、自然と関数の畳み込みの概念にたどり着くと思います。もし畳み込みの意味や定義に納得できなかったら、今回の話が参考になると嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。