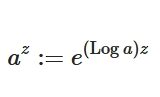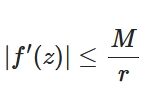コーシーの積分公式とは、計算例と応用（無限回微分可能、コーシーの不等式）

どうも、木村（@kimu3_slime）です。

今回は、コーシーの積分公式とは何か、その計算例と応用を紹介します。

コーシーの積分公式、計算例
応用
こちらもおすすめ

コーシーの積分公式、計算例

コーシーの積分公式（Cauchy’s integral formula）は、正則関数のある点での値は、その点を囲む閉曲線上での関数の値と関係がある、という定理です。

\(f\)を単連結な領域\(D\)において正則な関数とする。\(z_0 \in D\)を任意の点、\(c\)を\(z_0\)を囲む\(D\)内の任意の単純閉曲線とする。このとき、

\[ \begin{aligned}\int_c \frac{f(z)}{z-z_0} =2\pi i f(z_0)\end{aligned} \]

\[ \begin{aligned} f(z_0) =\frac{1}{2\pi i}\int_c \frac{f(z)}{z-z_0}dz \end{aligned} \]

が成り立つ。

仮定は「分母が」正則であることで、被積分関数\(\frac{f(z)}{z-z_0}\)自体は\(z_0\)で正則でないことに注意しましょう。正則な関数の閉曲線での積分は0ですが（コーシーの積分定理）、分母に特異性がある場合は0でなくなる、というのが今回の結果です。正則でない関数の積分が、ある程度簡単に求められます。

この公式と関連付けて覚えておきたい基本的な簡単な結果は、\(\frac{1}{z}\)の単位円周に置ける線積分が

\[ \begin{aligned} \int_c \frac{1}{z}= 2\pi i \end{aligned} \]

となることです。これはコーシーの積分公式において、\(f(z)=1\)、\(z_0=0\)のケースに対応しています。逆に言えば、この結果を一般化したものがコーシーの積分公式というわけです。

分母が0になる\(z=z_0\)、特異性を持つ点での値が、\(2\pi i\)倍されて出てくる、という不思議な結果です。

コーシーの積分公式を使えば、\(f(z)/(z-z_0)\)の形の線積分が簡単に求められます。

例えば、

\[ \begin{aligned} \int_c \frac{e^z}{z-1}dz\end{aligned} \]

を求めてみましょう。以降、\(c\)は分母が0となる点を囲む単純閉曲線とします。

コーシーの積分公式に当てはめるには、\(f(z)=e^{z}\)、\(z_0=1\)と見ればよいです。したがって、

\[ \begin{aligned} \int_c \frac{e^z}{z-1} dz&= 2\pi i f(1) \\ &= 2\pi ei \end{aligned} \]

となります。ちなみに、\(z_0=1\)を含まない単純閉曲線でのこの関数の積分は、0です（コーシーの積分定理）。

もう一つ、

\[ \begin{aligned}\int_c \frac{\mathrm{Log\, }z}{z+i}dz \end{aligned} \]

を求めてみましょう。\(\mathrm{Log\, }z\)は対数関数の主値です。

この関数は0と負の実部で正則ではないので、\(D\)、\(c\)はそこを避けたものとして選ぶことに注意しましょう。例えば、\(z_0 =-i\)を囲む半径\(1/2\)の円盤とすれば良いわけです。すると、\(\mathrm{Log\,}z\)はそこで正則です。

また、対数関数の主値の定義から、\(-i\)の絶対値は\(1\)、偏角の主値は\(-\frac{\pi}{2}\)なので、\(\mathrm{Log\,}(-i)= \log 1 -\frac{\pi}{2}i= -\frac{\pi}{2}i\)となります。よって、コーシーの積分定理から

\[ \begin{aligned} \int_c \frac{\mathrm{Log\, }z}{z+i}dz &= 2\pi i \mathrm{Log\,}(-i) \\ &=2\pi i (-\frac{\pi}{2}i)\\&= \pi ^2\end{aligned} \]

と求められました。

証明について軽く触れましょう。積分を

\[ \begin{aligned} &\int_c \frac{f(z)}{z-z_0}dz \\&= f(z_0)\int_c \frac{1}{z-z_0}dz+\int_{c}\frac{f(z)-f(z_0)}{z-z_0}dz\end{aligned} \]

と分解します。すると、第一項はさきほど紹介した計算から、\(2\pi i f(z_0)\)となります。残りは、第二項の値が0となることを、示せば良いです。コーシーの積分公式（積分路の変形）を使って、\(z_0\)を囲むごく小さな円周での積分に変えられて、\(f\)は連続なので\(f(z)-f(z_0)\)を限りなく小さくすることができます。詳しくは、「Advanced Engineering Mathematics」を参照してください。

応用

コーシーの積分公式は、重要な応用を幅広く持っています。

公式を\(f\)の値という立場から見ると、

\[ \begin{aligned} f(z_0) =\frac{1}{2\pi i}\int_c \frac{f(z)}{z-z_0}dz \end{aligned} \]

となりますが、もし両辺を\(z_0\)を変数として微分することができたら、

\[ \begin{aligned}f^{\prime}(z_0) = \frac{1}{2\pi i} \int_c \frac{f(z)}{(z-z_0)^2}dz \end{aligned} \]

とならないでしょうか。この予想は実際正しく、

\[ \begin{aligned}f^{\prime}(z_0) = \frac{1}{2\pi i} \int_c \frac{f(z)}{(z-z_0)^2}dz \end{aligned} \]

\[ \begin{aligned}f^{(n)}(z_0) = \frac{n!}{2\pi i} \int_c \frac{f(z)}{(z-z_0)^{n+1}}dz \end{aligned} \]

が成り立つことが知られています。

\(f\)が1回複素微分と仮定するだけで、何回でも微分できること、無限回可能であることをこの式から導けます。1回微分可能の仮定だけで無限回可能と言えるのは、実関数とは全く違う状況です。

また、\(c\)を半径\(r\)、\(z_0\)中心の円周としたときの積分公式から、

\[ \begin{aligned}|f^{(n)}(z_0)| \leq \frac{n! M}{r^n}\end{aligned} \]

\[ \begin{aligned}M= \max _{z\in c} f(z)\end{aligned} \]

というコーシーの不等式（Cauchy’s inequality）が得られます。

これはさきほどの結果から、簡単に確かめられるものです。

\[ \begin{aligned} &|f^{(n)}(z_0) |\\&= |\frac{n!}{2\pi i}| | \int_c \frac{f(z)}{(z-z_0)^{n+1}}dz| \\& \leq\frac{n! M}{2\pi } \int_c| \frac{1}{(z-z_0)^{n+1}} |dz \\&= \frac{n! M}{2\pi } \int_c \frac{1}{r^{n+1}}dz \\ &= \frac{n! M}{2\pi } \frac{2\pi r}{r^{n+1}} \\ &= \frac{n! M}{r^n}\end{aligned} \]

と成り立つことがわかりました。

今回は、コーシーの積分公式とは何か、その計算例と応用を紹介してきました。

さらなる応用として、リウヴィルの定理と代数学の基本定理、正則関数のべき級数展開・ローラン展開（留数定理）などがあります。

コーシーの積分公式と合わせて、正則関数にまつわる便利で面白い結果として扱えるようになると良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。