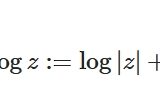複素数の複素数乗、べき乗・指数関数の主値とは何か、計算例

どうも、木村（@kimu3_slime）です。

今回は、複素数の複素数乗、べき乗・指数関数の主値とは何か、計算例を交えて紹介します。

前提知識：複素対数関数の主値Log zとは、計算例

複素べき乗・指数関数の主値とは

実数の一般的なべき乗・指数関数の定義を思い出すと、\(a^{x}:= e^{(\log_e a) x}\)でした。

ここから類推して、複素数\(a,z\)に対して、

\[ \begin{aligned}a^{z}:= e^{(\log_e a) z}\end{aligned} \]

と定義したいのですが、少し注意点があります。

それは、複素対数関数は、一般には多価関数となってしまうことです。

例えば、\(e^{z}=1\)という方程式には、\(z=0,2\pi i, -2\pi i\)など無数の解があります。素朴に考えると、\(\log 1 =0, 2\pi i, -2\pi i\)と複数の値を取ることになってしまい、\(1^z= e^{0z},e^{2\pi iz},e^{-2\pi iz}\)とべき乗も多価関数になっています。

これでは通常の関数（一価関数）として扱えず不便です。そこで、対数関数の主値

\[ \begin{aligned}\mathrm{Log\,} z := \log |z| + \theta i\\ -\pi<\theta \leq \pi\end{aligned} \]

を利用しましょう。\(\theta\)は\(z\)の偏角の主値です\(\theta = \mathrm{Arg\,}z\)。これは一価関数なので、

\[ \begin{aligned}a^{z}:= e^{(\mathrm{Log \,} a) z}\end{aligned} \]

も一価関数として定義できます。これを複素数のべき乗と呼びます。

練習として、複素数のべき乗をいくつか計算してみましょう。

複素数の無理数乗として、\(i^e\)はどんな値でしょうか。\(i\)の絶対値は\(1\)、偏角の主値は\(\frac{\pi}{2}\)です。したがって、

\[ \begin{aligned}\mathrm{Log \,} i = \log |1| +\frac{\pi}{2} i \\ =\frac{\pi}{2} i\end{aligned} \]

なので、べき乗の定義から

\[ \begin{aligned}i^{e} = e^{(\mathrm{Log \,} i ) e}\\ = e^{\frac{\pi e}{2} i} \\ = \cos (\frac{\pi e}{2}) + i \sin \frac{\pi e}{2}\end{aligned} \]

と求められました。

実数の複素数乗として、\(1^{i}\)はどんな値でしょうか。