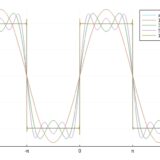
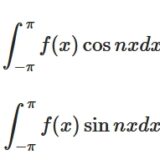フーリエ係数の最良性とは：証明、ベッセルの不等式、パーセバルの等式

どうも、木村（@kimu3_slime）です。

今回は、フーリエ係数の最良性とは何か、その証明、ベッセルの不等式、パーセバルの等式について紹介します。

フーリエ係数の最良性とは
フーリエ係数の最良性の証明
ベッセルの不等式、パーセバルの等式
こちらもおすすめ

フーリエ係数の最良性とは

周期\(2\pi\)の関数\(f\)は、フーリエ級数展開すると

\[ \begin{aligned}f(x)= a_0 +\sum_{n=1}^\infty a_n \cos nx +b_n \sin nx\end{aligned} \]

\[ \begin{aligned}a_0=\frac{1}{2\pi} \int_{-\pi}^{\pi} f(x)dx\end{aligned} \]

\[ \begin{aligned}a_n=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x)\cos nxdx\end{aligned} \]

\[ \begin{aligned}b_n=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x)\sin nx dx\end{aligned} \]

と表すことができます。

これらの係数の決め方が\(f\)を最も良く近似していること、フーリエ係数の最良性について紹介しましょう。

（周期\(2\pi\)としていますが、一般の周期\(2L\)でも同様です。）

つまり、上の係数の決め方とは別に、一般的な係数\(A_n,B_n\)を持った

\[ \begin{aligned}F(x) = A_0 +\sum_{n=1}^\infty A_n \cos nx +B_n \sin nx\end{aligned} \]

という三角級数を考えます。そして、平方誤差

\[ \begin{aligned}E: = \int_{-\pi}^\pi (f(x)-F(x))^2 dx\end{aligned} \]

を考えましょう。\(L^2\)ノルムの言葉を使えば

\[ \begin{aligned}E= \|f-F\|_{L^2}^2\end{aligned} \]

です。そして、\(A_n =a_n ,B_n =b_n\)というフーリエ係数によって決めたときの平方誤差を\(E^{*}\)とします。このとき、

\[ \begin{aligned}E \geq E^{*}\end{aligned} \]

が成り立つこと、つまりフーリエ係数を係数とするときが、\(f\)と三角級数の誤差が最も小さくなることを証明しましょう。

フーリエ係数の最良性の証明

フーリエ係数は無限和ですが、まずは\(N\)項までの有限部分和について、その誤差を計算していきましょう。

さきほどの記法とバッティングしますが、

\[ \begin{aligned}F(x) = A_0 +\sum_{n=1}^N A_n \cos nx +B_n \sin nx\end{aligned} \]

とします。このとき、二乗誤差は

\[ \begin{aligned} &E \\ &= \int_{-\pi}^{\pi} (f(x)-F(x))^2dx \\ &= \int f^2 dx -2\int fFdx+\int F^2 dx\end{aligned} \]

です。最後の2項を計算していきましょう。

積分の線形性、フーリエ係数の定義と三角関数の直交性から、

\[ \begin{aligned} & \int f(x)F(x) dx \\&= \int f( x) (A_0 +\sum_{n=1}^N A_n \cos nx +B_n \sin nx)dx\\ &= \int A_0 f(x) dx +\sum_{n=1}^N (A_n\int f(x)\cos nx dx \\ &+ B_n\int f(x) \sin nx dx )\\ &= \pi(2A_0a_0 +\sum_{n=1}^N(A_n a_n +B_n b_n)) \ \end{aligned} \]

です。また、

\[ \begin{aligned} & \int (F(x))^2 dx \\&= \int (A_0 +\sum_{n=1}^N A_n \cos nx +B_n \sin nx)^2dx\\ &= \int A_0^2 +\sum_{n=1}^N (A_n ^2(\cos nx)^2 \\ &+ B_n ^2 (\sin nx)^2 dx )\\ &= \pi(2A_0^2+\sum_{n=1}^N(A_n ^2 +B_n ^2)) \ \end{aligned} \]

となります。

したがって、

\[ \begin{aligned} E&= \int (f(x))^2 dx \\&-2 \pi(2A_0a_0 +\sum_{n=1}^N(A_n a_n +B_n b_n))\\ &+ \pi(2A_0^2+\sum_{n=1}^N(A_n ^2 +B_n ^2)) \end{aligned} \]

です。\(A_n =a_n,B_n =b_n\)とフーリエ係数として選んだときの誤差\(E^{*}\)を計算すると、キャンセルが起こって

\[ \begin{aligned} E^{*}&= \int (f(x))^2 dx \\&- \pi(2a_0^2 +\sum_{n=1}^N(a_n^2+b_n^2)) \end{aligned} \]

となりました。誤差の差を比較すると、平方完成することができて、

\[ \begin{aligned} &E-E^{*} \\ &=-2 \pi(2A_0a_0 +\sum_{n=1}^N(A_n a_n +B_n b_n)) \\ &+\pi (2A_0^2 +\sum_{n=1}^N(A_n ^2 +B_n ^2) \\ &+2a_0^2 +\sum_{n=1}^N(a_n^2+b_n^2)) \\ &= \pi(2(A_0-a_0)^2+\sum_{n=1}^N (A_N -a_n)^2 \\ & +(B_N -b_n)^2) \geq 0\end{aligned} \]

となりました。実数の2乗は常に正となります。つまり、

\[ \begin{aligned}E \geq E^{*}\end{aligned} \]

は級数展開の係数\(A_n,B_n\)が何であろうが成り立ち、\(A_n =a_n,B_n =b_n\)と選んだときは\(E= E^{*}\)が成り立ちます。

ベッセルの不等式、パーセバルの等式

フーリエ係数を選んだときの二乗誤差に注目すると、興味深い式が得られます。

二乗誤差は常に正なので、\(E^{*} \geq 0\)です。これをさきほどの計算結果と合わせると、

\[ \begin{aligned} 2a_0^2 +\sum_{n=1}^N(a_n^2+b_n^2)\\ \leq \frac{1}{\pi}\int_{-\pi}^{\pi} (f(x))^2 dx\end{aligned} \]

という不等式が得られました。これは極限を取っても成り立ち、

\[ \begin{aligned} 2a_0^2 +\sum_{n=1}^\infty(a_n^2+b_n^2)\\ \leq \frac{1}{\pi}\int_{-\pi}^{\pi} (f(x))^2 dx\end{aligned} \]

ベッセルの不等式（Bessel’s inequality）と呼ばれています。関数の内積、ノルムの言葉を使えば、

\[ \begin{aligned} |\langle f, 1 \rangle _{L^2}|^2 +\sum _{n=1 } ^\infty (|\langle f, \cos nx \rangle _{L^2}|^2 \\ +|\langle f, \sin nx \rangle _{L^2}|^2 )\leq \|f\|_{L^2}^ 2\end{aligned} \]

とも表せます。ベッセルの不等式は、有限次元でも成り立ちます。三角関数は、関数空間において直交していて、したがって線形独立なので、このような不等式が成り立つわけです。

参考：ベッセルの不等式・パーセバルの等式とは：有限のケースで証明

この不等式は、フーリエ係数が減衰することの証明（リーマン・ルベーグの補題）に使えます。（別記事で紹介予定）

実は、フーリエ級数展開ができるならば（\(f\)が二乗可積分\(f\in L^2\)ならば）、ベッセルの不等式においては等号が成り立つことが知られています。つまり、

\[ \begin{aligned} 2a_0^2 +\sum_{n=1}^\infty(a_n^2+b_n^2)\\ = \frac{1}{\pi}\int_{-\pi}^{\pi} (f(x))^2 dx\end{aligned} \]

という等式が得られます。これはパーセバルの等式（Parseval’s identity）と呼ばれるものです。

パーセルバルの等式が成り立つことは、三角関数によって（二乗可積分）関数のフーリエ級数展開ができること（三角関数系の完全性）と同値であることが知られています。

以上、フーリエ係数の最良性とは何か、その証明、ベッセルの不等式、パーセバルの等式について紹介してきました。

この話は知らなくても、フーリエ級数を応用することはできます。しかし、知ることでより視野を広げることができるでしょう。

三角関数で関数を近似しようとしたら、その係数をフーリエ係数として選ぶことが誤差を最も小さくするのです。ベッセルの不等式やパーセルバルの等式は、三角関数系に限らない一般的な式であり、関数解析を学ぶきっかけとして良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。