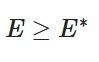フーリエ級数の収束条件：L^2収束、一様収束、不連続点での値

どうも、木村（@kimu3_slime）です。

フーリエ級数の収束条件としては、さまざまなものが知られています。今回は、L^2収束、一様収束、不連続点での値に関する結果を、簡単に解説します。

L^2収束とは
一様収束の十分条件、不連続点での値
こちらもおすすめ

L^2収束とは

今回考えたいのは、

\[ \begin{aligned}f(x)=a_0 + \sum_{n=1}^\infty (a_n \cos \frac{n\pi x}{L} +b_n \sin \frac{n\pi x}{L})\end{aligned} \]

という等式（フーリエ級数展開）は、いつどんな条件で成り立つのかという問題です。

参考：フーリエ係数に関するオイラーの公式の導出

フーリエ級数の収束の一般的な条件として知られているのが、\(L^2\)収束です。

区間\([-L,L]\)において定義された関数\(f\)に対し、有限のフーリエ級数

\[ \begin{aligned}S_N (x):= a_0 + \sum_{n=1}^\infty (a_n \cos \frac{n\pi x}{L} +b_n \sin \frac{n\pi x}{L})\end{aligned} \]

とその極限

\[ \begin{aligned}F(x):= \lim_{N\to \infty} S_N(x)\end{aligned} \]

を考えましょう。\(f\)と\(F\)はどんなときに、どんな意味で一致するのでしょうか。

\(f \in L^2\)（二乗可積分）とする。このとき、フーリエ級数は元の関数に\(L^2\)収束する。

\[ \begin{aligned} \lim_{N\to \infty} \|f-S_N \| _{L^2}=0\end{aligned} \]

\[ \begin{aligned}\|f-S_N \| _{L^2}^2 := \int_{-L}^L |f(x)-S_N(x)|^2 dx\end{aligned} \]

また、（部分列を取ることで、）ほとんど至る所で\(f(x)=F(x)\)が成り立つ。

証明は吉田「ルベーグ積分入門」や黒田「関数解析」を参照してください。

次の図は、矩形波のフーリエ級数展開です。矩形波は不連続な関数であるものの、2乗可積分な関数であり、そのフーリエ級数展開は元の関数に収束します。

\(L^2\)収束は、近似する級数と元の関数との差を、（二乗の）積分によって測った収束です。つまり、項を増やせば増やすほど、もとの関数との面積の違いが限りなく0に近づいていく、というわけですね。\(L^2\)収束（\(L^2\)- convergence）は、平均収束（mean convergence）、平均二乗収束（mean square convergence）とも呼ばれます。

一般に、正規直交な関数系\(\{f_n\}\)は、任意の関数\(f\)を級数として\(f= \sum_{n=1}^\infty a_n f_n\)と表せる時、完全である（complete）と呼ばれます。この言葉を使うと、三角関数によってフーリエ級数展開できることは、三角関数系\(\{1, \cos \frac{n\pi x}{L}, \sin \frac{n\pi x}{L}\}_n\)が（\(L^2\)において）完全性を持つとも言いかえられます。

後半では、「ほとんど至る所で\(f(x)=F(x)\)が成り立つ」という主張がありました。その意味を解説しましょう。

矩形波には、\(x=0,-\pi,\pi\)のように不連続点があります。その点におけるフーリエ級数は、左極限と右極限の平均値に収束し、\(F(0)=0\)となります。これは元の関数の\(x=0\)での値をどのように定義しても、例えば\(f(0)=1\)としても同じです。したがって、その設定のもとでは、\(x=0\)ではフーリエ級数展開と元の関数が一致しません\(F(0)\neq f(0)\)。しかし、そのような不連続な点を除けば一致しているのです。

これを一般的に説明する用語が、「ほとんど至る所で」です。その理解には、測度論、ルベーグ積分論の知識が必要となります。すべて説明すると大変なので、雰囲気だけ紹介しましょう。

\(A=\{0\}\)のような一点集合は、長さとして測ると0になります。このように長さ・測度の値が0となる集合は、測度零集合（measure zero set）と呼ばれます。「ほとんど至る所（almost everywhere, a.e.）で\(f(x)=F(x)\)が成り立つ」とは、ある測度零集合を除いて\(f(x)=F(x)\)が成り立つということです。ほとんどすべての\(x\)について

\[ \begin{aligned}\lim_{N \to \infty} S_N(x) = f(x)\end{aligned} \]

が成り立つことを、\(S_N\)は\(f\)に概収束する（almost everywhere convergence）と呼びます。（一般論として、\(L^p\)収束するならば、概収束する部分列を持ちます。）

矩形波のように、離散的な不連続点を持つ関数について、その不連続点での値は積分の結果に影響しません。そういう点を無視して議論できるのが、\(L^2\)収束や概収束、測度論・ルベーグ積分論の便利なところです。

一様収束の十分条件、不連続点での値

\(f\)に関する仮定がもっと強いと、より強力な収束、一様収束が得られます。

次の図は、三角波のフーリエ級数展開です。

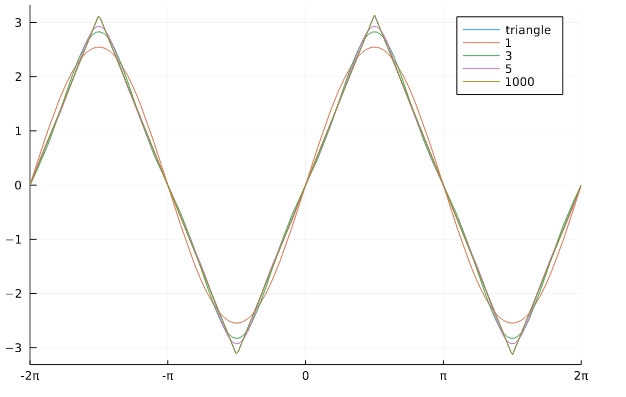
この例では、フーリエ級数は元の関数に一様収束しています。すなわち、関数とフーリエ級数の差の上限（最大値のようなもの）が0に近づいていくのです。

\(f\)が\(C^1\)級（1回連続微分可能）で、周期性\(f(-L)=f(L)\)を持ち、導関数が二乗可積分\(f^{\prime}\in L^2\)とする。

このとき、フーリエ級数は元の関数に一様収束する。

\[ \begin{aligned}\lim_{N\to \infty}\|f-S_N(x)\|_{C^0}=0\end{aligned} \]

\[ \begin{aligned}\|f-S_N(x)\|_{C^{0}} := \sup_{x \in [-L,L]}|f-S_N(x)|\end{aligned} \]

特に、各点で\(\lim_{N\to \infty} S_N(x) =f(x)\)が成り立つ（各点収束）。

\(f\)の連続性を、次のように弱めても、似た主張が成り立ちます。

\(f\)はほとんど至る所で微分可能。
\(f\)は区分的に\(C^1\)級（\([-L,L]\)において、有限個の点を除いて\(C^1\)級で、0次・1次導関数の不連続点における左極限・右極限が存在する）

上のいずれかを満たすならば、フーリエ級数は各点収束する。

連続点では、フーリエ級数と元の関数は一致する。

不連続点\(x=a\)での値は

\[ \begin{aligned}\lim_{N\to \infty}S_N (a) = \\ \frac{\lim_{x\nearrow a} f(x)+\lim_{x\searrow a} f(x)}{2}\end{aligned} \]

となります（ディリクレの展開定理）。

参考：黒田「関数解析」、杉浦「解析演習」

三角波の例ならば、\([-\pi,\pi]\)において、\(f\)には折れ曲がった点\(x= \pm \frac{\pi}{2}\)、すなわち\(f^{\prime}\)に不連続点があります。しかしそうした例外を除いては\(C^1\)級の関数で、導関数の値も有限なので、区分的に\(C^1\)級です。したがって、フーリエ級数は元の関数にすべての点で収束するわけです。

\(f\)の仮定をより強めて、\(f\)が（例外なしに）\(C^1\)級であるときは、フーリエ級数は一様収束し、項別微分可能となります。これは熱方程式を解くために応用されるものです。

参考：関数項級数の一様収束、Mテストとは：熱方程式への応用

以上、フーリエ級数の収束条件について、L^2収束、一様収束、不連続点での値に関する結果を紹介してきました。

収束に関する話は難しいですが、まずはこの記事でイメージを掴んでもらえたら嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。