どうも、木村(@kimu3_slime)です。
今回は、三角波とは何か、そのフーリエ級数展開の求め方を紹介します。
三角波とは
三角波(triangle wave)とは、次の図のように、三角形の形が繰り返す波のことです。三角関数のなす波とは別物なので注意。
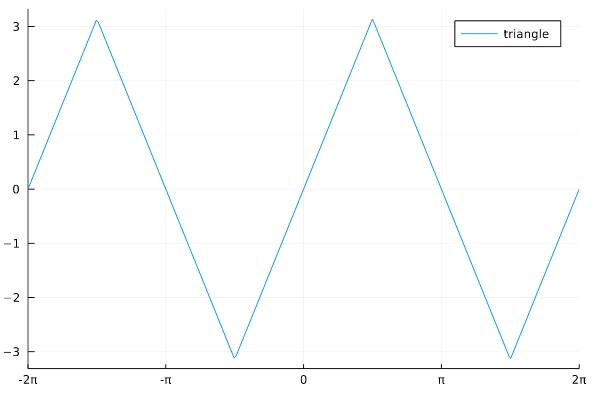
数学的には
\[ \begin{aligned}f(x)= \begin{cases}2x & (0 <x <\frac{\pi}{2} )\\-2(x-\pi) & (\frac{\pi}{2}<x <\pi)\end{cases}\end{aligned} \]
という関数を、奇関数として(\(f(x)=-f(x)\)を満たすように)、周期\(2\pi\)で周期的に拡張した(\(f(x)= f(x+2n\pi)\))ものです。
一本の関数として表すならば、
\[ \begin{aligned}f(x)= 4\pi | \frac{x+\frac{\pi}{2}}{2\pi} – \lfloor \frac{x+\frac{\pi}{2}}{2\pi}\rfloor| – \pi\end{aligned} \]
です。ここで、\(\lfloor x\rfloor\)は床関数(\(x\)以下の最大の整数)を表しています。おおざっぱに言えば、のこぎり波を絶対値を取ることで三角波に変えています。その後、シフト(平行移動)や係数の調整を行ったものです。
音として三角波を聞いてみると、サイン波に近くノイズの少ない音と感じられます。
フーリエ級数展開の求め方
では、三角波のフーリエ級数展開を求めてみましょう。
今回は奇関数となるように設定したので、奇関数のフーリエ級数展開、係数は次のよう単純化されます。
\[ \begin{aligned}f(x)=\sum_{n=1}^\infty b_n \sin nx\end{aligned} \]
\[ \begin{aligned}b_n = \frac{2}{\pi}\int_0^\pi f(x) \sin nx dx\end{aligned} \]
これを計算してみましょう。途中でたくさんのキャンセルが起こります。
\[ \begin{aligned} &b_n\\ &= \frac{2}{\pi}(\int_0^\frac{\pi}{2} 2x \sin nx dx+\int_\frac{\pi}{2}^\pi (-2(x-\pi) ) \sin nx dx) \\ &= \frac{2}{\pi}([-\frac{2}{n} x \cos nx]_0^\frac{\pi}{2} +\frac{2}{n} \int_0^\frac{\pi}{2} \cos nx dx \\ &+ [\frac{2}{n} x\cos nx]_{\frac{\pi}{2}}^{\pi}-\frac{2}{n} \int_\frac{\pi}{2}^\pi \cos nx dx \\ & -\frac{2\pi}{n}[\cos nx]_{\frac{\pi}{2}}^{\pi})\\ &=\frac{2}{\pi}(\frac{2}{n^2} [\sin nx]_0 ^\frac{\pi}{2} -\frac{2}{n^2} [\sin nx]_\frac{\pi}{2}^{\pi}) \\ &= \frac{8}{n^2\pi} \sin \frac{n\pi}{2} \\ &= \begin{cases}\frac{8}{n^2\pi} & (nが奇数かつ4で割ったあまりが1)\\ -\frac{8}{n^2\pi} & (nが奇数かつ4で割ったあまりが3)\\0 & (nが偶数)\end{cases}\end{aligned} \]
となりました。
フーリエ係数、各周波数に対する\(\sin nx\)の強さ・振幅、すなわちスペクトルは次の通りです。
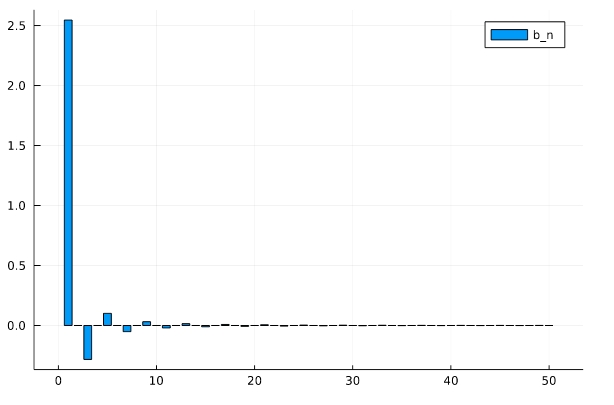
係数は\(1/n^2\)のペースで急激に小さくなっていきます。\(b_1\)、すなわち\(\sin x\)の成分が強く含まれていることがわかりますね。
三角波のフーリエ級数展開は、次のようになりました。
\[ \begin{aligned}f(x)=\sum_{n=1}^\infty \frac{8}{n^2\pi} \sin \frac{n\pi}{2} \sin nx\\ = \frac{8}{\pi}\sin x -\frac{8}{9\pi}\sin 3x +\frac{8}{25 \pi} \sin 5x – \cdots\end{aligned} \]
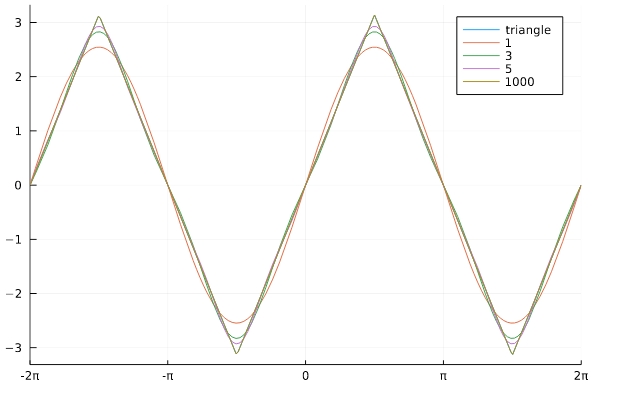
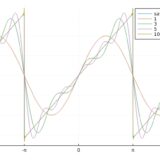
\( \frac{8}{\pi}\sin x\)の時点で、元の三角波にそこそこ近い形になっています。三角波の見た目がサイン波に近い関数ということが、フーリエ係数の計算からもわかりましたね。
以上、三角波とは何か、そのフーリエ級数展開の求め方を紹介してきました。
矩形波、のこぎり波と合わせて、簡単な波の例としてフーリエ級数展開を計算してみると良いと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
Partial Differential Equations (Graduate Studies in Mathematics)
Amer Mathematical Society (2010-04-02T00:00:01Z)
¥9,531 (中古品)
こちらもおすすめ
矩形波とは:フーリエ級数展開の求め方、ギブス現象、ライプニッツの級数