どうも、木村(@kimu3_slime)です。
今回は、複素ポテンシャルとは何か、円環領域を例に紹介します。
複素ポテンシャルは、実ポテンシャルの問題を複素の問題に持ち込むために利用されるものです。
実ポテンシャル関数\(\Phi\)とは、ラプラス方程式
\[ \begin{aligned}\Delta \Phi =\frac{\partial^2 \Phi }{\partial x^2}+\frac{\partial^2 \Phi }{\partial y^2}=0\end{aligned} \]
を満たす関数のことです。調和関数とも。電気、熱、流体のような物理に得られるポテンシャルは、ラプラス方程式を満たすことが知られています。
調和関数\(\Phi\)に対しては、コーシー・リーマンの方程式を使って、その共役調和関数\(\Psi\)が(実定数の差を除いて)定まります。そこで、それらを合わせてできる正則関数
\[ \begin{aligned}F(z):=\Phi +i \Psi\end{aligned} \]
を、複素ポテンシャル(complex potential)と呼びます。
複素ポテンシャルを考えると、2次元の実ポテンシャル\(\Phi\)を調べるために、複素解析の理論が使えます。正則関数は\(f^{\prime}(z)\neq 0\)となる点では等角写像(角度を保存)で、\(\Phi = C_1\)という等高線と\(\Psi = C_2\)という等高線は常に直交することが知られています。
物理的には、ポテンシャルと力は直交するので、\(\Psi\)の等高線は力線(lines of force)と呼ばれます。例えば\(\Phi\)が電気ポテンシャルを表すとき、\(\Psi\)の等高線は電気力線となるわけです。
また、\(Phi\)が流体における速度ポテンシャルであるとき、\(F\)は複素速度ポテンシャル、\(\Psi\)は流れ関数と呼ばれています。
より具体的に考えましょう。以下の図のような円環領域において、ポテンシャル\(\Phi\)を求めます。

この領域においてラプラス方程式を解くと、\(\Phi = a\log r +b\)となることが知られています。
その共役調和関数\(\Psi\)を求めましょう。対数関数の主値\(\mathrm{Log\,} z := \log |z| + i\mathrm{Arg}z\)が正則となることを見越して、\(\Psi = a\mathrm{Arg}z = a\mathrm{arctan}\frac{y}{x}\)とします(偏角の主値)。コーシー・リーマンの方程式
\[ \begin{aligned}\Phi _x = \Psi _y\end{aligned} \]
\[ \begin{aligned}\Phi _y = -\Psi _x\end{aligned} \]
を満たすことを示せば良いです。合成関数の微分、逆三角関数の微分などを使って微分を計算すると、
\[ \begin{aligned}\Phi_x =a \frac{1}{\sqrt{x^2+y^2}}\frac{1}{2} 2x \frac{1}{x^2+y^2}\\ =a \frac{x}{r}\end{aligned} \]
\[ \begin{aligned}\Psi _y = a \frac{1}{x} \frac{1}{1+(\frac{y}{x})^2}\\ =a \frac{x}{r}\end{aligned} \]
\[ \begin{aligned}\Phi_y =a \frac{y}{r}\end{aligned} \]
\[ \begin{aligned}\Psi _x = -a \frac{y}{x^2} \frac{1}{1+(\frac{y}{x})^2}\\ =-a \frac{y}{r}\end{aligned} \]
となるので、\(\Psi\)が共役調和関数となることがわかりました。
よって、複素ポテンシャルは
\[ \begin{aligned}F(z)=a \log r + b + i a\mathrm{Arg}z \\ = a\mathrm{\,Log} z +b\end{aligned} \]
となります。実対数関数によるポテンシャルの複素ポテンシャルが、複素対数関数の主値となっているわけです。
力線を図示してみましょう。\(\Psi = a\mathrm{Arg}z = C\)とは、偏角が一定である曲線、つまり原点を中心とした放射直線となります。
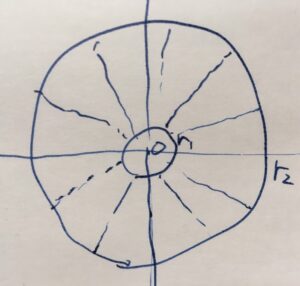
これは物理的には、原点からの湧き出しまたは吸い込みと解釈できます。
\(\Phi\)の等高線は同心円なので、\(\Psi\)の等高線(放射直線)と直交していることも確かにわかりますね。
以上、複素ポテンシャルとは何か、円環領域を例に紹介してきました。
平面的なポテンシャルの分析が、調和関数を介して複素関数の理論に持ち込むことができます。その簡単なケースとして、円環領域における複素ポテンシャルを知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Kreyszig, E: Advanced Engineering Mathematics
Wiley John + Sons (2011-05-03T00:00:01Z)
¥10,314 (中古品)
岩波書店 (2003-12-12T00:00:01Z)
¥2,640
日本評論社 (2009-06-01T00:00:01Z)
¥5,170
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740
こちらもおすすめ
同軸円筒領域におけるポテンシャル:2次元ラプラス方程式の解き方