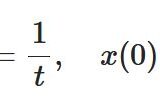どうも、木村(@kimu3_slime)です。
今回は、空気抵抗があるときの落下運動、終端速度とは何か、運動方程式を解きながら紹介します。
空気抵抗があるときの落下運動
空気抵抗がないときの落下運動は、高校物理で扱う基本的なものです。ボールを投げると放物線を描く、というやつですね。
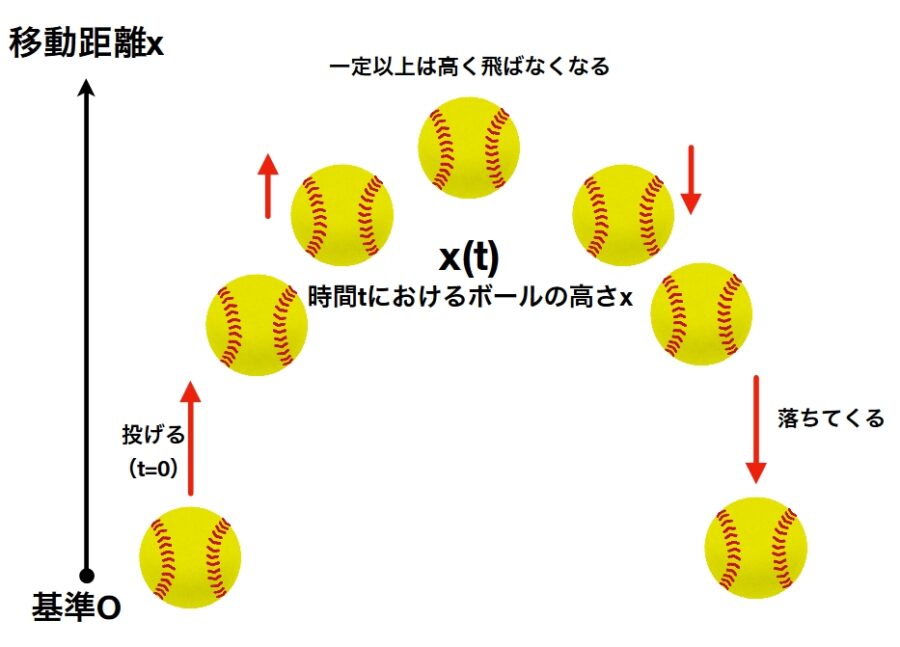
物体の位置を時間の関数\(x(t)\)、その2階微分=加速度を\(a\)として、運動方程式は
\[ \begin{aligned}ma = mg\end{aligned} \]
と表されます。\(m\)は物体の質量、\(g\)は重力加速度と呼ばれる定数です。
この運動方程式を解くと、\(v(t)= gt +v_0\)、\(x(t)= \frac{1}{2}gt^2+v_0t +x_0\)という解が得られます。これが放物運動ですね。
おおよそ落下運動とは加速していくものですが、よく考えると変な気もしてきます。
例えば雨・雨粒の落下を考えてみましょう。長い距離を時間をかけて落下しているはずですが、雨粒はそれほど速くは落下していないように見えます。実際、秒速6~8mくらいで落ち着くようです。
もしさきほどの落下運動の式が正しいなら、\(v(t)= gt +v_0\)と時間が経つにつれいくらでも速度は大きくなるはずですが、現実には速度には上限がありそうです。
そこで、空気抵抗(air resistance)というものを考えます。落下が速くなるほど、物体と空気との摩擦によって逆向きの力が働くと。
ここでは、\(F= -kv\)と速度に比例するような抵抗を考えます。\(k\)は抵抗の強さを表す定数(空気抵抗係数)です。すると、空気抵抗があるときの落下運動の運動方程式は
\[ \begin{aligned}ma =mg -kv\end{aligned} \]
となります。
\(k\)が十分小さくて、重力に対して無視できるような場合は、単に\(ma=mg\)という式になります。つまり、抵抗のない式は抵抗のある式の近似式と言えますね。
運動方程式を微分方程式として解いてみましょう。これは変数分離型と呼ばれる形で、簡単に解くことができます。
\[ \begin{aligned} m \frac{dv}{dt} =mg -kv\end{aligned} \]
を右辺で割ると、
\[ \begin{aligned}\frac{m}{mg-kv} \frac{dv}{dt} =1\end{aligned} \]
です。ここで両辺を\(t\)について積分すれば、
\[ \begin{aligned}\int \frac{m}{mg-kv} dv = \int 1 dt\end{aligned} \]
なので、
\[ \begin{aligned}-\frac{m}{k}\log (mg-kv) = t+C\end{aligned} \]
となり、整理して両辺の指数関数を取れば
\[ \begin{aligned}mg -kv = Ce^{-\frac{k}{m}t}\end{aligned} \]
となります(\(C\)は積分定数で、適宜置き直している)。これを\(v\)について整理すれば、
\[ \begin{aligned}v = \frac{1}{k}(mg- Ce^{-\frac{k}{m}t})\end{aligned} \]
となり、初速度を\(v(0)= v_0\)とすると、
\[ \begin{aligned}v(t)=\frac{1}{k}(mg- (mg-kv_0)e^{-\frac{k}{m}t})\end{aligned} \]
となりました。これが運動方程式の解です。
特に、自由落下\(v_0 = 0\)のときは
\[ \begin{aligned}v(t)=\frac{mg}{k}(1-e^{-\frac{k}{m}t})\end{aligned} \]
となります。

最初はグッと加速しますが、指数関数の効果によって、すぐに一定の速度に落ち着くことがわかります(\(\lim_{t \to \infty}e^{-\frac{k}{m}t}=0\))。
\[ \begin{aligned}v_{\infty}:=\lim _{t \to \infty}v(t)=\frac{mg}{k}\end{aligned} \]
を終端速度(terminal velocity)と呼びます。
終端速度は、運動方程式において力の釣り合いが取れた式、\(mg-kv=0\)より\(v= \frac{mg}{k}\)とも言えます。(こう議論できるのは、\(v_\infty\)が方程式の安定な平衡解であるからです)
空気抵抗を考えた運動方程式では、物体が際限なしに加速することはなく、終端速度という限界があることがわかりました。
物体の位置も求めてみましょう。速度の式を積分すると、
\[ \begin{aligned}x(t)=\frac{1}{k}(mgt+\frac{m(mg-kv_0)}{k}e^{-\frac{k}{m}t}) \\+x_0-\frac{m(mg-kv_0)}{k^2}\end{aligned} \]
となります。自由落下\(v_0=x_0=0\)のときは、
\[ \begin{aligned}x(t)= \frac{mg}{k}t +\frac{m^2g}{k^2}(e^{-\frac{k}{m}t}-1)\end{aligned} \]
です。

空気抵抗を考えると、落下運動はすぐにほぼ等速直線運動(その速度は終端速度)になる、というわけですね。
以上、空気抵抗があるときの落下運動、終端速度とは何か、運動方程式を解いて紹介してきました。
今回は簡単のため\(F=-kv\)という1次の抵抗(粘性抵抗)を考えました。それは速度が遅いときに有効ですが、より速度が速いときは2次の抵抗\(F=-kv^2\)(慣性抵抗)が支配的になります。
2次のケースは少し計算が複雑になりますが、どちらのケースを考えても、(有限の)終端速度が存在するということは変わりません。
1次の抵抗の計算は難しくないので、ぜひ実際に計算して、終端速度というものが導けることに納得してみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)