どうも、木村(@kimu3_slime)です。
今回は、ロジスティック方程式の解き方として、ベルヌーイの方程式というものを紹介します。
ロジスティック方程式の解き方
ロジスティック方程式とは、
\[ \begin{aligned}\frac{du}{dt}= ru – \frac{r}{K}u^2\end{aligned} \]
と表される微分方程式でした。ここで\(r,K>0\)は定数です。この方程式は生物の個体数\(u(t)\)の変化を説明するものです。
この方程式は、変数分離形として、そのまま積分して解くことができます。
今回は、ロジスティック方程式を一般化した方程式
\[ \begin{aligned}\frac{dx}{dt}+P(t)x=Q(t)x^a\end{aligned} \]
を考えることにします。ここで\(a\)は実数です。これをベルヌーイの方程式(Bernoulli’s equation)、ベルヌーイ形の方程式と呼びます。
\(a=0,1\)のときは1階線形微分方程式ですね。\(a=2\)、\(P(t)=-r\)、\(Q(t)=-\frac{r}{K}\)のときが、ロジスティック方程式です。
ロジスティック方程式、ベルヌーイの方程式は一般的には、1階線形微分方程式ではありません(非線形方程式)。しかし、変数変換によって、線形微分方程式に帰着させることができます。それを紹介しましょう。
まずはロジスティック方程式の解き方を紹介します。
\(v = u^{1-a}=\frac{1}{u}\)という変数変換を考えてみましょう。合成関数の微分を使って計算すると、
\[ \begin{aligned} \frac{dv}{dt}&= -\frac{1}{u^2}\frac{du}{dt} \\&= -\frac{1}{u^2}(ru – \frac{r}{K}u^2)\\ &= -rv +\frac{r}{K}\end{aligned} \]
と、\(v\)について線形な方程式に変換することができました。厄介なべき乗\(x^2\)の部分がうまくキャンセルされていますね。
ここからは、線形微分方程式の解き方を使っていきます。まず、同次形の方程式
\[ \begin{aligned}\frac{dv}{dt}= -rv\end{aligned} \]
を解きます。これは変数分離形なので、積分によって解けて、\(v(t)=Ce^{-rt}\)です。
定数変化法として、\(v(t)= C(t)e^{-rt}\)を元の方程式に代入しましょう。
\[ \begin{aligned}\frac{dC}{dt}e^{-rt}-rCe^{-rt}= -rCe^{-rt}+\frac{r}{K}\end{aligned} \]
\[ \begin{aligned}\frac{dC}{dt}= \frac{r}{K}e^{rt}\end{aligned} \]
となります。これは積分によって解けて、
\[ \begin{aligned}C(t)= \frac{1}{K}e^{rt} +C\end{aligned} \]
となりました。元の方程式に戻し、変数変換も戻すと
\[ \begin{aligned} u(t) &= \frac{1}{v(t)}\\&= \frac{1}{C(t)e^{-rt}}\\&= \frac{K}{1+KCe^{-rt}} \end{aligned} \]
となります。初期条件を\(u(0)=u_0, u_0 \neq 0\)とすれば、
\[ \begin{aligned}u(t)= \frac{K}{1+ (\frac{K}{u_0}-1) e^{-rt}}\end{aligned} \]
となります。\(u_0=0\)のときは、\(u(t)=0\)は確かに方程式を満たすので、それも解と言えます。
よって、ロジスティック方程式の解が求められました。
この関数は\(0 < u_0 < K\)のとき、\(t\)について単調増加です。また、指数関数の効果から\(\lim_{t \to -\infty}u(t)= 0\)、\(\lim_{t\to \infty}u(t)= K\)です。したがって、
\[ \begin{aligned} 0 < u(t) <K\end{aligned} \]
と、\(0,K\)の間を変動するグラフとなります。
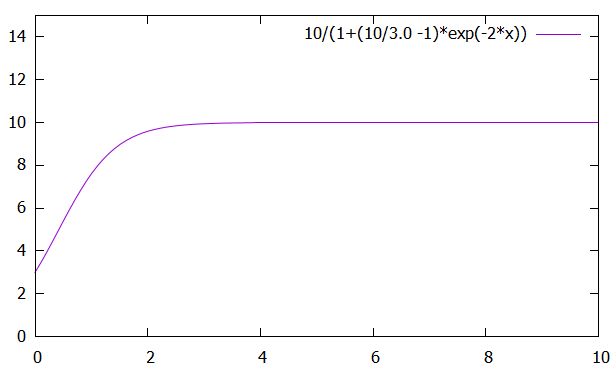
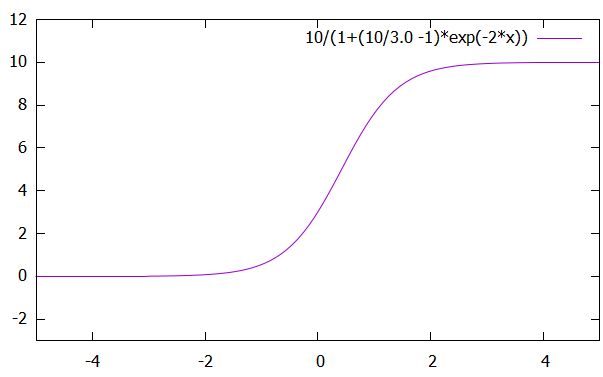
この方程式の解が描くS字の曲線は、ロジスティック曲線、シグモイド関数と呼ばれています。
ベルヌーイの方程式の解き方
ベルヌーイの方程式
\[ \begin{aligned}\frac{dx}{dt}+P(t)x=Q(t)x^a\end{aligned} \]
も、ロジスティック方程式と同じように解くことができます。
\(y= x^{1-a}\)という変数変換を考えましょう。すると、
\[ \begin{aligned} \frac{dy}{dt}&= (1-a)x^{-a}\frac{dx}{dt} \\&= (1-a)x^{-a}(-P(t)x – Q(t)x^a)\\ &= (a-1)(P(t) y+Q(t))\end{aligned} \]
と\(y\)に関する線形方程式になりました。後は、線形方程式の解き方を適用するだけです。
変数変換の見つけ方としては、\(y=x^{b}\)と一般的に置いてみると良いでしょう。
\[ \begin{aligned} \frac{dy}{dt}&= bx^{b-1}\frac{dx}{dt} \\&= bx^{b-1}(-P(t)x – Q(t)x^a)\\ &= -b(P(t) y+Q(t)x^{b-1+a})\end{aligned} \]
となるので、\(b-1+a=0\)とべきが消えるような選び方をすれば良いですね。
以上、ロジスティック方程式の解き方、ベルヌーイの方程式についても紹介してきました。
時間に依存しないロジスティック方程式は、変数分離形としても解くことができます。ですが、ベルヌーイの方程式として解く、非線形方程式を変数変換によって線形方程式に帰着させる、という解き方も面白いと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)