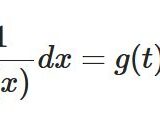どうも、木村(@kimu3_slime)です。
今回は、1階線形微分方程式の解き方と証明、積分因子、定数変化法について紹介します。
前提知識:常微分方程式の変数分離形とは:証明と注意点(特異解)
1階線形微分方程式とは
今回考えるのは、
\[ \begin{aligned}\frac{dx}{dt}(t)+P(t)x(t) =Q(t) \end{aligned} \]
と表される微分方程式です。これを1階線形微分方程式(first order linear differential equation)と呼びます。1階とは、1回微分\(\frac{dx}{dt}\)が登場する微分方程式、という意味です。
例えば、
\[ \begin{aligned}\frac{dx}{dt}=x\end{aligned} \]
\[ \begin{aligned}\frac{dx}{dt}=-x\end{aligned} \]
は線形微分方程式です。\(P(t)\)が\(1\)や\(-1\)で、\(Q(t)=0\)です。
特に、\(Q(t)=0\)となっている方程式を、同次方程式(homogeneous equation)、斉次方程式と呼びます。そうでない方程式を、非同次方程式(nonhomogeneous equation)と呼びます。
参考:人類は必ず食糧問題に直面する? マルサスの法則と微分方程式、ニュートンの冷却法則とは:意味と解き方、空気抵抗があるときの落下運動、終端速度とは:運動方程式を解く
また、
\[ \begin{aligned}\frac{dx}{dt}=x-x^2\end{aligned} \]
は線形微分方程式ではありません。
方程式が線形であるとは、方程式の解の和、スカラー倍がまた解となることです。
\(Q(t)=0\)のとき、\(x_1,x_2\)を方程式の解、\(c\)をスカラーとすると、
\[ \begin{aligned} & \frac{d}{dt}(cx_1+x_2)+P(t)(cx_1+x_2) \\&=c\frac{dx_1}{dt}+\frac{dx_2}{dt} +P(t)cx_1 +P(t)x_2 \\ &= c(\frac{dx_1}{dt}+P(t)x_1)+(\frac{dx_2}{dt} +P(t)x_2 )\\ &= 0\end{aligned} \]
となるので、同次のときは線形方程式であることがわかりました。
非同次のときは線形方程式になるとは限らないのですが、同次のケースを考えれば線形方程式となっているとき、非同次の方程式も線形と呼ぶ慣習があるようです。
参考:数学・科学における「線形・非線形」の違いを詳しく解説、波の重ね合わせの原理はなぜ成り立つ? 波動方程式入門、線形写像かどうか調べる方法をわかりやすく解説
積分因子を使った解法
同次方程式のとき
\[ \begin{aligned}\frac{dx}{dt}(t)+P(t)x(t) =0 \end{aligned} \]
は、変数分離形なので、積分によって解くことができます。
なので、一般的な(非同次の)線形微分方程式の解き方を考えていきましょう。
具体例として、\(P(t)=1\)、\(Q(t)=\sin t\)、
\[ \begin{aligned}\frac{dx}{dt}+x(t)=\sin t\end{aligned} \]
という方程式を考えます。ニュートンの冷却法則で考えれば、冷却は起こるものの、外気温が\(\sin t\)によって周期的に変化している、という状況です。
微分方程式を解くことは、\(x(t)=\)という形の式を得たいわけで、そのために積分を使えないか考えます。そこでまず紹介するのが、積分因子という考え方です。
\(I(t)\)という関数で、積分をするのに都合が良いものを見つけられないでしょうか。すなわち、もし方程式を
\[ \begin{aligned}\frac{d}{dt}(xI)= I \sin t\end{aligned} \]
という形に持っていけたら、\(t\)について積分して、方程式を解くことができますね。
これは実際に可能です。積の微分を使って展開すると、
\[ \begin{aligned}\frac{d}{dt}(xI)= \frac{dx}{dt}I+x \frac{dI}{dt}\end{aligned} \]
となるので、その右辺を方程式の左辺の\(I\)倍と一致させるためには、
\[ \begin{aligned}\frac{dI}{dt}= I\end{aligned} \]
であれば良いです。これは簡単に解くことができて、\(I(t)= e^t\)となります。(\(I(t)=e^t+C\)という候補があるが、積分定数を\(C=0\)と選んで式を簡単にした。)
このように定めれば、
\[ \begin{aligned}\frac{d}{dt}(xI)= I \sin t\end{aligned} \]
が得られるので、両辺を\(t\)について積分すれば
\[ \begin{aligned}xe^t = \int e^t \sin t dt\end{aligned} \]
となります。
右辺は部分積分によって、次のように計算できます(高校数学)。
\[ \begin{aligned} \int e^t \sin t dt &=e^t \sin t -\int e^t \cos t dt +C \\&= e^t \sin t -e^t \cos t dt\\ & -\int e^t \sin t dt +C \end{aligned} \]
これを求める積分について整理すれば、
\[ \begin{aligned}\int e^t \sin t dt = \frac{1}{2}e^t (\sin t – \cos t)\end{aligned} \]
が得られます。右辺をさらに三角関数の加法定理によってまとめると、
\[ \begin{aligned} &\frac{1}{2}(\sin t -\cos t)\\ &=\frac{1}{\sqrt{2}}(\sin t \frac{1}{\sqrt{2}} +\cos t (-\frac{1}{\sqrt{2}})) \\ &=\frac{1}{\sqrt{2}} (\sin t \cos (-\frac{\pi}{4}) +\cos t \sin (-\frac{\pi}{4}))\\ &=\frac{1}{\sqrt{2}} \sin (t-\frac{\pi}{4}) \end{aligned} \]
となります。これらの結果をまとめれば、
\[ \begin{aligned} x(t)&= e^{-t}(e^t \frac{1}{\sqrt{2}} \sin (t-\frac{\pi}{4}) +C)\\ &= \frac{1}{\sqrt{2}} \sin (t-\frac{\pi}{4}) +Ce^{-t}\end{aligned} \]
で、初期条件を\(x(0)=x_0\)とすれば
\[ \begin{aligned}x(t)= \frac{1}{\sqrt{2}} \sin (t-\frac{\pi}{4}) +(x_0+\frac{1}{2})e^{-t}\end{aligned} \]
と解が求められました。
\(t\to \infty\)としたときに、\(e^{-t}\)の項は減衰によって影響がなくなり、ほとんど\(\sin t\)の状態に落ち着いていくことがわかりますね。


さまざまな初期条件の解が極限で周期解に近づいていくとき、その周期解は極限周期軌道(リミットサイクル)と呼ばれています。どんな初期条件から始めても、取りうる値は\(\frac{1}{\sqrt{2}} \sin (t-\frac{\pi}{4})\)に近づいていきますね。
参考:極限集合の性質を明らかにするポアンカレ・ベンディクソンの定理
今までの方法は、一般的に議論できます。
\[ \begin{aligned}\frac{dx}{dt}(t)+P(t)x(t) =Q(t) \end{aligned} \]
という方程式に対し、
\[ \begin{aligned}\frac{dI}{dt}= P(t)I(t)\end{aligned} \]
を満たすような関数\(I\)を見つけましょう。これは変数分離形なので積分計算によって求められて、
\[ \begin{aligned}I(t):= e^{\int P(t)dt}\end{aligned} \]
とすれば良いです。この関数を積分因子(integrating factor)と呼びます。
積分因子を方程式の両辺にかけると
\[ \begin{aligned}\frac{dx}{dt}(t)I(t)+P(t)I(t)x(t) =I(t)Q(t) \end{aligned} \]
となるので、積の微分を使ってまとめれば
\[ \begin{aligned}\frac{d}{dt}(xI) = IQ\end{aligned} \]
で、積分ができるようになりました。積分できるようにするための因子なので、積分因子です。両辺を\(t\)について積分して整理すれば、
\[ \begin{aligned} x(t) = e^{-\int P(t)dt}(\int e^{\int P(t)dt}Q(t)dt+C)\end{aligned} \]
と解が得られます。(文字\(t\)が重複していますが、ひとつの積分ごとに区別するよう気をつけましょう。)
この解の表示式は、公式として覚えるよりは、積分因子による導き方を覚えて導出したほうが良いと思います。
定数変化法による解法
以上の解法は、定数変化法という別の見方によって導くこともできます。
まず、同次方程式
\[ \begin{aligned}\frac{dx}{dt}(t)+P(t)x(t) =0 \end{aligned} \]
は変数分離形なので解けて、解としては
\[ \begin{aligned}x(t)=Ce^{-\int P(t)dt}\end{aligned} \]
が得られます。ここで新たに、\(C\)を\(t\)の関数\(C(t)\)と仮定して、この解\(x_1(t)=C(t)e^{-\int P(t)dt}\)を非同次の方程式に代入してみましょう。
積の微分と、微積分学の基本定理より(\(e^{-\int P(t)dt}=-P(t)e^{-\int P(t)dt}\))に注意して計算すれば、
\[ \begin{aligned} &\frac{dx_1}{dt}(t)+P(t)x_1(t) \\&=\frac{dC}{dt}e^{-\int P(t)dt} +CPe^{-\int P(t)dt} +PCe^{-\int P(t)dt} \\&= \frac{dC}{dt}e^{-\int P(t)dt} \\&= Q(t)\end{aligned} \]
となります。これを\(C(t)\)に関する微分方程式として見れば、積分することで
\[ \begin{aligned}C(t) = \int e^{\int P(t)dt} Q(t)dt+C\end{aligned} \]
と求められました(この積分は、積分因子のときにも見ましたね)。よって、
\[ \begin{aligned} x(t)&= C(t)e^{-\int P(t)dt} \\&= e^{-\int P(t)dt}( \int e^{\int P(t)dt} Q(t)dt+C)\end{aligned} \]
が非同次の方程式の一般解として求められました。
同次方程式の解
\[ \begin{aligned}x(t)=Ce^{-\int P(t)dt}\end{aligned} \]
の定数\(C\)を、変数(関数)\(C(t)\)として非同次の方程式に代入し、それを満たすような関数を見つける。この方法は、定数変化法(variation of constants)、係数変化法(variation of parameters)と呼ばれます。
手順としては、定数変化法は覚えやすいですね。同次形の方程式を解き、そこで出てくる定数を変数(関数)と仮定して、非同次方程式に当てはめて解くことで、非同次の方程式を解くことができます。
以上、1階線形微分方程式の解き方と証明:積分因子、定数変化法について紹介してきました。
積分因子の方法は、要は積の微分を使える形にして積分するということです。定数変化法は、同次方程式から解いて非同次方程式の解が得られる方法です。
どちらも、1階線形微分方程式に限らず使える微分方程式の基本的な解き方なので、導出や証明を含めて理解してみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
空気抵抗があるときの落下運動、終端速度とは:運動方程式を解く
極限集合の性質を明らかにするポアンカレ・ベンディクソンの定理