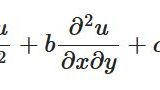1次元のラプラス方程式の解き方

どうも、木村（@kimu3_slime）です。

今回は、1次元のラプラス方程式の解き方を紹介します。

1次元のラプラス方程式は、

\[ \begin{aligned}\frac{d^2u}{dx^2}=0\end{aligned} \]

と表される方程式です。2次元以上だと空間2回偏微分の和が0になるという条件ですが、1次元では単に常微分方程式の問題となっています。

この問題は、例えば熱方程式の定常問題（時間変化しなくなった解）として現れます。

この方程式は簡単に解くことができます。単に\(x\)について2回積分すれば良いのです。

\[ \begin{aligned}\frac{du}{dx}= C_1\end{aligned} \]

\[ \begin{aligned}u(x)= C_1x +C_2\end{aligned} \]

区間を\([0,1]\)として、境界条件を\(u(0)=1\)、\(\frac{du}{dx}(1)=0\)とすると、解は\(u(x)=1\)となります。この境界条件は、\(x=0\)で一定の温度、\(x=1\)で断熱条件に対応したものです（混合境界条件）。

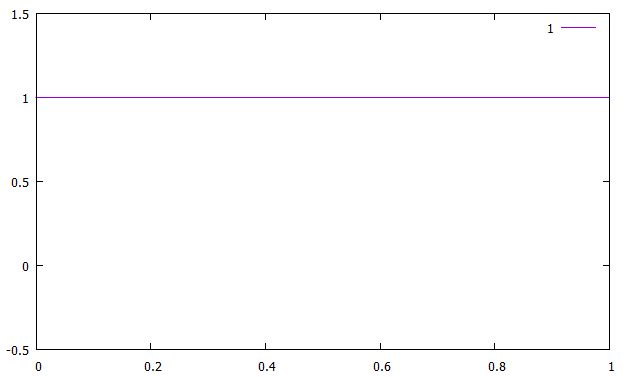
ディリクレ境界条件\(x(0)=x(1)=0\)のときの熱方程式の解は、次のようになります。

これに対応するラプラス方程式の解は、\(u(x)=0\)です。一定の温度に収束するのが見て取れますね。

以上、1次元のラプラス方程式の解き方を紹介してきました。

2次元以上のラプラス方程式を解くならばフーリエ級数が必要になりますが、1次元ならば非常に簡単で、解は1次関数となります。

ラプラス方程式のイメージがつかみにくいと感じたならば、まずは1次元のケースを考えてみてはいかがでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。

posted with AmaQuick at 2021.08.22

Edwards, C. Henry(著), Penney, David E.(著), Calvis, David T.(著)
Pearson (2016-03-02T00:00:00.000Z)

￥4,910

posted with AmaQuick at 2021.08.27

Kreyszig, Erwin(著)
John Wiley & Sons Inc (2011-05-03T00:00:01Z)

￥6,333 (中古品)

posted with AmaQuick at 2021.08.22

英二, 柳田(著), 伸一郎, 栄(著)
朝倉書店 (2002-01-01T00:00:01Z)

￥2,215 (中古品)

posted with AmaQuick at 2021.10.08

Evans, Lawrence C.(著)
Amer Mathematical Society (2010-04-02T00:00:01Z)

￥9,531 (中古品)

こちらもおすすめ