線形代数学(linear algebra)は、微積分学と並び、大学で数学をする人はもちろん、自然科学や工学、社会科学や人文科学を学ぶすべての人が身につけて損はない数学(教養数学)です。高校数学で言えば、ベクトルや行列の分野が基礎となっています。
僕個人としては、具体的な計算の難しさや、抽象的な\(n\)次行列・\(n\)次元空間が出てきて、大学1年のときに学ぶのに苦労した科目でもあります(笑)。
この記事では、線形代数学に関する記事を分野ごとにまとめて紹介します。特に重要なキーワードは
- ベクトル、行列
- 線形方程式、ランク、ガウスの消去法
- 可逆行列、逆行列、行列式
- 線形空間、線形独立、次元、線形写像
- 内積、ノルム、直交化
- 固有値・固有ベクトル、対角化
です。知らないものがあれば、優先して学ぶと良いでしょう。
目次
線形代数の使いみち、応用

線形代数は、物事を単純化(線形化)した世界の学問です。画像やウェブページのリンクといったデータは、ベクトルや行列によって離散的:デジタルに表現できます。1次関数の一般化に対応した、行列によって表される線形モデルは、科学全般で用いられる最も単純なモデルのひとつです。
線形代数学の応用:CG・画像処理(拡大縮小・反転、回転、せん断)について
なぜ線形代数を学ぶ? Googleのページランクに使われている固有値・固有ベクトルの考え方
ベクトル、行列の扱い
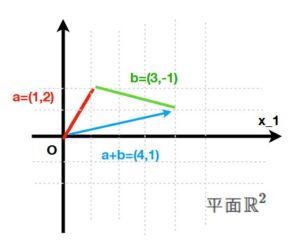
ベクトルは「数をいくつか並べたもの」として定義できますが、それは「向きと大きさを持った矢印」としても解釈できます。行列もまた「数を並べたもの」ですが、それはベクトルを別のベクトルに変える変換(関数)として、幾何学的に捉えられるものです。
線形方程式、ランク
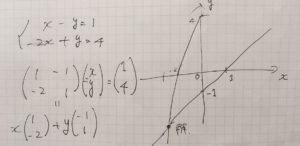
中学で学ぶ連立方程式は、つるかめ算を始めとして、物事を単純に説明するモデル:線形モデルとして利用されるものです。複雑な(連続な問題)をコンピュータで解くためにも、線形方程式に落とし込む操作が行われます(離散化)。変数は2元連立に限らず、10元、100元、一般に\(n\)元を扱えたら便利です。
線形方程式を行列で解く手順としては、行列の基本変形を使った、ガウスの消去法をぜひ身につけたいです。これは行列のランクという数値を求めるのに使えますが、他にも線形独立性の判定、逆行列の求め方など、応用が幅広いので、確実にマスターしましょう。
1次方程式を行列で解くメリット・方法・条件について、幾何学的に見る
線形方程式の解き方:ガウスの消去法と基本変形・ランク、LU分解
可逆行列(正則行列)、逆行列
線形方程式の解は、いつでもただ一つに定まるとは限りません。\(Ax =b\)の解がただひとつに求められる行列は、可逆な行列と呼ばれます。逆行列を使うと、\(x = A^{-1} b\)と解が求められます(これは線形方程式を数値的に解くという点では、効率の良くない方法ですが)。
行列式
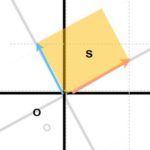
行列式は、行列が可逆かどうかを簡単に判別するできる数値です。幾何学的には、行列を変換として見たときの、面積拡大率と言えます。
なぜ行列式を学ぶのか? 固有値・固有ベクトルの求め方:固有多項式の定義
サラスの方法、n次行列式の覚え方:置換を使った定義を理解する
名前のついた行列
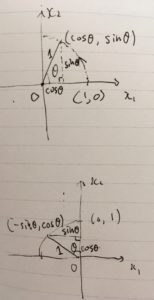
線形代数学では、名前のついた特殊な行列がたくさんあります。個別の話はめんどくさいなと思うかもしれませんが、具体的で特殊な例から馴染んでいくことで、線形代数の一般論がよりクリアに理解できるようになるでしょう。
ベクトル値関数をベクトル場として描いてみよう:ヤコビ行列と線形近似
直交ベクトルの線形独立性、正規直交基底、直交行列について解説
対称行列の性質:内積による特徴づけ、逆行列、固有値、対角化について
線形空間(ベクトル空間)、線形独立、次元
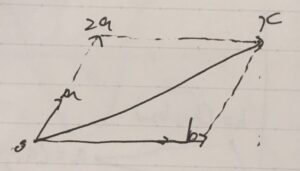
複雑なベクトルを単純なベクトルの和:線形結合として表す考え方は、線形代数の基本です。(平行でない)2本のベクトルを直線的に伸ばすと、そこに平面(直線的な空間)ができあがりますが、それが線形空間の考え方です。
線形空間、線形独立、次元の考え方は、「ベクトル」や「行列」の考え方を、より深いものにしてくれます。
実数空間、線形結合、線形部分空間、次元とは何か:2次元を例に
行列全体のなす集合が線形空間(ベクトル空間)となることの証明
連続関数、可積分関数の線形空間(関数空間)、微分と積分の線形性とは
線形写像、表現行列
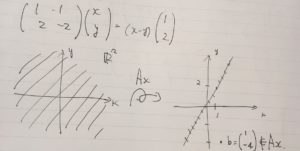
線形写像は、行列のベクトルを別のベクトルに写す側面(線形変換)を、「線形性」という面を取り出して一般化したものです。行列はさまざまな問題に現れるものですが、それを線形写像として幾何学的に調べることで、より人間にとってわかりやすい形で捉え直すことができます。
線形写像の単射・全射の条件:核・像、基底・次元との関係、証明
線形写像のランク、行列式、固有値は表現行列によらず定まることの証明
内積、ノルム
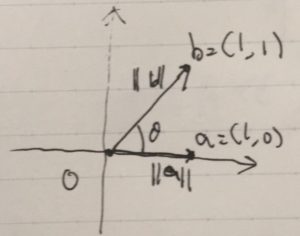
ベクトルの「大きさ」はノルム、「角度」に関連する量は内積と呼ばれ、2,3次元に限らず一般化できます。特に直交するベクトルは、基底として使いやすく重要です。関数がベクトルとして直交するという考え方をすることができ、それはフーリエ級数展開の考え方につながってきます。
線形代数の応用:関数の「空間・基底・内積」を使ったフーリエ級数展開
直交化、直和と射影
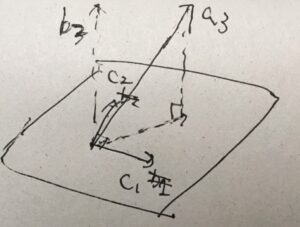
いくつかの線形独立なベクトルがあったら、それは必ず直交化することができ、その手順はグラム・シュミットの直交化法と呼ばれています。
統計学では与えられたデータに最も近い線形関係を探す最小二乗法という手法がありますが、その原理には直交射影が関わっています。
最小二乗法とは:最小二乗解の求め方、正規方程式、射影による理解
固有値、対角化、ジョルダン標準形、指数行列
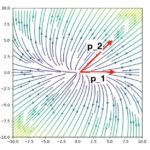

線形代数の最も大きな一つのトピックが、固有値・固有ベクトルと対角化です。僕個人としては、線形方程式や行列式の話から線形代数を学ぶのは退屈なので、固有値・対角化を大きな目標として学ぶのも良いのでは、と思っています。
行列はベクトルの変換(線形変換)として見れるわけですが、その挙動は、そのままではわかりにくいです。行列の積の計算って面倒ですよね。しかし、ある種の特殊なベクトルに対しては、\(A x = \lambda x\)と定数倍になって返ってきます。そのようなベクトルは固有ベクトル、倍率は固有値と呼ばれるものです。
固有ベクトルがうまく見つけられるときは、行列は対角行列のようにシンプルに扱えます(対角化)。たとえ対角化ができなくても、それに近い上三角行列にできます(ジョルダン標準形)。
固有ベクトルや対角化の考え方を活かすと、フィボナッチ数列のような線形漸化式が解けたり、線形常微分方程式を解くことができます。
行列の対角化可能性の定義とメリット、例、同値条件について解説
行列の相似とは:対角化との関係、不変量(ランク、行列式、固有値)
固有空間の求め方、代数的・幾何学的重複度とは:部分空間となることの証明
漸化式(フィボナッチ数列)を線形代数(線形空間、固有ベクトル)で解く方法を解説
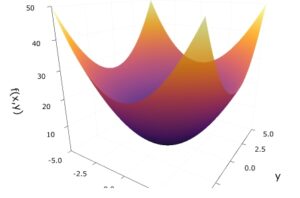
2次形式、正定値行列
2次関数の多変数への一般化として、多変数の2次関数:2次形式が考えられます。2次形式が極値を持つかどうかは微積分学において基本的な問題ですが、それは行列が正定値行列かどうかという線形代数の問題に帰着されます。
コンピュータ
線形代数の手計算は大変なので、プログラミングでも計算できるようになっておくと良いでしょう。
Julia(SymPy)でベクトルの計算をする方法(内積・ノルム・距離・角度、外積)
Julia(SymPy)で行列の和・積・転置、線形方程式を解く方法
Julia(SymPy)で行列の標準形、ランク、LU分解、線形独立性を計算する方法
Julia(SymPy)で行列の核、像、線形空間の基底と次元を求める方法
Julia(SymPy)で固有値、固有ベクトル、対角化、ジョルダン標準形を求める方法
Julia(SymPy)で行列の正定値・負定値・不定値性を判定する方法
Julia(SymPy)でQR分解、正規直交系を計算する方法
Julia(SymPy)で指数行列、線形常微分方程式を解く方法
教科書
やさしい順に並べています。
詳しくは:大学入学前に数学を予習したい人におすすめの本・勉強法
マセマ出版社 (2017-04-23T00:00:01Z)
¥1,980
マセマ出版社 (2020-02-05T00:00:01Z)
¥4,796 (コレクター商品)
サイエンス社 (2012-07-01T00:00:01Z)
¥4,356 (コレクター商品)
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社 (2015-12-22T00:00:01Z)
¥8,800
東京大学出版会 (1966-03-31T00:00:01Z)
¥1,500 (コレクター商品)