人工知能・機械学習を学ぶために必要な数学的知識とは

どうも、木村（@kimu3_slime）です。

ここ数年、ニュースなどで人工知能（AI）・機械学習といったキーワードを耳にします。

僕はそうした分野を学んだことがなかったのですが興味を持ち、「イラストで学ぶ人工知能概論」を読みました。

この本を参考に、人工知能・機械学習を学ぶ前提として必要な数学的知識を紹介します。

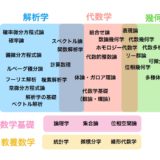
3つにまとめるなら、線形代数学、微積分学、確率論です。

人工知能・機械学習を学ぶために必要な数学的知識
こちらもおすすめ

人工知能・機械学習を学ぶために必要な数学的知識

高校数学

多くの部分で要求されるのは、大学数学というよりも、中学・高校数学のレベルです。

つまり、四則演算を知っていて、かつ記号を使った計算（初等代数学）がわかっていれば、だいたいの式を追うことはできます。

「イラストで学ぶ人工知能概論」では、機械を動かすのシステムとして、（連続システムではなく）離散システムを考えます。

そのため、機械の状態の変化は \(s_{t+1} = f(s_t,a_t)\)といった式で表されます。

時間の変数\(t\)が自然数となる値\(x_t\)を考えるので、高校数学Bで習う数列・和の記号（シグマ\(\sum\)）に慣れておいた方が良いでしょう。

線形代数学

人工知能にはさまざまな分野の知識が求められますが、多くのテーマで必要とされているのが線形代数学の知識です。

逆に、線形代数学さえ知っていれば、あとの数学は個別に必要になったときに学べばよいかと思うくらい。

例えば、迷路を解くロボットの状態や行動はベクトルを使って表現されます。

二輪で移動するロボットは、位置状態が3次元空間のベクトル\((x_t,y_t,\theta_t)\)、行動は両輪の速度からなる2次元空間のベクトル\((v^R_t,v^L_t)\)といったように。

また、ある時間\(t\)からその次の時間\(t+1\)における機械の状態遷移は、行列（線形変換）により表現されることが多いです。

例えば、

\[ \begin{aligned}P = \begin{pmatrix} p_{1,1} & p_{1,2} &p_{1,3} \\ p_{2,1} & p_{2,2} & p_{2,3} \\ p_{3,1} & p_{3,2} & p_{3,3}\end{pmatrix}= \begin{pmatrix} 0.1 & 1.0 &0.5 \\ 0.5 & 0 & 0 \\ 0.4 & 0 & 0.5\end{pmatrix}\end{aligned} \]

といった行列（状態遷移確率行列）が登場します。

線形代数学は、コンピュータの数学の言語とも言える分野なので、最初に学ぶと良いでしょう。

微積分学

機械学習やパターン認識（文字認識、画像認識、音声認識）には、微積分学の知識が必要となります。

例えば画像認識なら、多くの画像データのインプットと、分類結果などのアウトプットの対応関係を学習させます。

数学においては、対応関係は関数\(f\)として捉えられます。インプット\(x\)に対して適切なアウトプット\(f(x)\)を返せるようにしたいわけです。

多数のデータインプットをよく近似している関数を探す問題を、回帰問題（regression problem）と言います。

回帰問題を解くためには、正解のデータと関数との誤差を減らせば良いということで、最適化問題となります。

その基本的な手法である勾配法・最急降下法・最小二乗法では、偏微分の知識を使います。誤差が減るようなパラメータの方向はなんだろう……と考えれば偏微分が必要となるわけです。

機械学習より一般のシステム・機械の制御理論では、離散システムではなく連続システム（微分方程式）の理解が必要となります。

ところが、コンピュータで連続の問題を解くときも、オイラー法や有限要素法を使って離散の問題（近似）に帰着させるため、線形代数学の知識が必要となるでしょう。

確率論

僕たち人間は、間違えることがあります。機械による画像認識なども同じで、木の箱と宝箱を間違えてしまうこともあるでしょう。

現実世界に不確定要素が混じっているならば、そもそもそれを含めて行動した方が良いでしょう。過去の経験を活かして、確率的に行動すれば良いわけです。

そこで必要になってくるのが確率論です。

しかしながら、大学の数学科で確率論として習うような内容は、必ずしも必要ではないでしょう。

有限・離散の時間を扱うため、確率空間の理論は必要なく、高校の確率論程度で良いです。例えば期待値は、

\(E[A]=\sum_A f(A)P(A)\)

と表されるため、（ルベーグ）積分の知識は必ずしも必要ではありません。

確率過程やマルコフ過程の理論は知っておいた方がよりよく理解できるでしょう。

むしろ、標準的な数学の確率論の教科書では扱われていない、ベイズ理論（ベイズ確率論）の知識があったほうが良いです。

例えば、機械が前進命令を出すことを事象Bとし、実際に機械が前進したことを事象Aします。このとき、Bが起こっていることがわかっているときにAが起こる確率を条件付き確率と呼び、\(P(A\mid B)\)と表現されています。このような話題を考えるときに、ベイズ理論は役立ちます。

実際、スパムメールのフィルタリングには、ベイジアンフィルタというものが使われています。

論理学

機械が人間の言葉を読むためには、自然言語処理と呼ばれる分野が役立ちます。

文章を読み取って問題を解かせたいなら、文字の列を文として認識させるだけでなく、そこに含まれる論理を読み解く必要があります。

そこでコンピュータに論理を教えるために使われるのが、記号論理・数理論理学です。

境界分野

大学の数学科の授業で扱われることは少ないが、数学を使って理論化された分野が人工知能の理論では使われています。

例えば、ゲーム理論、ベイズ理論・ベイズ統計学、グラフ理論、最適化数学・数理計画法などがそうですね。

それぞれ教科書があるような大きな分野なので、探してみると良いでしょう。

まとめると、人工知能・機械学習を学ぶには、線形代数学、微積分学、確率論の知識があったほうが良いでしょう。

「パターン認識と機械学習」は、その英題からPRMLと呼ばれ、機械学習のバイブルとなっていますが、難しいと評判です。

「イラストで学ぶ人工知能概論」はかなり読みやすかったので、数学の基礎を固める前に読んでみて、そこでよくわからなかったパートの数学を学べば良いと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。