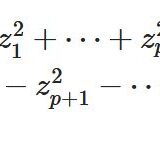正方行列は上三角化可能であることの例、証明

どうも、木村（@kimu3_slime）です。

任意の正方行列\(A\)は、適切に可逆行列\(P\)を選ぶことで\(P^{-1}AP=U\)が上三角行列であるように変形できます。この条件を上三角化可能であると呼びましょう。

まずはそのような上三角化の例を紹介し、その後に一般的な証明をします。

上三角化の例
上三角化の証明
こちらもおすすめ

上三角化の例

\[ \begin{aligned}A= \frac{1}{2} \begin{pmatrix} 13&-1 \\ 9&7\end{pmatrix}\end{aligned} \]

という正方行列を題材としましょう。

三角化の手順は、対角化と同様、固有値・固有ベクトルを利用します。

まず、特性多項式\(\det (\lambda I-A)=0\)は

\[ \begin{aligned} &(\lambda-\frac{13}{2})(\lambda -\frac{7}{2})+\frac{9}{4} \\ &=(\lambda-5)^2 \end{aligned} \]

となり、\(\lambda =5\)が代数的重複度2の固有値です。

対応する固有ベクトルを求めるために基本変形すると

\[ \begin{aligned} &A-5I\\&= \frac{1}{2} \begin{pmatrix} 3&-1 \\ 9&-3\end{pmatrix} \\ & \sim\frac{1}{2} \begin{pmatrix} 3&-1 \\ 0&0\end{pmatrix} \end{aligned} \]

となるので、固有ベクトルのひとつは\(p_1=(1,3)\)しか見つかりません。

固有空間の次元が1で、それが代数的重複度2と等しくないので、行列\(A\)を対角化することはできません。

参考：行列の対角化可能性と同値な条件とは：証明、判定法

しかし、この行列を上三角化することはできます。

\(e_1,e_2\)を標準基底としましょう。そして\(p_2 =e_2\)とすると、\(p_1,p_2\)は線形独立なので、それらを列ベクトルとして並べた行列\(P=(p_1,p_2)\)は可逆行列です。

\(AP =PU\)の形となるように計算してみましょう。

\[ \begin{aligned} AP &= \begin{pmatrix} Ap_1 &Ap_2 \end{pmatrix} \\&= \begin{pmatrix} 5p_1 &Ap_2\end{pmatrix} \\ &= P\begin{pmatrix} 5e_1 &P^{-1}Ap_2\end{pmatrix}\end{aligned} \]

となるので、

\[ \begin{aligned}P^{-1}AP =\begin{pmatrix} 5e_1 &P^{-1}Ap_2\end{pmatrix}\end{aligned} \]

と上三角行列にすることができました。成分を具体的に計算すると

\[ \begin{aligned}P^{-1}AP = \begin{pmatrix} 5& -\frac{1}{2}\\ 0&5 \end{pmatrix}\end{aligned} \]

となります。対角成分には、固有値が重複度の個数分だけ並んでいますね。

上三角化の過程では、\(p_1\)は固有ベクトルとして選びましたが、\(p_2\)は固有ベクトルでもなんでもありません。\(p_1\)と線形独立ならなんでも良いです。

さらにここで\(p_2\)の選び方を工夫する（一般固有ベクトルとして選ぶ）ことで、ジョルダン標準形と呼ばれる上三角行列が得られます。ジョルダン標準形の基礎としても、まずは行列が上三角化できることを知り納得しておくと良いでしょう。

参考：なぜジョルダン標準形を考えるか、求め方、一般固有ベクトル

上三角化の証明

では、一般的な主張を述べて、証明しましょう。

\(A\)を\(N\)次の複素正方行列とする。

このとき、ユニタリ行列\(P\)（\(\overline{P}^\top P =I\)を満たす行列）と上三角行列\(U\)で、\(P^{-1} AP =U\)を満たすものが存在する。さらに、\(U\)の対角成分には\(A\)の固有値が重複込みですべて並ぶようにできる。

言い換えると、任意の正方行列は上三角行列に相似である。

特に、\(A\)の固有値がすべて実数のときは、直交行列によって上三角化できる。

注意したいのが、\(A\)の成分がすべて実数だったとしても、できあがる上三角行列がすべて実数にできるとは限りません。固有値、固有ベクトルは一般に複素数になるので。

では、証明してみましょう。

行列のサイズ\(N\)に関する帰納法で示します。

\(N=1\)のときは、成分が何であろうが対角行列であり、既に上三角行列となっています。また、その対角成分は固有値でもあります。

\(N=k\)のとき、上三角化可能であり、対角成分に固有値が重複込みで並んでいると仮定しましょう。\(k+1\)次の正方行列\(A\)が上三角化可能であることを示します。

\(A\)の固有値のひとつを\(\lambda_1\)、対応する固有ベクトルを\(q_1\)とします。\(q_1 \neq 0\)なので、そのノルム\(\|q_1\|\)で割ることで\(\|q_1\|=1\)と正規化することができるので、既にそうなったものを\(q_1\)としましょう。

\(\mathbb{C}^{k+1}\)（実数成分で考えるときは\(\mathbb{R}^{k+1}\)）の次元は\(k+1\)なので、\(q_1\)に対して\(q_1,q_2,\dots,q_{k+1}\)が線形独立であるような\(q_2,\dots,q_{k+1}\)が存在します（線形独立であるなら何でも良い）。さらに、これらに（複素内積に関する）シュミットの直交化法を適用して、\(q_1,\dots,q_{k+1}\)が正規直交基底であるようにできます。

\(Q= (q_1,\dots,q_{k+1})\)と列ベクトルを並べた行列を考えます。\(Q\)は正規直交基底を並べた行列なので、ユニタリ行列です。そして\(AQ\)を計算しましょう。

\[ \begin{aligned} AQ &=(Aq_1,Aq_2\dots,Aq_{k+1})\\ &=(\lambda_1 q_1,Aq_2\dots,Aq_{k+1})\\ &= Q \begin{pmatrix} \lambda_1 &*\\ 0 &A_k \end{pmatrix}\end{aligned} \]

ここで\(A_k\)は\(k\)次の正方行列です。帰納法の仮定より、\(R_{k}^{-1}A_k R_{k} = U_{k}\)なるユニタリ行列\(R_k\)、対角成分に固有値が並んだ上三角行列\(U_k\)が存在します。

ここで\(A\)が三角化できるように、

\[ \begin{aligned} R=\begin{pmatrix}1 &0^\top \\0& R_k \end{pmatrix}\end{aligned} \]

と置きます（\(0\)は適切なサイズ＝\(k\)次のゼロベクトル）。すると、

\[ \begin{aligned} (QR)^{-1}AQR&= R^{-1}Q^{-1}AQ R\\&= \begin{pmatrix}1 &0^\top \\0& R_k^{-1} \end{pmatrix} \begin{pmatrix} \lambda_1 &*\\ 0 &A_k \end{pmatrix}\begin{pmatrix}1 &0^\top \\0& R_k\end{pmatrix}\\ &= \begin{pmatrix}1 &0^\top \\0& R_k^{-1} \end{pmatrix} \begin{pmatrix} \lambda_1 &*\\ 0 &A_k R_k \end{pmatrix}\\ &= \begin{pmatrix} \lambda_1 &*\\ 0 &R_{k}^{-1}A_k R_k \end{pmatrix} \\ &= \begin{pmatrix} \lambda_1 &*\\ 0 &U_k\end{pmatrix}\end{aligned} \]

と上三角行列になります。ここで\(P=QR\)は、ユニタリ行列の積なのでユニタリ行列です。

また、対角成分には\(A\)の固有値が重複込みですべて並んでいます。ちなみに、重複する固有値を隣の列に置くことができます。

\(A\)の固有値がすべて実数のときは、固有ベクトルもすべて実成分になります。したがって、ユニタリ行列は単に直交行列です。

上三角化の手順を要約すると、次のようになります。

まずひとつの固有値、固有ベクトルを使えば、

\[ \begin{aligned}Q^{-1}AQ=\begin{pmatrix} \lambda_1 &*\\ 0 &A_k \end{pmatrix}\end{aligned} \]

と第1行を固有値\(\lambda_1\)が対角成分にあり他が0であるようにできます。\(Q\)の列ベクトルは、ひとつは固有ベクトルで、他はそれと線形独立なベクトルを並べます。上三角行列にするのが目標なので、線形独立ならばなんでも良いです。簡単に計算できそうなものを選ぶと良いでしょう。\(Q\)をユニタリ行列として選びたいなら、シュミットの直交化法で直交化しておきましょう。

ここでさらに、上三角化されていないブロック行列\(A_k\)に注目し、\(A_k\)の固有ベクトルをひとつだけ取って、その最初の行に固有値が出てくるようにする。こうした手順を繰り返していけば良いわけです。

\[ \begin{aligned} R=\begin{pmatrix}1 &0^\top \\0& R_k \end{pmatrix}\end{aligned} \]

のような行列を使えば、既に上三角化が済んだ\(\lambda_1\)の部分に影響を与えずに、\(A_k\)のみを上三角化することができます。

任意の行列が上三角化可能という結果は、正規行列が対角化可能、実対称行列が対角化可能という結果に応用できます。

ジョルダン標準形の一般的な証明でも利用するので、対角化やジョルダン標準形を支える基本的な事実と言えるでしょう。

参考：対称行列の性質：内積による特徴づけ、逆行列、固有値、対角化について

以上、正方行列は上三角化可能であることの例、証明を紹介してきました。

行列のべき乗計算をする上では、対角化ができるなら対角化をして、対角化できないときはジョルダン標準形を考えることが多いでしょう。

上三角化の手順に慣れるよりは、より優れた上三角行列：ジョルダン標準形の手順に慣れる方が実用的でしょう。

それでも、それらの対角化やジョルダン標準形を支える基本的な事実として、どんな行列も上三角化できると知っておくのは大事だと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。