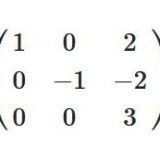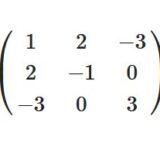どうも、木村(@kimu3_slime)です。
今回は、サラスの方法、行列式の覚え方として、置換を使った定義を理解するための解説をしようと思います。
サラスの方法とは
そもそも行列式(determinant)とは、行列が可逆行列かどうか、逆行列を持つかどうかを判定するための量のことです。\(\det A \neq 0\)と、可逆行列であることは同値になります。
さて、行列式が0でないかどうかを確かめるには、実際に行列式を計算する必要があります。
サラスの方法(Rule of Sarrus)、またはサラスの展開とは、2次・3次の行列式の計算方法、覚え方のことです。
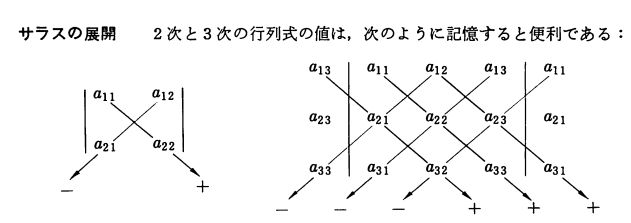
画像引用:明解演習 線形代数
\(A=(a_{ij})\)とするとき、2次、3次の行列式は
\[ \begin{aligned}\det A = a_{11}a_{22}-a_{12}a_{21}\end{aligned} \]
\[ \begin{aligned}\det A =a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}\\-a_{11}a_{23}a_{32}- a_{13}a_{22}a_{31}- a_{12}a_{21}a_{33}\end{aligned} \]
となります。このプラスまたはマイナスがかかった積の式を覚えるための方法が、サラスの方法です。上の図のように矢印を引いて足し合わせていけば良い、と。
線形代数学の試験では、行列式の計算はよく出題されることもあり、3次の行列式を覚えた方もいるのではないでしょうか。
僕個人としては、2次の行列式は簡単なので覚えて良いですが、3次のものを覚える必要はないと思っています。なぜなら、余因子展開をして2次の行列式に帰着させていくほうが簡単で、間違いが少ないからです。
また、線形代数の応用を目的とするなら、具体的な行列の行列式はコンピュータで求めれば良いものです。機械的な計算のトレーニングには、それほど深い教育的意義はないのではないかと思っています。
それでも、僕はサラスの展開について線形代数学の講義で触れることには意味があると思っています。
- 実際に計算してみると面倒くさい→工夫(余因子展開)が必要と学ぶ
- 3次に限らず、n次の行列式の一般形(置換を使った定義)を知ることにつながる
今回は、後者をについて、できるだけ簡単なところから具体的に紹介していこうと思います。
置換を使った行列式の定義
2次の行列式
行列式の一般的な定義には、置換というものが使われます。
2次の行列は、
\[ \begin{aligned}\det A = a_{11}a_{22}-a_{12}a_{21}\end{aligned} \]
と表されますが、置換の言葉を使うと
\[ \begin{aligned}\det A := \sum_{\sigma \in S_2} \mathrm{sgn}(\sigma)a_{\sigma(1)1}a_{\sigma(2)2}\end{aligned} \]
と表されます。置換\(\sigma\)は、成分番号の入れ替えの規則を表すものです。
\(S_2\)は、2次の置換全体からなる集合を表します。その要素である置換\(\sigma\)とは、\(\{1,2\}\)という2つの数を、\(\{1,2\}\)のいずれかに重複なしに割り当てる関数のことです。
\(\sum_{\sigma \in S_2}\)は、2次の置換\(\sigma\)すべてに渡って足し合わせることを意味します。数列のように番号づけられていませんが、いくつかの和、有限個の和です。
\(S_2\)には、\(e,\sigma_1\)という2つの要素しかありません。2個の和になります。
\(e(1)=1,e(2)=2\)によって定まる置換は、何も入れ替えないため、恒等置換と呼ばれます。\(\sigma_1(1)=2,\sigma_2(2)=1\)は、2つの数の入れ替えをしています。この記号を使うと、行列式の定義に登場する積が、次のように表されることがわかるでしょうか。
\[ \begin{aligned}a_{11}a_{22} = a_{e(1),1}a_{e(2),2}\end{aligned} \]
\[ \begin{aligned}a_{12}a_{21}= a_{\sigma_1(1), 1}a_{\sigma_1 (2), 2}\end{aligned} \]
おおざっぱに視覚的に言えば、行列式とは次のように積を作って足したものと言えます。
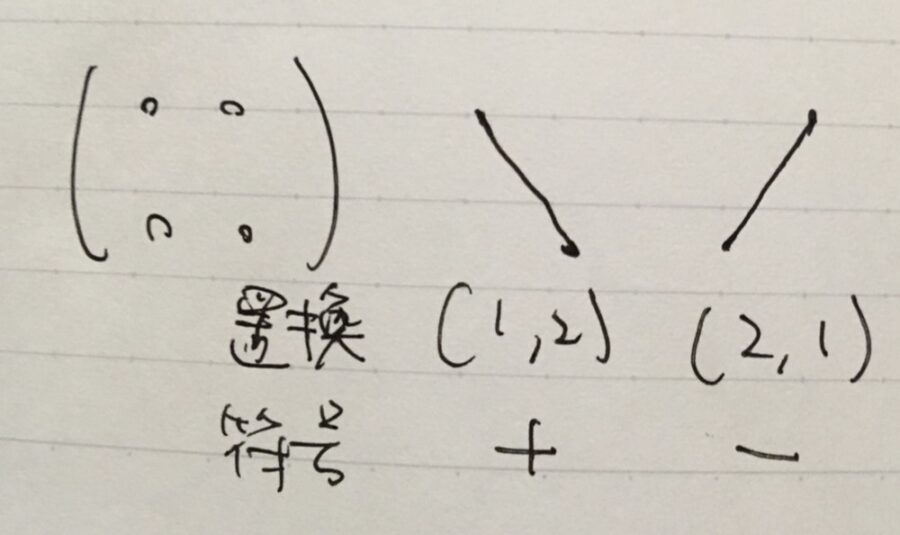
つまり、第1列から何か成分、例えば\(a_{11}\)を選ぶ。そしたら、第2列から何か成分を選ぶが、\(a_{11}\)と行がかぶってはいけない。なので、\(a_{22}\)を選ばざるを得ない。そうして積\(a_{11}a_{22}\)を得る。第1列で\(a_{21}\)を選んだら、\(a_{21}\)を選ばざるを得ない。
\(1,2\)という番号から、重複なしに順番を考慮した列(順列)を作る。すると、\(e=\begin{pmatrix} 1 & 2 \end{pmatrix}\)か\(\sigma_1 =\begin{pmatrix} 2 & 1 \end{pmatrix}\)の2通りができる。こうした重複のない列による数の対応規則\(\sigma\)を、置換(permutation)と呼んでいます。
重複のない列を作る、というのがポイントです。行列式には、\(a_{11}a_{12}\)のような列番号が同じ積は登場しないのです。それは\(1,1\)という重複ありの列を考えることに対応しています。行について考えても同様で、\(a_{22}a_{12}\)という積は登場しません。
(高校では、\(n\)文字から\(k\)文字を選ぶ置換の総数(順列)\(_n P_k\)を学びます。このPは置換 permutation のPです。今回考える置換というものは、\(n\)文字から\(n\)文字を選ぶ順列で、一般に\(_n P _n =n!\)通りあります。)
さて、行列式とは、単に和を取るだけでなく、プラスマイナスをかけていました。
\[ \begin{aligned}\det A := \sum_{\sigma \in S_2} \mathrm{sgn}(\sigma)a_{\sigma(1)1}a_{\sigma(2)2}\end{aligned} \]
すべての置換には符号というものが定まっていて、それを\(\mathrm{sgn}(\sigma)\)と表します。
恒等置換の符号はプラスで、\(\mathrm{sgn}(e)=+1\)とします。
一般の場合の符号は、その置換の2つの数を入れ替える操作によって恒等置換に変形するとき、その入れ替えの回数によって決まります。偶数回ならプラス、奇数回ならマイナスです。
\(\sigma_1 =\begin{pmatrix} 2 & 1 \end{pmatrix}\)を\(e=\begin{pmatrix} 1 & 2 \end{pmatrix}\)に変形させるには、1回数を入れ替える必要があります。奇数回の交換なので、\(\mathrm{sgn}(\sigma) = -1\)です。
以上によって、
\[ \begin{aligned} \det A &= \sum_{\sigma \in S_2} \mathrm{sgn}(\sigma)a_{\sigma(1)1}a_{\sigma(2)2} \\ &= \mathrm{sgn}(e)a_{e(1)1}a_{e(2)2} \\&+\mathrm{sgn}(\sigma_1)a_{\sigma_1(1)1}a_{\sigma_1(2)2} \\ &=a_{11}a_{22}-a_{12}a_{21}\end{aligned} \]
となることがわかりました。
置換と符号を使った定義は、最初は面倒くさいと感じるでしょうが、一般の行列式について同様の議論ができるのが便利です。
3次の行列式
3次の行列式を
\[ \begin{aligned}\det A := \sum_{\sigma \in S_3} \mathrm{sgn}(\sigma)a_{\sigma(1)1}a_{\sigma(2)2} a_{\sigma(3)3}\end{aligned} \]
という置換を使った定義にのっとって計算してみましょう。\(S_3\)は3次の置換のなす集合です。
まず、3次の置換は\(3! =6\)個あります。それを次の図のように、書き出して列挙してみましょう。
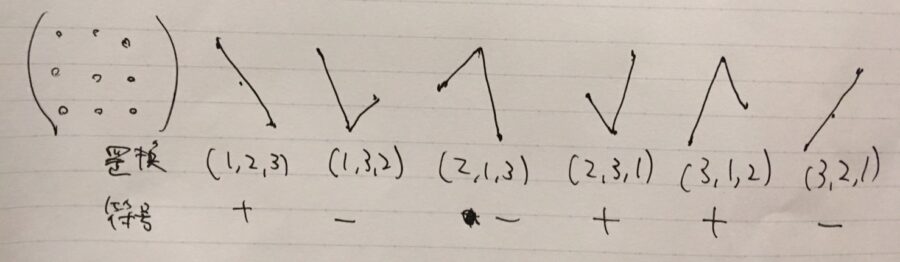
樹形図や場合分けの考え方で書き出しています。第1列から1を使うなら、2,3列では\(2,3\)と\(3,2\)の可能性がある、といったように。
\(\begin{pmatrix} 2 & 3 &1\end{pmatrix}\)という記号は、\(\sigma(1)=2\)、\(\sigma(2)=3\)、\(\sigma(3) =1\)という置換を省略して書いたものです(置換の一行記法)。
\[ \begin{aligned}\sigma =\begin{pmatrix} 1 & 2 & 3\\ 2& 3& 1 \end{pmatrix}=\begin{pmatrix} 2 & 3 &1\end{pmatrix}\end{aligned} \]
そして、それぞれの符号を計算してみます。恒等置換\(e=\begin{pmatrix} 1 & 2 &3\end{pmatrix}\)にするのに、2個の数字の入れ替えを何回するかを数え、その偶奇によって判定するわけです。
\[ \begin{aligned}\mathrm{sgn}\begin{pmatrix} 1 & 2 &3\end{pmatrix} =1\end{aligned} \]
\[ \begin{aligned}\mathrm{sgn}\begin{pmatrix} 1 & 3 &2\end{pmatrix} =-1\end{aligned} \]
\[ \begin{aligned}\mathrm{sgn}\begin{pmatrix} 2& 1 &3\end{pmatrix} =-1\end{aligned} \]
\[ \begin{aligned}\mathrm{sgn}\begin{pmatrix} 2 & 3 &1\end{pmatrix} =1\end{aligned} \]
\[ \begin{aligned}\mathrm{sgn}\begin{pmatrix}3 & 1 &2\end{pmatrix} =1\end{aligned} \]
\[ \begin{aligned}\mathrm{sgn}\begin{pmatrix}3 & 2 &1\end{pmatrix} =-1\end{aligned} \]
例えば、\(\begin{pmatrix} 2 & 3 &1\end{pmatrix} \)の符号は次のように考えて計算しています。1回入れ替えると、\(\begin{pmatrix} 3 & 2 &1\end{pmatrix} \)で、もう1回入れ替えると\(\begin{pmatrix} 1 & 2 &3\end{pmatrix} \)。入れ替えの回数は2回、偶数回なので、符号はプラスである、と。
この置換と符号の書き出しの結果によって、行列式の定義を展開することができます。上の置換、符号と順序を対応させているので、見比べてみてください。
\[ \begin{aligned} \det A &= \sum_{\sigma \in S_3} \mathrm{sgn}(\sigma)a_{\sigma(1)1}a_{\sigma(2)2} a_{\sigma(3)3}\\ &=+a_{11}a_{22}a_{33}-a_{11}a_{32}a_{23} \\ &-a_{21}a_{12}a_{33}+a_{21}a_{32}a_{13} \\ &+a_{31}a_{12}a_{23}-a_{31}a_{22}a_{13} \\&=a_{11}a_{22}a_{33}+ a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32} \\ &-a_{11}a_{23}a_{32}- a_{13}a_{22}a_{31}- a_{12}a_{21}a_{33}\end{aligned} \]
最後の等式は、符号が同じ項をまとめ、積の順序を入れ替えたものです。サラスの方法そのものである結果が得られました。
n次の行列式
一般の行列式は、次のように定義されます。
\[ \begin{aligned}\det A := \sum_{\sigma \in S_N} \mathrm{sgn}(\sigma)a_{\sigma(1)1}a_{\sigma(2)2} \cdots a_{\sigma(N)N}\end{aligned} \]
\(S_N\)は\(N\)次の置換全体のなす集合(\(N\)次の対称群)です。
いくつもの積があるので、積の記号\(\prod\)を使って
\[ \begin{aligned}\det A := \sum_{\sigma \in S_N} \prod _{i=1}^N \mathrm{sgn}(\sigma)a_{\sigma(i)i}\end{aligned} \]
と書くことも。置換を使って成分をかけて足し合わせているだけなので、ビビらないように。
今回の話では、列\(i\)に対して行\(\sigma(i)\)を選んでいましたが、行に対して列を選んでも全く同じ定義になります。
\[ \begin{aligned}\det A := \sum_{\sigma \in S_N} \prod _{i=1}^N \mathrm{sgn}(\sigma)a_{i\sigma(i)}\end{aligned} \]
いかめしい定義ですが、置換を使った行列式の定義を理解していると、3次以上の行列の行列式でもすぐに計算できることがわかります。
その典型例は、対角行列や三角行列です。
\[ \begin{aligned}D=\begin{pmatrix} d_1 &0& &O \\ 0& d_2 & & \\ &\ddots & \\ O & & &d_N \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\det D = d_1 d_2 \cdots d_N\end{aligned} \]
\[ \begin{aligned}U=\begin{pmatrix} u_{11} & *&*\\ 0& u_{22} & & \\ &\ddots & \\ O & & &u_{NN} \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\det U = u_{11} u_{22} \cdots u_{22}\end{aligned} \]
なぜこうなるかわかりますか? 2次、3次の行列でやったように、行列に線を書きながら、置換の候補を考えてみると良いでしょう。対角成分を選ぶ置換(恒等置換)以外では、積に0が登場してしまうので、そのような置換の部分は計算しなくて良いのです。
参考:対角行列の性質:積、逆行列、固有値について、上三角、下三角行列の性質:積、逆行列、固有値について
形の上での規則性がなくても、各列に1つしか成分がないような置換行列
\[ \begin{aligned}P=\begin{pmatrix} 0& 1&0\\0 & 0&1 \\ 1&0&0 \end{pmatrix}\end{aligned} \]
についても、置換による行列式の定義がわかっていれば、\(\det P=1\)と秒でわかるでしょう(一般には、行列式は1または-1)。行列式が-1になるような4次、5次の行列の例を作ってみてください。
また、「ある列が0ベクトルとなるような行列を考えると、その行列式は0となること」は明らかに思えるでしょうか?
\[ \begin{aligned}\det A := \sum_{\sigma \in S_N} \mathrm{sgn}(\sigma)a_{\sigma(1)1}a_{\sigma(2)2} \cdots a_{\sigma(N)N}\end{aligned} \]
その列を\(k\)列としましょう。どんな置換を考えても、\(a_{\sigma(k)k}\)が0になるので、\(\det A=0\)です。同様の主張は、列でなく行についても言えますね。
以上、サラスの方法、行列式の覚え方として、置換を使った行列式の定義について紹介してきました。
行列式の具体的な計算を行う上では、余因子展開の方が簡単なことが多いです。ただ、置換を使って行列式を捉え直すと、サイズの大きな一般的な行列であっても、簡単に計算できる場合があることがわかります。
サラスの方法の形だけを覚えようとするのでなく、ついでに置換を使った行列式の定義の議論を一度追って見ると、行列式の本質に迫れるのではないかと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版 (1982-07-09T00:00:01Z)
¥788 (中古品)
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社 (2015-12-22T00:00:01Z)
¥14,721 (コレクター商品)
東京大学出版会 (2019-03-08T00:00:00.000Z)
¥1,870
こちらもおすすめ
なぜ行列式を学ぶのか? 固有値・固有ベクトルの求め方:固有多項式の定義