なぜ平行でないベクトルによる分解を考えるか：線形独立とは

どうも、木村（@kimu3_slime）です。

高校数学のベクトルの分野では、2つの平行でないベクトルがあると、あらゆるベクトルがその2つによって分解できる\(x = sa +t b\)、という話があります。

なぜこんな問題を考えるのでしょうか。これは大学数学、線形代数学にかかわってくる話で、特に線形独立、基底という考え方について紹介します。

ベクトルが平行性と分解
平行でないことの一般化：線形独立
こちらもおすすめ

ベクトルが平行性と分解

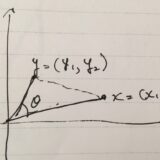
簡単のため、平面における（位置）ベクトルを考えましょう。

2つのベクトル\(a,b\)が平行であるとはどういうことでしょうか。

例えば、\(a=(1,1)\)と\(b=(3,3)\)は平行です。\(a\)を向きにしてそのまま大きさを伸ばせば、\(b\)にぴったり重なります。つまり、\(b= 3a\)と表せます。

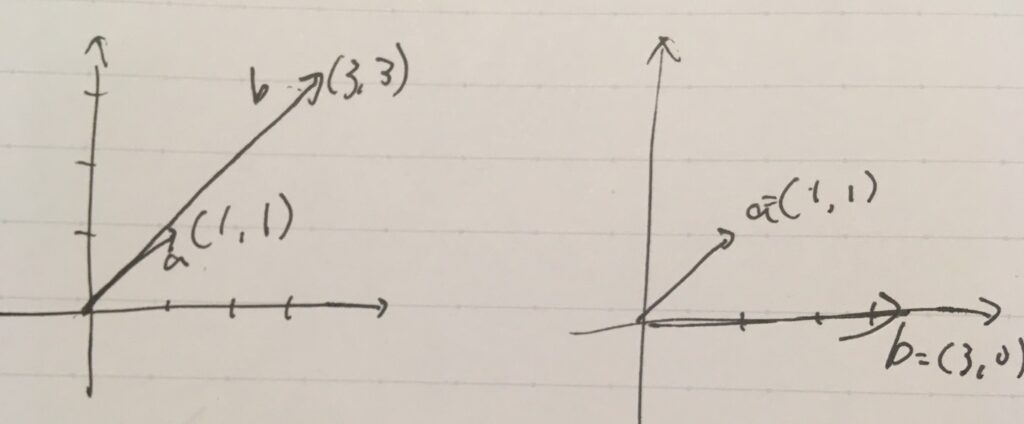
一方で、\(a=(1,1)\)と\(b=(3,0)\)は平行ではありません。\(a\)をどんなに拡大縮小しても、第2成分が0になることは決してありませんよね。これは\(b=k a\)となる実数\(k\)が存在しない、と言いかえられます。

一般的に考えましょう。2つのベクトル\(a,b\)の成分を\(a=(a_1,a_2)\)、\(b=b_1,b_2\)とします。\(a,b\)が平行であるとは、\(b= ka\)を満たす実数\(k\)が存在すること。\(a,b\)が平行でないとは、どんな実数に対しても\(b=ka\)が成り立たないこと、と定義しましょう。

ベクトルの平行の考え方を導入すると、どんな良いことがあるのでしょうか。よく知られた性質が、ベクトルの分解です。

平面において、2つの平行でなく、0ベクトルでないベクトル\(a,b\)があると、あらゆるベクトル\(x\)をその2つのベクトルで分解することができます。つまり、\(x= sa +tb\)を満たす実数\(s,t\)が存在します。

これは本当なのでしょうか？　試してみましょう。

\(x= (5,2)\)とします。\(a=(1,1)\)と\(b=(3,0)\)は、互いに平行ではありません。\(x =sa +tb\)と置いてみましょう。成分を計算すれば、\(5 = s+3t\)、\(2 = s+0t\)です。つまり、\(s=2,t=1\)と置けば良く、\(x=2a +b\)と確かに分解できました。

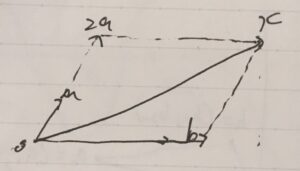
この性質は、\(a,b\)が平行でないと、必ずしも成り立ちません。例えば、\(x= (5,2)\)を、\(a=(1,1)\)と\(b=(3,3)\)の平行なベクトルで分解しようと考えてみましょう。\(b= 3a\)であったことを思い出すと、\(sa+tb =(s+3t)a\)となります。これが\(x\)に等しいとすると、各成分の比較から、\(5 =s+3t \)、\(2 =s+3t\)となります。これを満たす実数\(s,t\)は存在しません（存在したら、\(5=2\)が導かれてしまう）。

ただし、平行でないと必ず他のベクトルを表現できないと言っているわけではないことに注意しましょう。例えば\(x=(2,2)\)は\(x= 2a +0b\)と表せます。しかし\(x=(5,2)\)のように表現できないベクトルも一般にはある、という話です。

これを発展させた話題として、分解の方法が1通りであること（一意性）もあります。

平面において、2つの平行でなく、0ベクトルでないベクトル\(a,b\)があり、\(x\)を任意のベクトルとする。係数\(s,t,u,v\)が\(x= sa +tb= ua +vb\)を満たすならば、\(s=u,t=v\)が必ず成り立つ。

この結論は、\(a,b\)が平行でなければ必ずしも成り立ちません。

例えば、\(x=(4,4)\)というベクトルを、2つの\(a=(1,1)\)と\(b=(3,3)\)ベクトルで分解してみます。すると、\(x= a+b= -2a+2b\)といったように、2通り（以上）に表すことができます。

平行でないことの一般化：線形独立

ここまでの話には、大学数学、線形代数学で扱う考え方が背景にあります。それを簡単に紹介しましょう。少し用語をつけると、問題のイメージがしやすくなるかと。

2つのベクトル\(a,b\)があるとき、\(sa+t b\)という式をよく考えました。\(s,t\)という実数を調整することで、\(a,b\)を伸ばしたり縮めたり、向きを変えたりできて、いろいろなベクトルが表現できないか考えます。

ベクトル\(a,b\)を定数倍でつなぎあわせた\(sa+ tb\)を、\(a,b\)の線形結合（linear combination）、一次結合と呼びます。\(k_1 a+k_2 b\)と係数を表す文字を変えても、同じです。

「\(a,b\)が平行でなく、0ベクトルでない」という条件もよく登場しました。まだるっこしいので、これにも名前をつけてしまいましょう。

\(sa+tb =0\)ならば、必ず\(s=t=0\)が成り立つとき、\(a,b\)は線形独立（linearly independent）、一次独立であると言います。これは\(a,b\)が平行でなく、0ベクトルでないことの言い換えになっています。

「平行でなく、0ベクトルでない」ならば線形独立
- \(a,b\)を平行でないと仮定して、\(sa+tb =0\)が成り立つとしましょう。\(t\neq 0\)のときは、\(b= \frac{-s}{t}a\)と変形できますが、これは\(a,b\)が平行でないことに矛盾します。したがって\(t=0\)です。また\(a\)が0ベクトルでないなら、\(sa =0\)より\(s=0\)が導かれます。
線形独立ならば、「平行でなく、0ベクトルでない」
- \(a,b\)を線形独立と仮定します。背理法として、\(a,b\)が平行であると仮定しましょう。すると、\(b= ka \)を満たす実数が存在します。これは\(ka -b =0\)を満たしますが、これは線形独立の仮定に矛盾します。よって、平行でないと言えました。
- \(a\)が0ベクトルとすると、\(1 a +0b =0\)が成り立ち、これは線形独立性に矛盾します。\(b\)についても同様で、どちらも0ベクトルでないと言えました。

\(a,b\)が線形独立でないことを、線形従属（linearly dependent）、一次従属であると呼びます。条件としては、\(sa+tb =0\)を満たす、両者が0ではない実数\(s,t\)が存在すること。

線形従属は、「平行であるか、一方が0ベクトルである」ことの言い換えになっています。例えば、\(a =3b\)という関係がある（平行な）ときは、\(s=1,t=-3\)として\(sa+tb=0\)が成り立ち、\(a,b\)は線形従属でありません。

以上の考え方を使うと、ベクトルの分解の性質が簡単に述べられます。

平面において、\(a,b\)を線形独立なベクトルとする。\(x\)を任意のベクトルとする。このとき、\(x= sa+tb\)と線形結合で1通りに表すことができる。

「平行でなく、0でないベクトルを考える」というと、なぜそんな条件を考えるのかと思うかもしれませんが、それは一般的なベクトル\(x\)を\(a,b\)で分解しようとするとき、\(a,b\)が独立な関係にあることを示していたのです。

主張を証明してみましょう。

\(x= sa+tb\)と表せること
- \(a,b\)が線形独立であることと、さきほど示したことから、\(a,b\)は0ベクトルではありません。\(a=(a_1,a_2),b=(b_1,b_2)\)と成分表示します。
- \(x= (x_1,x_2)\)とします。\(x_1 =sa_1 +tb_1\)、\(x_2 = sa_2 +tb_2\)を満たす\(s,t\)を作りたいです。仮に\(a_1 \neq 0\)なら、\(s=\frac{1}{a_1}(x_1-tb_1)\)と表わせます。これを代入すれば、\(x_2 =\frac{a_2}{a_1}(x_1-tb_1)+tb_2\)です。これを解くと、仮に\(a_1b_2-a_2b_1 \neq 0\)ならば、\(t=\frac{a_1 x_2 -a_2 x_1}{a_1b_2-a_2b_1} \)と表せます。そして\(s= \frac{b_2 x_1 -b_1 x_2}{a_1b_2-a_2b_1}\)と表せます。
- \(a_1 =b_1=0\)となることはありえません。なぜなら、そのときは\(a+ \frac{-a_2}{b_2}b=(0,a_2 -a_2)=0\)となります（\(a,b\)は0ベクトルでないので\(b_2 =0\)となることはない）。これは\(a,b\)が線形独立になることに矛盾します。したがって、\(a_1,b_1\)の一方は0ではありません。上の議論は\(a_1 \neq 0\)としましたが、\(b_1 \neq 0\)で同様に議論できます。
- \(a_1b_2-a_2b_1 \neq 0\)となることを示しましょう。背理法として、\(a_1b_2-a_2b_1 = 0\)と仮定します。すると、成分を計算して\(a =\frac{a_1}{b_1}b \)が成り立ちます。これは\(a,b\)が線形独立であること、平行でないことに矛盾しました。
\(x= sa+tb\)の表現が1通りであること
- \(sa+tb= ua+vb\)と2通りに表されたと仮定する。これを整理すれば、\((s-u)a+(t-v)b=0\)で、\(a,b\)の線形独立性から\(s-u=0,t-v=0\)。よって、\(s=u,t=v\)と1通りであることが言えました。

このベクトルの分解の主張は、\(a,b\)が基底であること、平面は2次元であるといった用語で説明される内容です。途中でできた分母\(a_1b_2-a_2b_1\)は、行列式と呼ばれるもの。詳しく述べると長くなるので、例えば次の記事を参照。

参考：実数空間、線形結合、線形部分空間、次元とは何か：2次元を例に、可逆な行列（正則行列）とは？例と同値な条件

「平行でない・である」から、「線形独立・線形従属」という用語を考えることで、平面だけでなく、空間のベクトル、4次元以上のベクトルについても同様の性質を考えることができます。

空間において、\(a,b,c\)を線形独立なベクトルとする。\(x\)を任意のベクトルとする。このとき、\(x= sa+tb+uc\)と線形結合で1通りに表すことができる。

内積の考え方を使うと、線形独立かどうかが計算によって判定できます。2つのベクトルの内積が0になる＝垂直な関係ならば（直交するならば）、互いに線形独立といった性質があります。興味のある人は調べてみてほしい。

参考：直交ベクトルの線形独立性、直交行列について解説

以上、平行でないベクトルが2つによってベクトルが分解できるのはなぜか、線形独立という考え方を紹介してきました。

複雑な要素を持ったベクトル\(x\)を、よく知られた単純なベクトル\(a,b\)に分解する（\(x\)を\(a,b\)の線形結合で表す）という考え方は、数学やその応用で役に立ちます。たとえば、複雑な関数を三角関数に分解するフーリエ級数の考え方など。

高校数学では、ベクトルが平行だの平行でないだの面倒くさいことを気にするな、と思うかもしれません。しかし、今回の話で、「ベクトルの分解やそのための条件」は重要で、そのための名前がついていることを知ってもらえたら嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。