どうも、木村(@kimu3_slime)です。
高校数学の確率の分野では、組み合わせ、二項係数\(_n C _k\)が登場します。\(_n C_ k = \frac{n!}{k!(n-k)!}\)となるわけですが、僕はこの公式を覚えるのに苦戦した記憶があります。
ということで、今回は組み合わせ・二項係数\(_n C _k\)の公式の覚え方、パスカルの三角形を紹介していきましょう。
パスカルの三角形
\(_n C_ k = \frac{n!}{k!(n-k)!}\)という公式は、いきなり一般形として覚えようとするから難しいのです。まずは、\(n,k\)が\(2,3,4\)といった小さい数のときにどういう値を取るのか、それを意識しておくと良いでしょう。
\(_n C_k\)は、高校数学ではまず組み合わせの数として導入されるかもしれませんが、それには二項係数という別名があります。
どうしてそんな名前があるのか、2つの項のべき乗\((x+1)^n\)の展開式の係数を考えてみましょう。
\[ \begin{aligned}(x+1)^2 =x^2 +2x +1\end{aligned} \]
\[ \begin{aligned}(x+1)^3 = (x+1)(x^2+2x+1)\\=x^3 +3x^2 +3x +1\end{aligned} \]
\[ \begin{aligned}(x+1)^4 = (x+1)(x^3+3x^2+3x+1)\\=x^4+4x^3 +6x^2+4x+1\end{aligned} \]
と地道に計算すれば得られます。ここで登場している係数が、二項係数\(_n C _k\)(binomial coefficient)です。
\[ \begin{aligned}(x+1)^2 = _2C_0 x^2 +_2C_1x +_2C_2 1\end{aligned} \]
\[ \begin{aligned}(x+1)^3 =_3 C_0x^3 +_3 C_1x^2 +_3 C_2x +_3 C_3 1\end{aligned} \]
\[ \begin{aligned}(x+1)^4 =_4 C_0x^4+_4 C_1x^3 +_4 C_2 x^2+_4 C_3 x+_4 C_4 1\end{aligned} \]
どうして二項係数が出てくるのか、またどうやってこの展開式を計算しているのでしょうか。
\((x+1)^2=(x+1)(x+1)\)の展開を考えると、2つの積において、\(x,x\)を選べば\(x^2\)が登場し、\(x,1\)を選べば\(x\)が登場し、\(1,1\)を選べが1が登場します。積の左側で\(x,1\)を選ぶので2通り、右側で\(x,1\)の2通り選ぶので、項をまとめなければ合計4通りの項があるわけです。ここで、\(x,1\)と\(1,x\)は同じ次数の項で、2通り分あるので、係数として2が出てきますね。2つの積から\(x\)を1つだけ選ぶので、\(_2 C_1 =2\)通りです。
\((x+1)^3 =(x+1)(x+1)(x+1)\)について考えてみましょう。それぞれ\(x^3\)の項、\(x^0=1\)の項は1通りしかありません。\(x^2\)の項は何通りあるでしょうか。\(3\)つの積から\(x\)を2つだけ選ぶのですから、\(_3 C_ 2 =3\)通りですね。
\(n=0,1,2,3\)の係数を、次のように並べて書いてみると、興味深い関係式が見つかります。

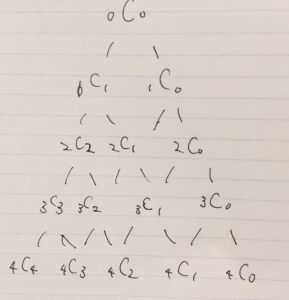
例えば\(n=2\)のところには\(1,2,1\)、\(n=3 \)のところには\(1,3,3,1\)という数が並んでいます。下の段に表れる数は、上につながった2つ(端なら1つ)の数の和になっています。つまり、\(_3 C_2 = _2 C_2 +_2C_1\)、\(_4 C_2 =_3 C_2 +_3 C _1\)といった関係性が成り立っています。
一般には、\(_{n+1}C_k = _n C_k +_n C_{k-1} \)が成り立ちます(これは組み合わせの表示式から証明できることです)。
つまり、この数の表は、例えば\(n=2\)のときの\(1,2,1\)から、足を2本伸ばしていって、その和によって\(n=3\)の\(1,3,3,1\)段を得る。といった手順の繰り返しによって、書くことができます。
この表がパスカルの三角形(Pascal’s triangle)と呼ばれるものです。一度自分で書いてみると、\(_{n}C_0 = _n C_n =1 \)や\(_n C_k = _n C _{n-k}\)、\(_{n+1}C_k = _n C_k +_n C_{k-1} \)といった式が馴染みやすくなるかと思います。
2つの項のべき乗を一般的に展開すると、
\[ \begin{aligned}(x+1)^n = _n C_n x^n+_n C_{n-1} x^{n-1}+\cdots +_n C_{1} x+ _n C_ 0 1 \\ = \sum_{k=0} ^n {}_n C_{n-k} x^{n-k}\\ =\sum_{k=0} ^n {}_n C_{k} x^{k}\end{aligned} \]
となりますね。これが二項定理と呼ばれるものです。
\((x+1)\)ではなく\((x+y)\)で考えれば、
\[ \begin{aligned}(x+y)^n = \sum_{k=0} ^n {}_n C_{k} x^{k}y^{n-k}\end{aligned} \]
となりますね。
二項定理の一般的な形だけ覚えようとすると、僕には難しかったです。まずは、\((x+1)^2,(x+1)^3,(x+1)^4\)を計算してみて、そこに登場する二項係数を考えると、一般的な形がどうなるか想像しやすいのではないでしょうか。
組み合わせの公式の覚え方
\(_n C _k\)の具体的な値はイメージしやすくなった一方で、結局
\[ \begin{aligned}_n C_ k = \frac{n!}{k!(n-k)!}\end{aligned} \]
をどう覚えたら良いでしょうか。
まず、機械的に覚えないことです。\(_n C_ k\)は、\(n\)個の対象から\(k\)個を取り出すときのパターンの個数という定義を意識しましょう。
\(n,k\)とか文字式で言うと難しいので、\(3\)個から\(2\)個取り出す、といった具体的なイメージを持ちます。例えば\(a,b,c\)という対象があったとしましょう(記号はなんでも良いです)。順番まで区別したときのパターン数(順列)は、\(ab,ba,bc,cb,ac,ca\)の6通りです(\(_3 P _2 =6\))。ところが\(ab,ba\)のような順序を区別しないのが組み合わせの数なので、全体を\(2\)で割って3通りとなります(\(_3 C_2 = \frac{_3 P_2 }{2}= 3\))。
少し数を増やして、\(5\)個から\(3\)個取り出すときはどうでしょうか。\(abc,acb,bac,bca,cab,cba\)、……と数えるとキリがありません。順列でいえば、最初の一文字に5通り、2文字目に4通り、3文字目に3通りなので、\(_5 P _3 = 5 \cdot 4 \cdot 3=60\)通りあります。しかし組み合わせとしてみれば同一視できるものがあり、\(abc\)グループは\(3\cdot 2\cdot 1= 3! =6\)通り分の重複があります。したがって、その重複を取り除けば\(_5 C_ 3= \frac{_5 P _3}{3!}= \frac{5\cdot 4\cdot 3}{3\cdot 2}=10\)通りとわかりました。
ここまでの考え方を一般化すると、\(n\)個のものから異なる\(k\)個を取り出して、順序を意識して並べると、\(_n P_k = n \cdot (n-1)\cdots (n-k+1)\)通りあります。そしてそれぞれのグループで重複しているのは、\(k!\)通りです。したがって、\(_n C_ k = \frac{_n P_k}{k!} =\frac{n (n-1)\cdots (n-k+1)}{k!}\)という式が得られました。
これを変形すれば、
\[ \begin{aligned}\frac{n (n-1)\cdots (n-k+1)}{k!} = \frac{n! }{k!(n-k)!}\end{aligned} \]
と求める公式が得られます。
やはり一般形で書くと難しくなりますね。
まずは\(_ 4 C_2\)といった式を見て、まず4個から2個を順番を考慮して並べれば\(4 \cdot 3\)通り、それぞれでの重複が\(2!\)通りなので、\(_4 C_2= \frac{4\cdot 3}{2!} =6\)と計算していくと良いでしょう。試しに\(_6 C_2 \)、\(_7 C_4\)を求めてみてください。分子は上から何個順に減っていく数の積を取って、分母は重複するパターンの数だけ取る。
掛け算九九を覚えるときも、書いたり読んだりしてだんだん覚えていったかと思います。それと同じで、\(n,k\)が\(1,2,3,4,5, \cdots\)といったときの計算をしてみてください。
それに慣れてきたら、一般形\(_n C_k = \frac{_n P_k}{k!} \)を思い出せるようにしてみましょう。分子は\(n (n-1)\cdots (n-k)\)と間違えやすいのですが、上から\(k\)個の積を取っています。\(n (n-1)\)が\(2\)個の積、\(n(n-1)(n-2)\)が\(3\)個の積である、…と考えていけば、\(n(n-1)\cdots (n-k+1)\)が\(k\)個の積であることがわかるでしょう。
\(_n C_k = \frac{_n P_k}{k!} \)という式を覚えることができれば、階乗の定義を使って整理すれば\(_n C_ k = \frac{n!}{k!(n-k)!}\)が得られます。ただし、具体的な計算を行う上では、\( \frac{_n P_k}{k!} \)の方が約分しやすくて使いやすいでしょう。
以上、組み合わせ・二項係数の覚え方として、パスカルの三角形や、組み合わせの考え方を紹介してきました。
組み合わせは確率を考えるときに役立ちますが、二項定理は多項式のテイラー展開にも役立つもので、\(_n C_k\)を理解することは長期的に価値あるものです。
具体的なケースで計算するのは少し面倒くさいかもしれませんが、手を動かしてみると、一般形\(\frac{_n P_k}{k!}\)も難なく受け止めるようになっていくと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。