どうも、木村(@kimu3_slime)です。
今回は、多項式補間とは何か、Juliaによる計算例を紹介します。
補間とは
ロボットの制御をしていて、指定された場所を通る動きをなめらかに実現したい、という問題を考えましょう。
一般に、\(n\)個の点(データ)\((x_1,y_1),\dots, (x_n,y_n)\)を通る連続的に定義された関数を見つける問題は、補間(interpolation)、内挿と呼ばれます。特に多項式関数を使った補間は、多項式補間(polynomial interpolation)、曲線あてはめ(curve fitting)と呼ばれるものです。
コンピュータを使った設計ソフトCADやイラストソフトでは、ベジエ曲線と呼ばれる指定された点を通るなめらかな曲線が描けますが、その基礎にあるのは補間の考え方です。

画像引用:Cubic_Bézier_Curve – Wikipedia, CC 表示-継承 4.0
補間のごく簡単な例を考えましょう。\((0,1),(1,3)\)という2点を通る1次関数\(y=ax+b\)を探してみましょう。2点の情報から\(b=1,a=2\)と求められるので、\(y= 2x+1\)が求める補間です。1次関数を使った直線的な補間は、線形補間と呼ばれます。
2次関数では3点、3次関数では3点、\(n\)次関数では\(n+1\)点のデータがあれば、それを通る多項式補間を求められます。一般に、\(n\)次多項式は異なる\(n+1\)点を通れば、ただ一つに決まるという数学的性質があるのです。これを決定するアルゴリズムとして、ラグランジュ補間(Lagrange interpolation)やニュートン補間(Newton interpolation)が知られています。
補間の考え方は、最小二乗法を使った線形回帰と少し似ています。線形回帰では点そのものは通らなくても良いが誤差を最小化するものを探し、補間では必ず指定された点を通るような関数を探しています。
準備
プログラミング言語Juliaを使って、補間の例を計算してみます。
Interpolations.jlを使うので、持っていなければインストールしておきましょう。
1 2 | using Pkg Pkg.add("Interpolations") |
準備として、以下のコードを実行しておきます。
1 | using Interpolations, Plots |
Juliaによる計算例
区間\([-3,3]\)において関数\(f(x)=e^{-x^2}\)を考え、\(x\)が整数となる点のデータを補間する多項式を求め、図示しててみましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | # Data Deinition a = -3 b = 3 x = a:1.0:b y = @. exp(-x^2) # Interpolations itp_const = ConstantInterpolation(x, y) itp_linear = LinearInterpolation(x, y) itp_cubic = CubicSplineInterpolation(x, y) # Interpolation functions f_const(x) = itp_const(x) f_linear(x) = itp_linear(x) f_cubic(x) = itp_cubic(x) # Plots x_new = a:0.1:b scatter(x, y, markersize=10,label="Data points") plot!(f_const, x_new, w=3,label="Constant interpolation") plot!(f_linear, x_new, w=3,label="Linear interpolation") plot!(f_cubic, x_new, linestyle=:dash, w=3, label="Cubic Spline interpolation") |
\(x,y\)としてデータを与え、「ConstantInterpolation」で定数補間、「LinearInterpolation」で線形補間、「CubicSplineInterpolation」で3次補間を計算しています。
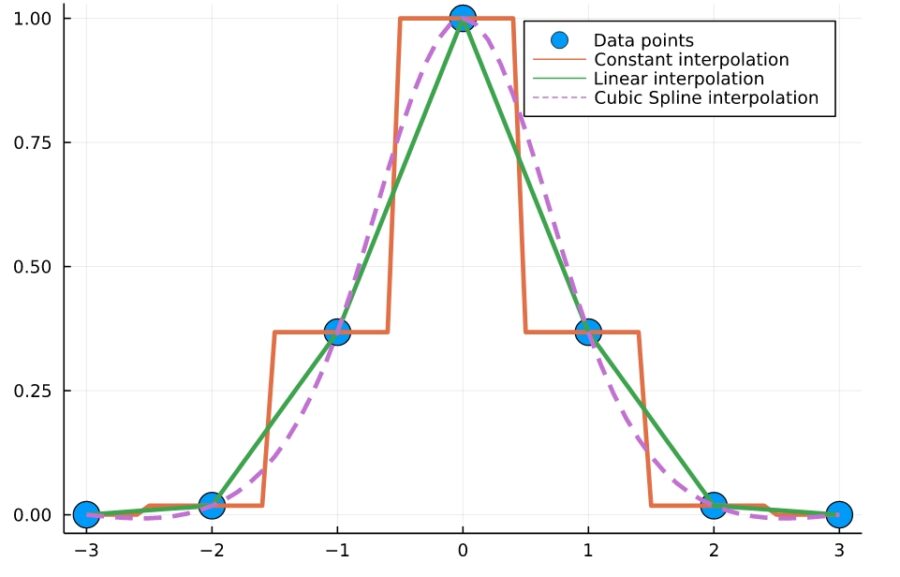
この方法は、それぞれの2点間における多項式補間を区分的に求めてつなぎあわせたもので、スプライン補間(spline interpolation)と呼ばれています。線形スプライン補間は、いわゆる折れ線近似ですね。次数が増えるほど、よりなめらかな曲線で近似できています。
データ数が多いときに全体をひとつの多項式で表すような大域的な補間をすると、手本としたい関数との誤差が大きくなってしまうケースが知られています(ルンゲ現象)。そこで区分的に多項式を求めて、それらつなぎあわせたスプライン補間を考えるわけです。
ベジエ曲線における多項式補間では、部分的になめらかさが崩れるスプライン補間ではなく、バーンスタイン多項式による補間が行われています。なめらかな関数は多項式の次数を上げることでいくらでも精度よく近似できるという、ワイエルシュトラスの近似定理による方法です。
以上、多項式補間とは何か、Juliaによる計算例を紹介してきました。
テイラー展開では微分できる関数(連続データ)の多項式による近似を考えますが、多項式補間ではごく少ないデータ(離散データ)を近似する多項式を考えます。
コンピュータにおける数値計算でも、数式を近似する離散的な点をサンプルとして取って、点の間の情報は多項式で補間する方法は便利です。
離散的なデータの近似を考えるとき、もっとも基本的な方法として補間の考え方を知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
最小二乗法とは:最小二乗解の求め方、正規方程式、射影による理解