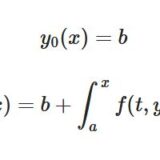稠密性とは：有理数、ワイエルシュトラスの近似定理を例に

どうも、木村（@kimu3_slime）です。

今回は、稠密性とは何か、有理数、ワイエルシュトラスの近似定理を例に紹介します。

有理数の稠密性
ワイエルシュトラスの近似定理
こちらもおすすめ

有理数の稠密性

稠密性（ちゅうみつせい）とは、基準となる空間\(X\)において、その部分集合\(D\)がみっちりと詰まっていることを表しています。いわゆる「密です」。

典型的な例として、実数\(\mathbb{R}\)において、有理数\(\mathbb{Q}\)という部分集合は稠密です。実数直線には、有理数点がバランスよくあらゆる場所に含まれています。

それは何を意味しているか。あらゆる実数\(x\)に対し、その近くに必ず有理数が存在するということです。\(\varepsilon >0\)を（十分小さな）実数として、開球\(B(x,\varepsilon)=\{y \in \mathbb{R} \mid |y-x|<\varepsilon \}\)を考えましょう。

十分大きな自然数\(m\)を取ることで、\(m\varepsilon >1\)とできます（アルキメデスの性質）。また、\(n-1 \leq mx <n \)を満たす整数\(n\)が存在します。これらを合わせれば、\(mx < n \leq mx+1<m(x+\varepsilon)\)です。\(m\)で割れば、\(x< \frac{n}{m}<x+\varepsilon\)で、\(\frac{n}{m} \in \mathbb{Q}\)が存在することがわかりました。

この事実を言い換えると、あらゆる実数\(x\)はある有理数列の極限として近似できる、ということです（例えば、各\(B(x,\frac{1}{\ell})\)から有理数を取っていけばいい）。ルートや円周率は小数で近似することができますが（実数の十進小数展開）、それを支えているのが実数における有理数の稠密性です。

一般に、位相空間\(X\)の部分集合\(D\)に対し、\(D\)を含む閉集合全体の共通部分を\(\mathrm{Cl}(D)\)と書き、\(D\)の閉包（closure）と呼びます。

そして、\(\mathrm{Cl}(D)=X\)が成り立つ時、\(D\)は\(X\)において稠密（dense）である、と定義します。

有理数の稠密性、\(\mathrm{Cl}(\mathbb{Q})=\mathbb{R}\)を示しましょう。\(\mathbb{R}\)はそれ自身が閉集合なので、閉包の定義から\(\mathrm{Cl}(\mathbb{Q})\subset \mathbb{R}\)は当然成り立ちます。\(\mathbb{Q}\)を含む閉集合は、\(\mathbb{R}\)以外にないことを、背理法により示しましょう。\(\mathbb{Q}\)を含む閉集合\(A\)で、\(\mathbb{R}\)に等しくないものが存在したとします。\(\mathbb{R} \backslash A\)は空でない開集合なので、そこから点\(x\)を選び、ある開球\(B(x,\varepsilon)\)を考えましょう。さきほど示したことから、そこには有理数が含まれます。これは\(\mathbb{R} \backslash A\)が有理数を含まないことに矛盾します。よって、有理数の稠密性が示せました。

\(D\)が\(X\)において稠密であることは、一般的に次のように言い換えられます。任意の空でない開集合\(U\)に対し、\(U \cap D \neq \varnothing\)が成り立つこと。\(X\)の各点\(x\)は、\(x\in D\)であるか、\(x\)の集積点（accumulation point）である（\(x\)を含む任意の開集合が、\(x\)以外の\(D\)の要素を含む）こと。

ワイエルシュトラスの近似定理

\(\mathbb{R}\)はすべての「数」を含んでいて便利な対象ですが、例えば無理数を扱うのは一般には難しいです。しかしそこには稠密な集合\(\mathbb{Q}\)があるので、一般の実数\(x\)を常にわかりやすい有理数で近似して扱うことができます。

このような考え方が、稠密性を考えるメリットです。とはいえ、有理数の例だけだとピンと来ないかもしれません。僕が学んだときは、稠密性が何の役に立つのか疑問に思いました。

そこで、関数空間における稠密性の例を紹介します。

ワイエルシュトラスの近似定理（Weierstrass approximation theorem）

\(f\)を有界閉区間\([a,b]\)上で定義された連続関数とする。任意の\(\varepsilon>0\)に対し、\(\mathrm{max}_{x \in [a,b]} |f(x)-p(x)| <\varepsilon\)を満たす多項式\(p\)が存在する。

\(C([a,b])\)を\([a,b]\)上の連続関数のなす空間、\(P([a,b])\)を\([a,b]\)上の多項式関数のなす空間とします。この近似定理は、\(P([a,b])\)が\(C([a,b])\)において稠密である、と主張するものです。どんな連続関数を考えても、常に多項式関数で（最大値ノルムの意味で）近似できる、というわけですね。

ワイエルシュトラスの近似定理は、有界閉区間だけでなく、一般にコンパクトな部分集合についても成り立つことが知られています。それはストーン・ワイエルシュトラスの定理と呼ばれるものです。

関数を多項式で近似するという点では、テイラー展開と似たものがあります。テイラー展開では（高次の）微分可能性が要求され、かつ収束半径という制約があります。ワイエルシュトラスによる多項式近似では、近似するためにただ連続であるだけで良いのが便利です。その分、多項式そのものが簡単な形にはならず、具体的に扱うのは難しくなります。

また、\(C_c^\infty(U) \)を、無限回微分可能な関数で、\(0\)でない値を取る部分がコンパクトである（コンパクトな台を持つ関数）の集合とします。\(L^p(U)\)を（ルベーグの意味で）\(p\)乗可積分な関数のなす空間とします（\(1\leq p <\infty\)）。このとき、\(L^p\)において\(C_c ^\infty\)は稠密であることが知られています。

積分可能な関数の形は一般には複雑ですが、それをなめらかな関数で常に近似できる、という便利な主張です。しかも、近似関数が\(0\)でない値を取る部分はコンパクトであるようになっています。

ジャンプや角のあるような関数\(f\)も\(L^p\)には含まれていますが、\(f\)をなめらかにしたような関数で近似できます。例えば微分方程式について、なめらかな関数について性質が成り立つことを示せたら、なめらかでない関数についても一般にその性質が成り立つ、といった議論ができます。これは軟化子（mollifier）の理論と呼ばれるものです。

ワイエルシュトラスの近似定理や、\(L^p\)における\(C_c ^\infty\)の稠密性について、詳しくは吉田「ルベーグ積分入門使うための理論と演習」や黒田「関数解析」を参照してみてください。

以上、稠密性とは何か、有理数、ワイエルシュトラスの近似定理などを例に紹介してきました。

一般的な対象（実数や関数）に関する性質を示すために、それをわかりやすい対象（有理数や連続関数）で近似できたらとても便利です。稠密性とは、都合の良い部分集合で近似したい、という考え方と言えるのではないでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。