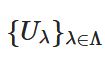連結性とは：実数区間、中間値の定理を例に

どうも、木村（@kimu3_slime）です。

今回は、連結な集合とはどういうものか、実数区間、中間値の定理を例に紹介します。

中間値の定理とは
連結性とは
連結性による証明
こちらもおすすめ

中間値の定理とは

中間値の定理とは、連続関数が中間の値をすべて取るという基本的な性質を表す定理です。

実数\(\mathbb{R}\)の閉区間\([a,b]:=\{x \mid a\leq x \leq b\}\)において定義された連続な関数\(f\)を考える。\(f(a) \leq f(b)\)とする。

すべての実数\(d\)、\(f(a) \leq d \leq f(b)\)に対して、\(f(c)= d\)を満たす実数\(c\)、\(c\in [a,b]\)が存在する。

例えば、\(I=[0,\frac{\pi}{2}]\)、\(f(x)=\sin x\)とすると、\(f(0)=0,f(\frac{\pi}{2})=1\)なので、\(\sin x\)は\(I\)において0以上1以下の値をすべて取ります。\(x=\frac{\pi}{6},\frac{\pi}{4}\)のような有名角における値は知られていますが、それ以外の値も\(0 \leq x \leq \frac{\pi}{2}\)のどこかで取っていることはわかるわけです。

中間値の定理は、\(f(x)=0\)を満たす\(x\)（零点、根、解）の存在を示すためにも使われます。ニュートン法は、その零点を見つける近似列を作る方法ですが、前提として中間値の定理があります。

中間値の定理は、実数の閉区間\([a,b]\)がひとまとまりにつながっている（連結である）ことに支えられています。

例えば、\(J=[0,1]\cup [2,3]\)、\(f(x)=x\)としましょう。\(f\)は\(J\)において連続です。\(f(0)=0\)、\(f(3)=3\)ですが、\(f\)は0以上3以下の値をすべて取るわけではありません。例えば、\(f(x)=\frac{3}{2}\)を満たす\(x\in J\)は存在しませんね。

中間値の定理が成り立つかどうかには、連続関数の定義域が連結かどうかがポイントなのです。（もちろん連続性もポイントですが）

連結性とは

\(J=[0,1]\cup [2,3]\)は、実数の連結でない集合の例です。いかにもつながっていない感じがしますが、それは共通部分を持たない2つの部分に分けられるからですね。

部分集合\(K\subset \mathbb{R}\)が連結でない（disconnected）とは、\(K \subset U\cup V\)、\(U \cap V \cap K= \varnothing\)、\(U \cap K \neq \varnothing\)、\(V \cap K \neq \varnothing\)を満たす実数の開集合\(U,V\)が存在することです。そのような開集合が存在しない時、\(K\)を連結である（connected）と呼びます。

ちょっと複雑になりましたが、言わんとしていることは難しくありません。まず一般に、実数の開区間\((a,b)\)は開集合となります。

\(J\)が連結でないことを示しましょう。\(U=(-0.1,1.1)\)、\(V=(1.9,3.1)\)とします。\(U,V\)は開区間なので、開集合です。そして、少し大きく取ったので\(J \subset U \cup V\)は成り立ちます。また、共通部分を持ちません\(U \cap V \cap K= \varnothing\)。そして、それぞれが空集合であるような無意味なケースとはなっていません\(U \cap J =[0,1] \neq \varnothing\)、\(V \cap J = [2,3] \neq \varnothing\)。

さらに一般には、実数の区間\((a,b),[a,b]\)や\(\mathbb{R}\)それ自身は、連結であることが知られています。それは実数の構成法、実数の連続性の公理によるものです。

今回は実数\(\mathbb{R}\)の部分集合を考えていますが、ユークリッド空間\(\mathbb{R}^N\)（や一般の位相空間）でも同様の定義をします。

\(\mathbb{R}^N\)の連結な開集合は、領域（domain）と呼ばれます。

例えば、\(U = \{(x,y)\mid x^2+y^2=1\}\)、\(V= \{(x,y) \mid (x-3)^2+y^2=1\}\)、\(W = U \cup V\)とすると、\(W\)は\(\mathbb{R}^2\)の領域ではありません。特に、連結ではありません。\(U,V\)は\(\mathbb{R}^2\)の開集合であり、\(W\)を2つの部分に分離しています。

連結性による証明

連結性という概念を導入すると、中間値の定理は見通し良く証明されます。

\(X\)を連結な集合とし、\(f:X \to Y\)を連続関数とします。すると、\(f\)の像\(f(X):=\{ y \in Y \mid \exists x \in X ,f(x)=y\}\)も連結となる。

これは位相空間における一般論として成り立つものです。

実数\(\mathbb{R}\)の閉区間\([a,b]\)において定義された連続な関数\(f\)を考え、\(f(a) \leq f(b)\)と仮定します。\([a,b]\)は連結ですから、\(f([a,b])\)も連結です。

中間値の定理の結論は、\( [f(a),f(b)] \subset f([a,b])\)となることと言い換えられます。これが成り立つことを示しましょう。

背理法によって示します。実数\(d\)で、\(f(a) \leq d \leq f(b)\)を満たし、\(d \not \in f([a,b])\)となるものが存在したとしましょう。\(d =f(a),d=f(b)\)のケースでは値を取るので、それ以外のケースとして\(f(a) < d < f(b)\)を考えます。

ここから、\(f([a,b])\)が連結でないことが示せてしまうのです。\(U=(-\infty, d)\)、\(V=(d,\infty)\)とすると、\(U,V\)は開集合です。\(d \not \in f([a,b])\)なので、\(f([a,b])\subset U \cup V\)です。\(U,V\)の取り方から、\(U \cap V \cap f([a,b])= \varnothing\)。\(f(a) \in U \cap f([a,b])\)と\(f(b) \in V \cap f([a,b])\)から、\(U\cap f([a,b])\neq \varnothing\)、\(V\cap f([a,b])\neq \varnothing\)で、\(f([a,b])\)は連結ではありません。これは矛盾です。

よって\( [f(a),f(b)] \subset f([a,b])\)が成り立ち、「すべての実数\(d\)、\(f(a) \leq d \leq f(b)\)に対して、\(f(c)= d\)を満たす実数\(c\)、\(c\in [a,b]\)が存在する」ことが示せました。

以上、連結性とはどういうものか、実数区間、中間値の定理を例に紹介してきました。

中間値の定理は微積分における基礎的な定理ですが、それは「連結集合の連続写像による像は連結」という一般論に支えられています。

当たり前に成り立っていそうなつながりに関する性質を、連結性・開集合といった一般的な枠組みを使って示せる部分には、位相空間論の一般性の魅力を感じますね。

木村すらいむ（@kimu3_slime）でした。ではでは。