どうも、木村(@kimu3_slime)です。
前回は、不等式を使って大小比較することによって、ルートの近似値を手計算で求めました。
今回は、精度の良い近似値を求める方法として、ニュートン法を紹介します。
ニュートン法とは
ニュートン法は、関数\(f\)の\(f(c)=0\)となる点\(c\)(\(f\)の零点)の近似列を、微分の情報を使って見つける方法です。ニュートン-ラフソン法(Newton-Raphson method)とも。
まず簡単な例として、\(f(x)=x^2-a\)に関するニュートン法を見てみましょう。
\(a=2\)のとき、\(f(c)=0,\quad c>0\)は\(c=\sqrt{2}\)を意味します。つまり\(\sqrt{2}\)の近似列を求めることができます。
\(f(x_1)>0\)となる\(x_1\)から出発して、\(x_1\)より\(c\)に近づく\(x_2\)を作ってみましょう。
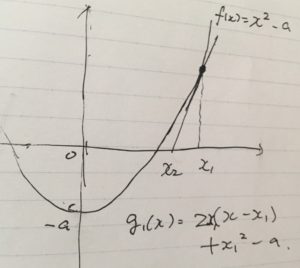
\(x=x_1\)における\(f\)の接線を\(g_1(x)\)とすると、傾きは\(2x_1\)で点\((x_1,x_1^2-a)\)を通る直線なので、\(g_1(x)=2x_1(x-x_1)+x_1^2 -a\)です。
\(f\)の2回微分は常に正\(f^{\prime \prime}(x)=2>0\)なので、\(f\)は(下に)凸関数であり、接線\(g_1\)は\(f\)の下側に来ます。
そこで\(g_1=0\)となる点を\(x_2\)としましょう。整理すれば、
\[ \begin{aligned}x_2 = x_1+\frac{1}{2x_1}(a-x_1^2)=\frac{1}{2}(x_1+\frac{a}{x_1})\end{aligned} \]
となります。さらに\(x_2\)を通る接線から\(x_3\)を構成し……と続けると、一般には
\[ \begin{aligned}x_{n+1} = x_n+\frac{1}{2x_n}(a-x_n^2)=\frac{1}{2}(x_n+\frac{a}{x_n})\end{aligned} \]
なる数列\(\{x_n\}_{n\in\mathbb{N}}\)が考えられます。この数列は単調減少であり、\(c\)に収束することが知られています。
ルート2の近似値を手計算と電卓で求める
\(a=2\)として、\(\sqrt{2}\)の近似値を手計算で求めてみましょう。
\[ \begin{aligned}x_{n+1} =\frac{1}{2}(x_n+\frac{2}{x_n})\end{aligned} \]
\(x_1=2\)として、\(x_2,x_3,x_4\)を計算します。
\[ \begin{aligned}x_2 =\frac{1}{2}(2+\frac{3}{2})=\frac{3}{2}=1.5\end{aligned} \]
\[ \begin{aligned}x_3=\frac{1}{2}(\frac{3}{2}+\frac{2}{\frac{3}{2}})=\frac{17}{12}\simeq 1.416666\cdots\end{aligned} \]
\[ \begin{aligned}x_4 =\frac{1}{2}(\frac{17}{12}+\frac{2}{\frac{17}{12}})=\frac{577}{408}\simeq 1.414215\cdots\end{aligned} \]
分数の計算は手計算で、最後の近似値を求める計算では電卓を使いました。
実際の値は\(\sqrt{2}\simeq 1.414213\cdots\)ですから、\(x_4\)の時点で小数点以下5桁まで一致していることがわかります。
大小比較による方法では、小数点以下2桁を求めるためにすら\(\sqrt{20000}\)を評価しなければならないので、ニュートン法の方がかなり楽だと感じますね。
ルートの近似値をプログラムで求める
ニュートン法をプログラミング言語Juliaで実行してみました(ウェブ上で実行結果が見れます)。降籏大介さんのページを参考にさせていただきました。
\(\sqrt{2}\)のニュートン法による近似の結果はこちら。\(n,x_n,f(x_n)\)の値が並んでいます。
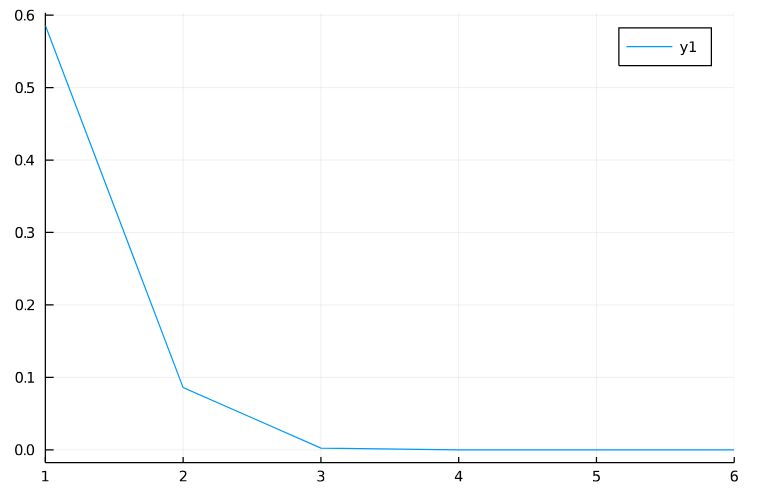
\(f(x_n)\)はどんどん小さくなり、ほぼ収束しました。
真の値(プログラミング言語における\(\sqrt{2}\))との差をグラフにすれば、次のようにグッと収束しているのがわかります。
\(\sqrt{5}\)の計算結果はこちら。
うまく収束し、少なくとも小数点以下15桁まで真の値と一致していることがわかります。
ニュートン法の一般形
ニュートン法は\(f(x)=x^2-a\)だけでなく、もう少し一般の形でも実行できます。
\(f\)を閉区間\([a,b]\)で2回微分可能で、常に\(f^{\prime\prime }(x)>0\)、端点で符号が変化している\(f(a)f(b)<0\)としましょう。
このとき、\(a,b\)の間に\(f(c)=0\)となる点が存在します(中間値の定理)。\(f(x_1)>0\)なる点\(x_1\)から出発し、さきほど見てきたような点列を構成しましょう。
\(x_n\)における接線の方程式は、\(g_n(x)=f^{\prime}(x_n)(x-x_n) +f(x_n)\)です。\(g_n=0\)となる点を\(x_{n+1}\)とすれば、
\[ \begin{aligned}x_{n+1}= x_n -\frac{f(x_n)}{f^{\prime}(x_n)}\end{aligned} \]
という点列が得られます。
\(f\)が凸関数\(f^{\prime\prime }(x)>0\)であることから、\(f\)の区間内における零点は唯一つであること、\(f^{\prime}(x_n)\neq 0\)であること、点列\(\{x_n\}_{n\in \mathbb{N}}\)は有界な単調列であり、零点に収束することが示せます。詳しくは、杉浦「解析入門 Ⅰ」pp.105-106を参照してください。
仮定は常に\(f^{\prime\prime }(x)<0\)でも大丈夫です(\(-f\)を考えれば良い)。
円周率\(\pi\)の近似値も、ニュートン法を使って求められます。
\(f(x)=\sin x -\frac{1}{2}\)を使って、\(x=\frac{\pi}{6}\)の近似をコンピュータで計算します。\(x_1=0.5\)とすると、\(f^{\prime\prime} (x) <0\)で、\(f(x_1)<0\)なので、(\(-f\)に対して)ニュートン法が適応できます。
1 2 3 4 | 1 0.5 -0.020574461395796995 2 0.523444473818484 -0.0001336352128983309 3 0.5235987687270579 -5.95066923514409e-9 4 0.5235987755982988 -5.551115123125783e-17 |
\(6x_4=3.141592653589793\)で、\(\pi\)を小数点以下16桁まで近似できていることがわかりました。
(\(f(x)=\sin x\)として\(x=2\pi\)の近似列を作ってみましたが、\(f^{\prime\prime} (2\pi) =0\)でありながら、問題なく\(2\pi\)の近似値\(6.283185307179586\)が得られました。おそらく、区間内で\(f^{\prime}(x)\)が0にならないという弱い仮定で、ニュートン法はうまくいくのではないでしょうか。参考:お話:数値解析 第10回非線型方程式(前編))
同様の方法で、\(\log_e x-1\)の零点として、オイラー数\(x=e\)の近似値が求められますね。
以上、平方根を求めるためのニュートン法、\(\sqrt{2},\sqrt{3},\sqrt{5}\)のプログラミング計算、一般的なニュートン法とその計算を紹介してきました。
\(f(x)=0\)は一般に非線形方程式と呼ばれますが、ニュートン法は非線形方程式の数値解法を与えてくれています。\(f\)が多項式の場合、例えば\(5\)次以上多項式による方程式には一般的な解の公式がないことが知られていますが、そうであっても数値解が求められるわけです。
もし無理数の値や、非線形方程式の零点を求めたいけれども、理論的にきれいに解けないときは、ニュートン法という手法を思い出してみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080
こちらもおすすめ
なぜe(オイラー数)を学ぶ? 指数関数、対数関数の微分を単純化