微積分学(calculus)・解析学(analysis)は、線形代数学と並び、大学で数学をする人はもちろん、自然科学や工学、社会科学や人文科学を学ぶすべての人が身につけて損はない数学(教養数学)です。高校数学では、微分と積分の初歩的な内容を学びます。
物理を代表とした科学全般で、微分方程式をモデルとした数学が応用されていますが、その分析には微積分学が必須です。さらに、フーリエ解析と偏微分方程式や複素解析といった分野の基礎でもあるのが、微積分学です。ちなみに、僕の学生時代の専門は偏微分方程式です。
この記事では、大学1-2年で学ぶ微積分に関する記事を分野ごとにまとめて紹介します。特に重要なキーワードは
- 微分、積分、微積分学の基本定理、極限
- テイラー展開、近似、オーダー
- 逆三角関数、双曲線関数
- 広義積分、ガウス積分、ガンマ関数
- 多変数関数、ベクトル値関数、ベクトル場
- 偏微分、勾配、接平面
- ヤコビ行列、ヘッセ行列
- 合成関数の微分(チェインルール)
- 重積分、線積分、面積分
- 回転、発散
- グリーンの定理、ガウスの発散定理、ストークスの定理
- 級数の比較判定法、収束半径、一様収束
です。知らないものがあれば、優先して学ぶと良いでしょう。
微積分学の初歩、応用
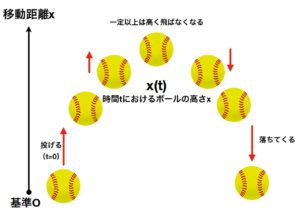
微積分学の基本概念は、微分と積分です。
微分は、関数の瞬間的な変化を取り出す割り算です。幾何学的にはグラフの接線を求めることで、物理的には速度や加速度の概念につながります。
積分は、関数の値を連続的に足し合わせる足し算です。幾何学的にはグラフの面積を求めることで、物理的には移動距離や仕事の概念につながります。
微分と積分は全く別の概念ですが、それらを結びつける重要な定理が、微積分学の基本定理です。これがあるので、微分と積分はセットで微積分学として学ばれています。
微分と積分の基礎には、限りなく近づく値:極限の考え方があります。
中学高校大学で数学、微積分を学ぶ理由・応用のひとつは、数理モデルとしての微分方程式にあると僕は考えています。
なぜe(オイラー数)を学ぶ? 指数関数、対数関数の微分を単純化
商f/gの微分公式の覚え方:合成関数・積の微分による導出・証明
1変数の微分:近似、テイラー展開
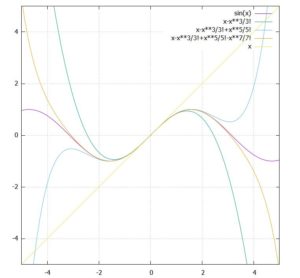
微積分について、高校数学では扱わず、大学独自の内容として最初に身に着けたいのが、テイラー展開の考え方です。高校数学では、微分係数を使ってグラフの接線を求める方法を学びました。接線とは1次関数のことですが、2次関数や3次関数といった多項式関数で近似することについて学びます。
有名な極限の公式f(x)/xの覚え方:接線近似とテイラー展開
三角・指数・対数関数と多項式の不等式:テイラー展開に関連して
常用対数の頻出値log_10(2),log_10(3)を、テイラー展開で求めてみよう
連続関数、可積分関数の線形空間(関数空間)、微分と積分の線形性とは
初等関数
高校で学ぶ多項式関数、三角関数、指数関数・対数関数、三角関数は、微積分学において重要です。これらの和、積、合成、逆関数は、初等関数と呼ばれます。
高校で扱わない初等関数としては、逆三角関数、双曲線関数が重要です。
1変数の積分:広義積分
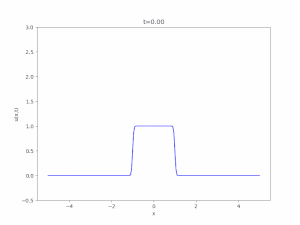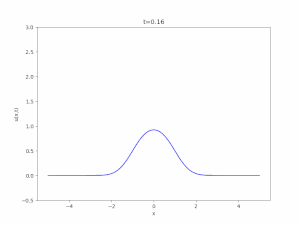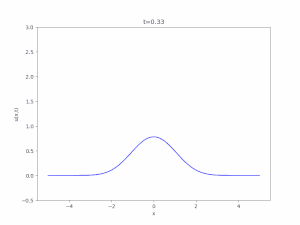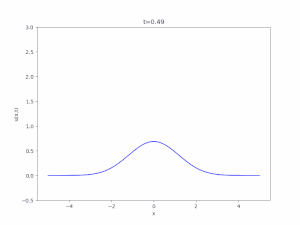
高校数学では、主に有限の区間における連続な関数の積分を扱います。無限の大きさを持った区間や、区間の端で連続でない関数に対しても積分が定義でき、それは広義積分と呼ばれます。広義積分の例として、統計学や偏微分方程式にも登場するガウス積分や、階乗の一般化であるガンマ関数は重要です。
sinc関数とは? 正弦積分の近似値をテイラー展開で求めてみよう
多変数の微分
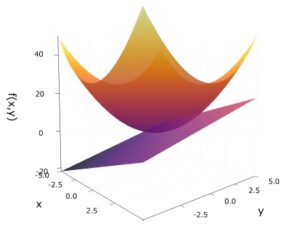
高校数学では、1変数の実数値関数の微分や積分について学びました。大学では、多変数のベクトル値関数の微積分について学びます。これはベクトル解析とも呼ばれる分野です。
ひとつの変数に注目した微分が、偏微分です。偏微分係数を並べたベクトルは勾配と呼ばれ、グラフの接平面に関係します。
2変数関数も、1変数関数と同様にテイラー展開することができます。1変数関数の最大値最小値の判定に2階導関数が重要だったのと同じように、2変数関数の最大値最小値はヘッセ行列が重要です。
1変数のベクトル値関数は曲線、多変数のベクトル値関数はベクトル場として解釈することができます。
勾配ベクトルが等位曲面に垂直である(法線ベクトル):例と証明
ベクトル値関数をベクトル場として描いてみよう:ヤコビ行列と線形近似
逆二乗力(重力場、電磁場)のポテンシャルがラプラス方程式を満たすことの証明
多変数の積分
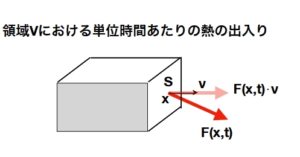
熱や水の空間的な増減を調べるには、多変数の積分:重積分、面積分、線積分が必要になります。
微積分の基本定理の拡張として、グリーンの定理、ガウスの発散定理、ストークスの定理が重要です。これらにはベクトル場の回転、発散という考え方が関わってきます。
級数と極限、収束
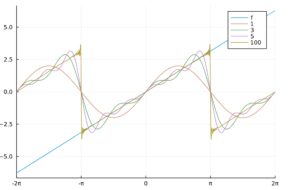
テイラー展開、関数を別のわかりやすい関数の足し合わせ=級数として捉えるには、極限や収束に対する考え方を深める必要があります。テイラー展開は局所的な近似であり、一般的には有効な範囲:収束半径の概念があります。
テイラー展開は多項式関数による近似を考えますが、三角関数による近似をする方法もあり、それはフーリエ解析と呼ばれています。
微分と級数の順序交換、積分と級数の順序交換といった、極限の順序交換の正当化は重要な問題ですが、それには一様収束の考え方が役立ちます。
lim 1/n=0はなぜ? ε-n_0論法とアルキメデスの性質
微積分の基礎、実数論、位相
しばしば、学部1年の最初から次に示すような基礎的な内容が教えられることがありますが、難しいので僕個人としてはおすすめしません。上で述べてきたような応用を一通り身につけた上で、数学的な基礎を学びたい人はチャレンジしましょう。
微積分学の基礎である極限の考え方を一般的に行うには、イプシロンデルタ論法と呼ばれる議論が有効です。
また、微積分の基礎的な定理として、最大値の定理や中間値の定理がありますが、これらの基礎を掘り下げていくと、実数の公理に突き当たります。特に、上限・下限、有界性といった考え方は広く応用されるものです。
関数の定義域の性質(開区間か閉区間か)によって、関数の性質(例えば最大値を持つか)は変わりますが、それを一般化していくとユークリッド空間の位相、位相空間論につながる理解が得られます。
連続関数とは:イプシロンデルタと開集合、閉集合による特徴づけ
上限・下限(sup,inf)、有界とは:具体例、最大・最小値との違い
部分列、ボルツァーノ・ワイエルシュトラスの定理とは:点列コンパクトとの関係
数列の上極限・下極限(limsup,liminf)の例、性質
関数の連続(極限)と数列連続(点列連続)の定義が同値であることの証明
各点連続、一様連続、リプシッツ連続の違い:イプシロンデルタ論法を具体的に
コンピュータ
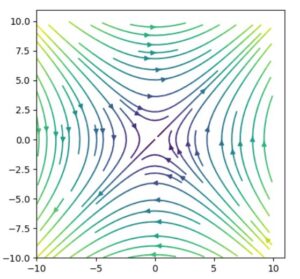
多変数関数のグラフや、ベクトル場を手描きで可視化するのは大変です。コンピュータを使うと簡単に描けて、その考え方が直観的に理解しやすくなるでしょう。
Juliaで1変数関数のグラフを描く方法(多項式、指数対数、三角関数)
Julia(SymPy)で1変数関数を微分する方法(多項式、指数対数、三角関数)
Julia(SymPy)で1変数関数を積分する方法(多項式、指数対数、三角関数)
Julia(SymPy)で1変数関数の最大値最小値を求める方法
Julia(SymPy)で三角関数の加法定理、倍角の公式、和積の公式、合成を求める方法
Julia(SymPy)で数列の和、無限級数、べき級数を求める方法
Julia(Plotly)でグリグリ動かせる3Dグラフを作る方法
Julia(SymPy)で偏微分、勾配、発散、回転、合成関数の微分を計算する方法
Julia(Optim)で2変数関数の最小値・最大値を求める方法
Julia(PyPlot)で2次元のベクトル場・流線を描く方法
Julia(SymPy)でパラメータ付けられた曲線(平面、空間)を描く方法
Julia(Plots)でパラメータ付けられた曲面を描く方法
Julia(Plots)で二次曲線(円、楕円、双曲線)を陰関数として描く方法
Julia(SymPy)でスカラー場・ベクトル場の線積分を計算する方法
Julia(SymPy)で実数区間の開集合、閉集合、内部、閉包、境界、有界性を判定する方法
教科書
やさしい順に並べています。
詳しくは:大学入学前に数学を予習したい人におすすめの本・勉強
マセマ出版社 (2017-03-19T00:00:01Z)
¥3,680
マセマ出版社 (2020-02-05T00:00:01Z)
¥4,686 (コレクター商品)
共立出版 (1984-12-21T00:00:01Z)
¥4,840 (コレクター商品)
岩波書店 (1978-03-23T00:00:01Z)
¥3,980 (コレクター商品)
岩波書店 (1981-11-15T00:00:01Z)
¥5,500
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740