無限回微分可能であるがテイラー展開できない例について

どうも、木村（@kimu3_slime）です。

今回は、無限回微分可能であるが、テイラー展開できない関数の例を紹介します。

無限回微分可能、テイラー展開とは

関数\(f: I \to \mathbb{R}\)が\(x=a\)で無限回微分可能である（infinitely differentiable）とは、任意の自然数\(n \in \mathbb{N}\)に対して、\(n\)回微分可能であることです。つまり、何回でも微分できることを意味しています。区間\(I\)の各点で無限可能であるとき、\(I\)上で無限可能微分可能と呼びます。

例えば、多項式、三角関数、指数関数は\(\mathbb{R}\)上で、対数関数は\((0,\infty)\)上で無限回微分可能です。

\(k\)回微分可能である関数のなす空間は\(C^k\)、無限回微分可能である関数のなす空間は\(C^\infty\)と表されます。

参考：連続関数、可積分関数の線形空間（関数空間）、微分と積分の線形性とは

\(f\)を区間\(I\)上で\(n+1\)回微分可能な関数とするとき、任意の\(a,x \in I\)に対して

\[ \begin{aligned}f(x)=f(a)+f'(a)(x-a)+ \cdots + \\ \frac{f^{(n)}(a)}{n!}(x-a)^n + R_{n+1}(x)\end{aligned} \]

\[ \begin{aligned}R_{n+1}(x)=\frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1}\end{aligned} \]

を満たす\(a<c<x\)が存在します。これをテイラーの定理というのでした。

参考：テイラー展開の展開式の覚え方、導き方、証明

\(f\)が\(I\)上で無限回微分可能であるとき、もし剰余項が消えていく

\[ \begin{aligned}\lim _{n\to \infty}R_{n+1}(x) =0\end{aligned} \]

ならば、

\[ \begin{aligned}f(x) = \sum_{k=0}^\infty \frac{f^{(k)}(a)}{k!}(x-a)^k\end{aligned} \]

という無限級数として表せます。この等式が成り立つとき、\(f\)は\(x=a\)を中心として\(I\)上でテイラー展開可能、べき級数展開可能と呼びましょう。

例えば、三角関数、指数関数は\(\mathbb{R}\)上テイラー展開可能です。また、対数関数\(\log(1+x)\)は\(x=0\)を中心として\((-1,1)\)上でテイラー展開可能です。

参考：べき級数の収束半径とは何か、テイラー展開を例にした求め方

関数\(f\)が無限回微分可能ならば、

\[ \begin{aligned}\sum_{k=0}^\infty \frac{f^{(k)}(a)}{k!}(x-a)^k\end{aligned} \]

というテイラー級数が定まります。しかし、それはいつでも\(f\)に一致するとは限らない、テイラー展開可能でない例があることを紹介しましょう。

\[ \begin{aligned}f(x)= \begin{cases}0 & (x \leq 0 )\\e^{-\frac{1}{x}} & (x>0)\end{cases}\end{aligned} \]

という関数を考えます。

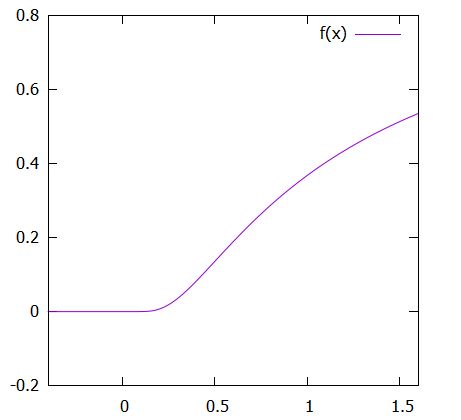
この関数は、\(x=0\)を含む開区間で無限回微分可能です。\(x<0\)では定数関数なので良いでしょう。\(x>0\)のときも、\(e^{-\frac{1}{x}}\)は無限回微分可能な関数同士の合成関数なので、無限回微分可能です。

微妙なのは、\(x=0\)での微分可能性です。これは微分の定義によって直接確かめられます。左側極限は、

\[ \begin{aligned}\lim_{h\nearrow 0}\frac{f(h)-f(0)}{h}=\lim_ {h\nearrow 0}\frac{0-0}{h}= 0\end{aligned} \]

です。右側極限は、\(y = \frac{1}{h}\)と置くと\(h \to 0\)のとき\(y \to \infty\)なので、

\[ \begin{aligned} \lim_{h\searrow 0}\frac{f(h)-f(0)}{h}&=\lim_ {h\searrow 0}\frac{e^{-\frac{1}{h}}}{h}\\ &=\lim_ {y\to \infty} \frac{y}{e^y}\\ &=0 \end{aligned} \]

です。どんな多項式よりも指数関数は速く発散するので。

参考：三角・指数・対数関数と多項式の不等式：テイラー展開に関連して

よって、右側極限と左側極限が一致するので、\(f\)は\(x=0\)で微分可能で、\(f^{\prime}(0)=0\)です。

さらに、無限回微分可能であることが示せます。\(x>0\)のときの導関数は\(f^{\prime}(x) = \frac{1}{x^2}e^{-\frac{1}{x}}= \frac{1}{x^2} f(x)\)です。

\[ \begin{aligned} f^{\prime \prime}(x)&=-\frac{2}{x^3}f(x)+\frac{1}{x^2}f^{\prime}(x) \\ &= \frac{1-2x}{x^4}f(x) \end{aligned} \]

一般には、

\[ \begin{aligned} f^{(n)}(x)&= \frac{p_n(x)}{x^{2n}}f(x) \end{aligned} \]

\(p_n\)は\(n-1\)次以下の多項式と表せます。数学的帰納法で示しましょう。\(n=1\)のときは既に示しました。\(n=k\)のとき正しいと仮定すると、

\[ \begin{aligned} f^{(k+1)}(x)&= (\frac{p_k(x)}{x^{2k}})^{\prime}f(x) +\frac{p_k(x)}{x^{2k}} f^{\prime}(x) \\&= \frac{p_k ^\prime (x) x^{2k}-p_k(x) 2k x^{2k-1}}{x^{4k}}f(x) +\frac{p_k(x)}{x^{2(k+1)}} f(x) \\ &= \frac{p_k^\prime(x) x^2+(1-2kx)p_k(x) }{x^{2(k+1)}}f(x)\end{aligned} \]

となり、分子は\(k\)次以下の多項式であることが示せました。よって、\(n+1\)回微分を定義する右側極限は

\[ \begin{aligned} \lim_{h\searrow 0}\frac{f^{(n)}(h)-f^{(n)}(0)}{h}&=\lim_ {h\searrow 0}\frac{\frac{p_n(h)}{h^{2n}} e^{-\frac{1}{h}}}{h}\\ &=\lim_ {y\to \infty} \frac{p_n(\frac{1}{y})y^{2n+1}}{e^y}\\ &=0 \end{aligned} \]

となります。分子は整理すれば\(n\)次以上の多項式が残り、多項式と指数関数の発散速度に比較から0となるので。

よって、\(f\)は\(x=0\)において無限回微分可能で、その導関数は\(f^{(n)}=0\)であると言えました。

一方で、\(f\)は\(x=0\)を含むどんな開区間\(I\)でも\(x=0\)を中心としてテイラー展開可能ではありません。\(x=0\)を中心としたテイラー級数は

\[ \begin{aligned} g(x)&:= \sum_{k=0}^\infty \frac{f^{(k)}(0)}{k!}x^k\\ \\ &= 0\end{aligned} \]

と恒等的に0になります。しかし、元の関数の\(x>0\)の部分を考えると、

\[ \begin{aligned}f(x)=e^{-\frac{1}{x}} \neq 0\end{aligned} \]

です。よって、\(f(x) \neq g(x)\)なる点\(x\in I\)が存在することになり、区間\(I\)でテイラー展開可能でないと言えました。

\(x>0\)の範囲で考えれば、テイラー展開が\(g(x)=0\)ということは、剰余項が常に\(R_{n+1}(x)=e^{-\frac{1}{x}} \)ということです。これは\(n \to \infty\)としても\(0\)に収束しませんね。

区間\(I\)でテイラー展開可能な関数を、実解析的（real analytic）であると呼びます。

解析的関数のなす空間は、しばしば\(C^{\omega}\)と表されます。\(\omega\)は最小の無限順序数を表す記号で、自然数の濃度、可算濃度\(\aleph_0\)のことです。級数はひとつの数列として表されることから、こうした記号を使うのでしょう。

参考：無限集合の濃度とは？写像の全単射、可算無限、カントールの対角線論法

今回紹介したのは、無限回微分可能・\(C^\infty\)級であるが、実解析的・\(C^\omega\)級ではない例です。何回でも微分できればテイラー展開できそうな気がするかもしれませんが、実際は剰余項がうまく消えてくれないような例もある、というわけですね。