どうも、木村(@kimu3_slime)です。
高校数学において、「極限は代入で求められる」と説明されるのをたまに目にします。それが限定的にしか正しくないことを、うまくいかない例を交えて紹介します。
連続ならば代入で求められる
極限値\(\lim _{x \to 1} (x^2-1) \)を求めよ、という問題を考えましょう。その値は、\(\lim _{x \to 1} x^2-1 = 1^2 -1 =0\)と求められます。
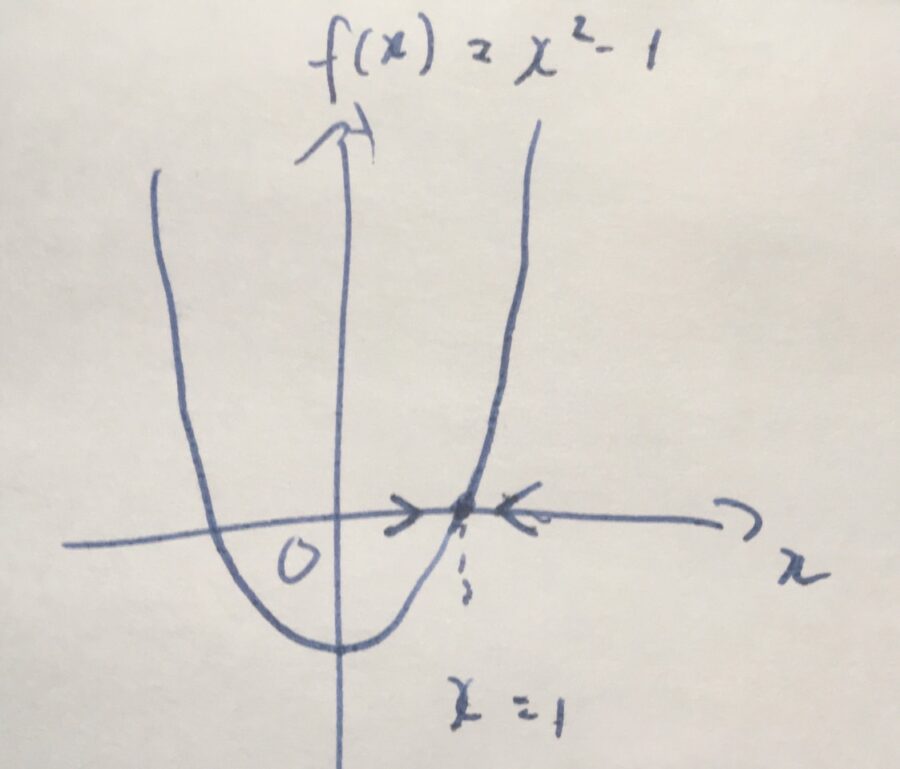
この例を見ると、極限値は代入によって求められる、と思ってしまいそうです。
一般論としては、もし関数\(f(x)\)が\(x= a\)において連続ならば、\(\lim_{x \to a}f(x) =f(a)\)が成り立ちます。つまり、連続な関数についてのみ、代入が成り立つのです。そもそも、このような代入が成り立つことが、連続性の定義です。
各点での連続性の定義
関数\(f(x)\)が\(x= a\)において連続とは、\(\lim_{x \to a}f(x) =f(a)\)が成り立つこと
区間での連続性の定義
関数\(f(x)\)が実数の区間\(I\)において連続とは、すべての\(a \in I\)について\(\lim_{x \to a}f(x) =f(a)\)が成り立つこと
高校数学では、\(x^2 -1\)のような多項式関数は、明らかに(実数全体で)連続な関数として扱われます。どの点を考えても、各点で連続な関数です。したがって、代入して議論して良い、とされるわけですね。
参考:各点連続、一様連続、リプシッツ連続の違い:イプシロンデルタ論法を具体的に
代入で求められない例
極限を考える意義は、むしろ単なる代入ができないような例を考えることにあります。
\(\lim_{x\to 1} \frac{x^2-1}{x-1}\)という例を考えましょう。
\(f(x) = \frac{x^2 -1}{x-1}\)は、何も断りがない限りは、\(x=1\)では定義されていないものとして考えるでしょう。\(x=1\)をそのまま代入すると、分母が\(0\)となるので(0割り算は定義されない)。

しかし、\(x=1\)で定義されていないとしても、\(x=1\)の付近で定義されている関数ならば、極限値を考えることができます。変数\(x \)が、\(x \neq 1\)という条件を満たしながら、\(1\)に近づくとき、\(f(x)\)はどんな値に近づくでしょうか。
\(x \neq 1\)という仮定があるので、分母分子を\(x-1\)で割ることはできて、\(f(x) = \frac{(x+1)(x-1)}{x-1}= x+1\)となります。
したがって、\(x+1\)が連続であることを利用すれば、\(\lim _{x \to 1} \frac{x^2-1}{x-1} = \lim_{x\to 1} (x+1)= 1+1 =2\)と求めることができました。
今回考えた\(f\)は、\(x=1\)で定義されていないので、連続性を使った「そのまま代入」の議論が使えないわけです。
もしこの未定義な値を\(f(1) =2\)と定義すれば、\(f\)は連続で、\(\lim_{x\to 1}f(x) =f(1)\)が成り立ちます。\(2\)以外の値、例えば\(f(1)=1\)と定義すれば、\(f\)は連続ではなく、\(\lim_{x \to 1}f(x) =f(1)\)は成り立ちません。
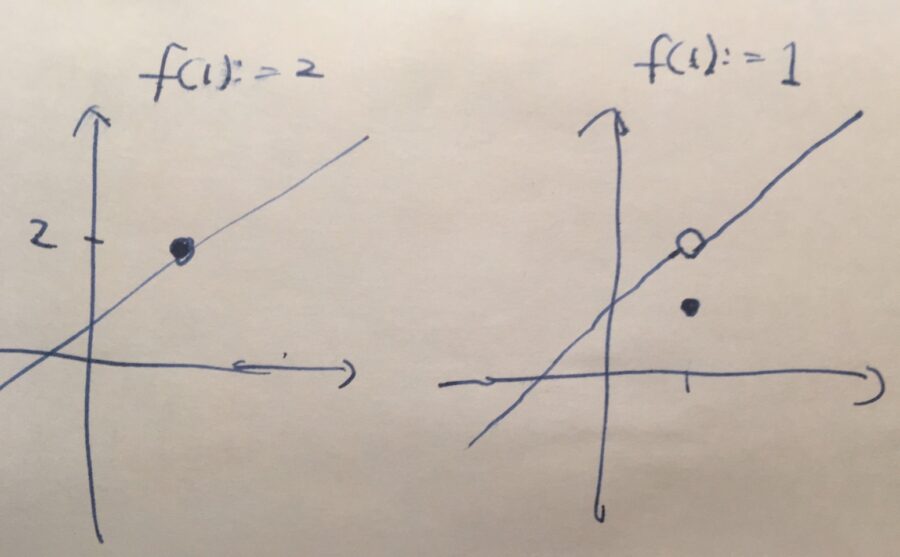
この例では、\(x=1\)に右側(正の方向)から近づけるときの極限値と、左側から(負の方向)から近づけるときの極限値が一致していました。一般には、それらが異なるケースもあります。
例えば、\(g(x) = \frac{1}{x}\)について考えましょう。この関数は、\(x=0\)で未定義です。しかし、\(x= 0\)に近づけるときの極限を考えることはできます。
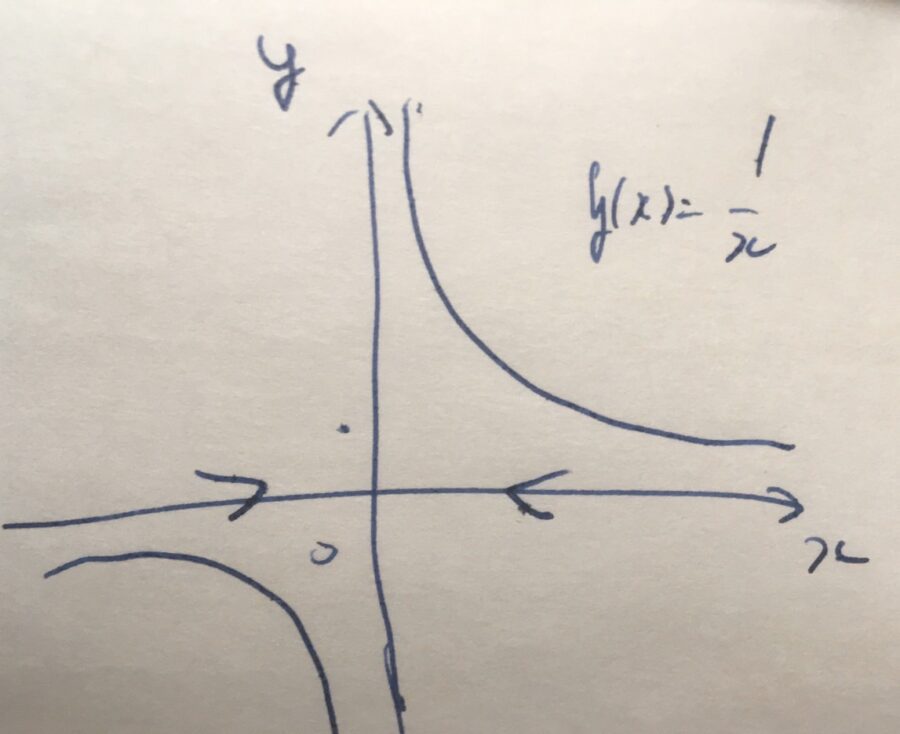
\(x>0\)を満たしたまま\(x \)を\(0\)に近づけると、\(\frac{1}{x}\)は限りなく大きな値を取ります。したがって、\(\lim_{x\searrow 1} \frac{1}{x}= \infty\)です。
一方、\(x<0\)を満たしたまま\(x \)を\(0\)に近づけると、\(\frac{1}{x}\)は限りなく負の方向に大きな値を取ります。したがって、\(\lim_{x\nearrow 1} \frac{1}{x}= -\infty\)です。
右側極限と左側極限が異なるので、この関数の\(x= 0\)での極限値は存在しません。
これは、\(\frac{1}{x}\)に\(x=0\)が「代入できない」とは意味が違います。単純に代入できないような関数でも、考える点付近で関数が近づいていく値については考察することができて、それが極限の考え方なのです。
例えば、\(\frac{1}{x}\)において\(x= \infty\)を「代入」することはできません(\(f(\infty)\)はそのままでは定義されていない)。しかし、\(x\)を大きくすればするほど、\(\frac{1}{x}\)はどんどん\(0\)に近づきます。その状況は\(\lim_{x \to \infty}\frac{1}{x} =0\)と表現できるわけです。
以上、極限値が代入で求められる条件について、うまくいかない例を交えて何が起こっているか考えてきました。
中学高校で扱う関数の多く、1次関数や2次関数などの多項式関数、指数関数や三角関数は連続関数です。これらについては、そのまま代入で極限を求めることができます。
しかし、それらを分数として組み合わせた有理関数は、連続であるとは限らず、単なる代入によって考察できなくなります。また、\(x= \infty\)のような未定義の値に関する考察にも、極限の考え方は役立ちます。
関数が連続かどうか、どの点で未定義になっているかを考えることで、「極限は単なる代入」という考え方を乗り越えましょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1978-03-23T00:00:01Z)
¥3,980 (コレクター商品)



