逆二乗力（重力場、電磁場）のポテンシャルがラプラス方程式を満たすことの証明

どうも、木村（@kimu3_slime）です。

今回は、逆二乗力（重力場、電磁場）のポテンシャルがラプラス方程式を満たすことについて紹介します。

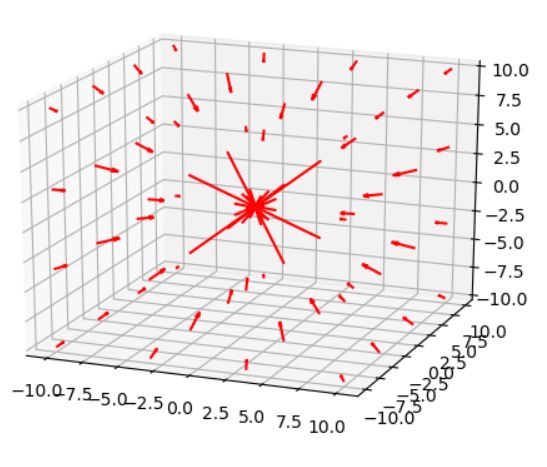
3次元空間\(\mathbb{R}^3\)において、2つの（点）質量や電荷がある状況を考えましょう。一方が原点にあるとき、もう一方の点\((x,y,z)\)に働く力（力場、ベクトル場）は、

\[ \begin{aligned}F(x,y,z)= – \frac{c}{r^3}(x,y,z)\end{aligned} \]

\[ \begin{aligned}r= \sqrt{x^2+y^2+z^2}\end{aligned} \]

と表されます（逆二乗則）。1次元の問題ならば、\(x=r\)で、\(-\frac{c}{r^3}x =-\frac{c}{r^2}\)と逆二乗の形になります。

これは重力ならば万有引力の法則、電磁気力ならばクーロンの法則を表したものです。係数、定数は一般的に\(c\)と表しました。\(c>0\)ならば引力、\(c<0\)ならば反発力（斥力）です。

ポテンシャルとは、ベクトル場の線積分、その微分がベクトル場となるような関数のことです。例えば、位置エネルギーは、ポテンシャルの一種です。

参考：力学的エネルギー保存の法則を、微積分で導出・証明する

一般に、\(F\)をベクトル値関数とするとき、勾配が\(\nabla f = F\)を満たす関数\(f\)を\(F\)のポテンシャル関数（potential function）と呼びます。ポテンシャル関数が存在するとき、\(F\)による仕事（線積分）は経路によらず端点のみで決まり、そのとき\(F\)は保存力（conservative force）であると呼ばれます。

参考：グリーンの定理の例による理解と証明、応用

さきほど紹介した逆二乗力の力場では、ポテンシャル関数が

\[ \begin{aligned}f(x,y,z)= \frac{c}{r}\end{aligned} \]

となり、さらにその勾配の勾配、すなわちラプラシアンが0

\[ \begin{aligned}\Delta f=0\end{aligned} \]

\[ \begin{aligned}\Delta f : = \frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2} +\frac{\partial^2 f}{\partial z^2}\end{aligned} \]

となること、ポテンシャルはラプラス方程式の解であることが知られています。

ラプラス方程式の解は調和関数、調和関数を調べる分野はポテンシャル論と呼ばれています。ポテンシャルの背後には、ラプラス方程式という偏微分方程式があるわけです。

これらを確かめてみましょう。

\(f = \frac{c}{r}\)がポテンシャル関数であるとは、勾配が\(\nabla f =F\)を満たすことでした。各偏微分を計算すると、合成関数の微分法則から

\[ \begin{aligned}\frac{\partial f}{\partial x}\\=c\frac{-1}{2}\frac{1}{(x^2+y^2+z^2)^{\frac{3}{2}}} 2x\\ =-c\frac{x}{r^3}\end{aligned} \]

となります。\(u=x^2+y^2+z^2\)と見ると、\(\frac{1}{u^{\frac{1}{2}}}=-\frac{1}{2}\frac{1}{u^{\frac{3}{2}}}\)で、\(\frac{\partial u}{\partial x}=2x\)であるので。同様に、

\[ \begin{aligned}\frac{\partial f}{\partial y}= -c\frac{y}{r^3}\end{aligned} \]

\[ \begin{aligned}\frac{\partial f}{\partial z}= -c\frac{z}{r^3}\end{aligned} \]

となるので、\(\nabla f =(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})=F\)が示せました。

さらに、2回偏微分を計算していきます。すると、合成関数の微分法則と商の微分法則

\[ \begin{aligned}(\frac{f(x)}{g(x)})^\prime = \frac{f^{\prime}(x)g(x) -f(x)g^\prime (x)}{(g (x))^2}\end{aligned} \]

から、\(\frac{\partial r}{\partial x}= \frac{2x}{2r}\)に気をつけて、

\[ \begin{aligned}\frac{\partial^2 f}{\partial x^2}\\=-c\frac{\partial }{\partial x}(\frac{x}{r^3}) \\ =-c\frac{1\cdot r^3 – x \cdot 3 r^2 \cdot \frac{2x}{2r}}{r^6}\\ =-c\frac{r^3-3rx^2}{r^6}\end{aligned} \]

となります。同様に、

\[ \begin{aligned}\frac{\partial^2 f}{\partial y^2} =-c\frac{r^3-3ry^2}{r^6}\end{aligned} \]

\[ \begin{aligned}\frac{\partial^2 f}{\partial z^2} =-c\frac{r^3-3rz^2}{r^6}\end{aligned} \]

です。よって、

\[ \begin{aligned}\Delta f \\ = -c(\frac{r^3-3rx^2}{r^6}+\frac{r^3-3ry^2}{r^6}+\frac{r^3-3rz^2}{r^6})\\ =-c\frac{3r^3 -3r(x^2+y^2+z^2)}{r^6} \\ =-c\frac{3r^3 -3r^3}{r^6}\\ =0 \end{aligned} \]

となることがわかりました。

以上、逆二乗力（重力場、電磁場）のポテンシャルがラプラス方程式を満たすことの証明を紹介してきました。

ポテンシャル論の入り口として、偏微分の計算だけで理解できる話なので、ぜひ逆二乗力の計算を試してみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。