どうも、木村(@kimu3_slime)です。
今回は、方向微分、法線微分の定義、例、求め方を紹介します。
方向微分とは
方向微分とは、端的に言えば偏微分の一般化です。
多変数の実数値関数\(f:\mathbb{R}^N \to \mathbb{R}\)について考えましょう。簡単のため、平面\(N=2\)のときを題材とします。
\(f\)の偏微分は、
\[ \begin{aligned}\frac{\partial f}{\partial x}(x,y):=\lim_{h\to 0}\frac{f(x+h,y)-f(x,y)}{h}\end{aligned} \]
\[ \begin{aligned}\frac{\partial f}{\partial y}(x,y):=\lim_{h\to 0}\frac{f(x,y+h)-f(x,y)}{h}\end{aligned} \]
といったように定義されました。それぞれ、第一成分の変化、第二成分の変化に注目した微分です。
これは軸に沿った方向の微分を考えていますが、もっと一般に\(a \in \mathbb{R}^N\)に沿った方向の微分を考えてみましょう。変数を\(x=(x_1,\dots,x_N)\)とベクトルでまとめて書くことにします。
\[ \begin{aligned}D_a f (x):=\lim_{h\to 0}\frac{f(x+ha)-f(x)}{h} \end{aligned} \]
という極限が存在するとき、方向微分可能と呼び、\(D_a f(x)\)を\(x\)における\(a\)方向の方向微分(directional derivative)・導関数と呼びます。偏微分の表記に合わせ、\(\frac{\partial f}{\partial a}(x)\)や\(\nabla _a f(x)\)と書くことも。
\(N=2,e_1=(1,0)\)のときは、
\[ \begin{aligned} D_{e_1} f (x)&=\lim_{h\to 0}\frac{f((x,y)+h(1,0))-f(x,y)}{h}\\&= \lim_{h\to 0}\frac{f(x+h,y)-f(x,y)}{h}\\&=\frac{\partial f}{\partial x}(x,y)\end{aligned} \]
となり、第一成分に関する偏微分に一致します。第二成分に関する偏微分は、\(e_2\)方向の方向微分と言えます。方向微分は偏微分の一般化、偏微分とは特殊な方向微分だった、というわけですね。
特に、1変数関数に関する通常の微分は、\(e_1=1\)という大きさ1でプラスの方向への微分です。
\(f(x)=x^2\)を例に、負の方向で大きさが1でない方向微分、\(a=-2\)とした方向微分を考えると、
\[ \begin{aligned} D_{-2}f(x)&=\lim _{h\to 0}\frac{f(x-2h)-f(x)}{h} \\ &= \lim _{h\to 0}\frac{x^2-4xh+4h^2-x^2}{h}\\ &= -4x \\&= a f^{\prime}(x)\end{aligned} \]
という関係になっています。
この関係は、次のように一般化されます。\(f\)の勾配を
\[ \begin{aligned}\nabla f:=\mathrm{grad} f:=Df\\:=(\frac{\partial f}{\partial x_1},\dots,\frac{\partial f}{\partial x_N})\end{aligned} \]
と表すとき、
\[ \begin{aligned}D_a f(x)= \langle Df(x) ,a\rangle\end{aligned} \]
が成り立ちます。右辺はベクトルのユークリッド内積です。この式は、\(f\)が各方向に連続微分可能(\(C^1\)級)のとき成り立ちます。
つまり、方向微分は、先に各方向の偏微分を計算して、それと方向\(a\)との内積を取ることで計算できます。
やってみましょう。\(f(x,y)=x^2+y^2\)の\((a,b)\)における方向微分を求めてみます。
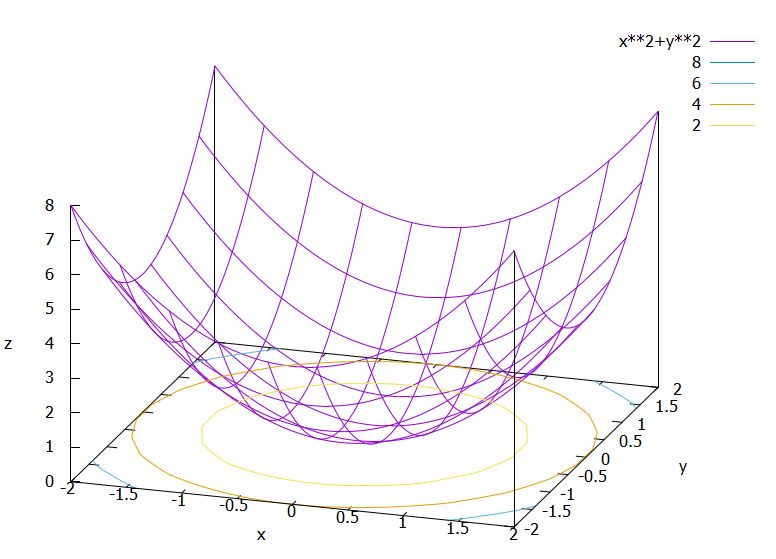
\(Df(x,y)=(2x,2y)\)なので、\(D_{(a,b)} f(x,y) =\langle Df,a\rangle=2ax+2by\)です。\((x,y)=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\)、\((a,b)=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\)のケースを考えると、\(D_{(a,b)} f(x,y)=2\)です。
円\(x^2+y^2=1\)上の点に注目して、軸からすれば斜めの点で斜めの方向の微分を測ってみると、\(\frac{\partial f}{\partial x}(1,0)=2\)や\(\frac{\partial f}{\partial y}(0,1)=2\)と、変化率が一致していることがわかりますね。
法線微分とは
方向微分の応用としてあるのが、法線微分です。
なめらかな曲線や曲面を考えると、各点でその接線や接平面に直交するベクトル、法線ベクトルが定まります。その法線ベクトル\(n\)に関する関数の方向微分
\[ \begin{aligned}\frac{\partial f}{\partial n }(x):= D_n f(x)=\langle Df(x) ,n\rangle\end{aligned} \]
を\(f\)の法線微分(normal derivative)と呼びます。法線ベクトルとしては、外向きの単位法線ベクトルを考えることが多いです。
\(x^2+y^2 =1\)という円における\(f(x,y)=x^2+y^2\)の法線微分を求めてみましょう。
円上の各点\((x,y)\)において、その外向き単位法線ベクトルは\(n=(x,y)\)です。
なぜなら、\(p(\theta)=(\cos \theta, \sin \theta)\)とパラメータ表示すると、接線上の点(接ベクトル)は\(p^{\prime}(\theta) = (-\sin \theta, \cos \theta)=(-y,x)\)であり、これは\(n\)と直交しています。
また、\(x^2+y^2=1\)なので、大きさは\(\|n\|= \sqrt{x^2+y^2}=1\)となっていますね。したがって、
\[ \begin{aligned} \frac{\partial f}{\partial n }(x,y)&= \langle(2x,2y) ,(x,y)\rangle \\ &= 2x^2+2y^2 \\&=2\end{aligned} \]
と一定であることがわかりました。どの点についても、外側への変化率が一定、というわけです。
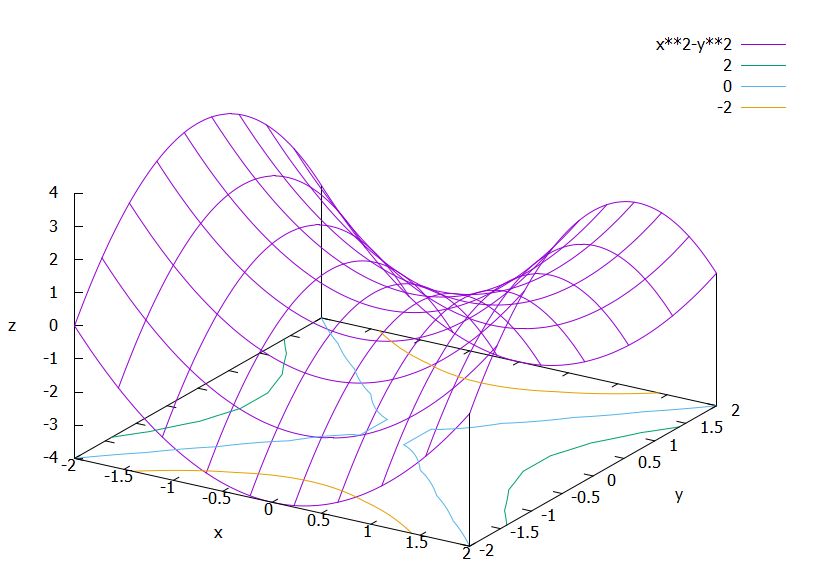
別の例として、\(f(x,y)=x^2-y^2\)の単位円における法線微分を計算すると、
\[ \begin{aligned} \frac{\partial f}{\partial n }(x,y)&= \langle(2x,-2y) ,(x,y)\rangle \\ &= 2x^2-2y^2 \end{aligned} \]
となり、位置によって変化率が異なることがわかりますね。
法線微分とガウスの発散定理
\[ \begin{aligned}\int_S \langle F,n\rangle = \int_D (\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}) dxdydz\end{aligned} \]
を組み合わせてみましょう。\(F= Df\)という関係があるとき(\(F\)が\(f\)の勾配ベクトル場であるとき)、左辺は法線微分の面積分ですね。したがって、
\[ \begin{aligned} \int_S \frac{\partial f}{\partial n} &= \int_D (\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}+\frac{\partial^2 f}{\partial z^2}) dxdydz\\ &= \int _D \Delta f dxdydz\end{aligned} \]
という式が成り立ちます。これはグリーンの公式やグリーンの恒等式と呼ばれるものです。
関数\(u\)に関する偏微分方程式において、考えている有界領域\(U\subset \mathbb{R}^N\)の境界条件として
\[ \begin{aligned}\frac{\partial f}{\partial n }(x) =g(x)\end{aligned} \]
と法線微分を指定する問題を考えることがあります。これはノイマン境界条件(Neumann boundary condition)、第二種境界条件と呼ばれるものです。
例えば、熱方程式において\(g=0\)のノイマン境界条件を考えるということは、境界では熱が変化しない、熱の出入りがない、つまり断熱条件を考えることに相当しています。
以上、方向微分、法線微分の定義、例、求め方を紹介してきました。
低い次元\(N=1,2,3\)で具体的に計算してみれば、そのイメージや意味はつかめると思うので、試してみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版 (1984-12-21T00:00:01Z)
¥682 (中古品)
岩波書店 (1978-03-23T00:00:01Z)
¥5,060
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080
東京大学出版会 (1985-04-25T00:00:01Z)
¥1,884 (中古品)







