閉集合、触点、閉包、集積点、孤立点とは：定義、性質、例

どうも、木村（@kimu3_slime）です。

今回は、閉集合、触点、閉包、集積点、孤立点といった概念の定義や性質について、ユークリッド空間での例を交えて紹介します。

閉集合、触点、閉包とは
集積点、孤立点とは
まとめ
こちらもおすすめ

閉集合、触点、閉包とは

ユークリッド空間\(\mathbb{R}^N\)（一般に距離空間）における議論をしていきましょう。今回紹介する概念は、数列や点列の収束と関係するものです。

例えば、\((a,b)\subset \mathbb{R}\)という開区間は、そのすべての点が外にはみ出ない近傍を持っています（すべての点が内点である）。このような集合を一般に開集合と呼ぶのでした。

一方で、\([a,b]\subset \mathbb{R}\)のように、端点（境界点）をすべて含むような集合を、閉集合と呼びます。\(A \subset \mathbb{R}^N\)が閉集合であることの定義のひとつは、その補集合\(\mathbb{R}^N \setminus A\)が開集合であることです。

閉集合は「その補集合が開集合」という捉え方とは、別の捉え方ができます。それが閉包という考え方です。

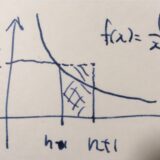
開区間\((0,1)\)や半開区間\([0,1)\)は閉集合でなく、閉区間\([0,1]\)は閉集合であることが示せます。これらの違いは何でしょうか。それは端っこの点、タッチしている点が含まれているかどうかですね。

例えば、\(A=(0,1)\)において、\(0 \in U\)であるものの、それはギリギリ接触していそうな点です。\((\frac{1}{n})_{n\in \mathbb{N}}\)という数列（点列）を考えれば、すべての\(n\)に対して\(\frac{1}{n} \in U\)であり（\(A\)の点列）、かつその極限は\(\lim_{n\to \infty} \frac{1}{n}=0\)となっています。

距離空間において、\(a \in \mathbb{R}^N\)が\(A\)の触点（adherent point, closure point, contact point）であるとは、\(A\)の点列\((a_n)_{n \in \mathbb{N}}\)で\(\lim_{n\to \infty} a_n=a\)を満たすものが存在することです。

上の例で見たように、\(0\)は\((0,1)\)の触点です。\(1\)や\(\frac{1}{2}\)も触点ですね。\(1.1\)は触点ではありません。

\(A\)を実数の部分集合として、実数\(K\)が\(A\)の上限であることは、\(K\)が\(A\)の上界かつ触点であることと同値であると知られています。

参考：数列と上限・下限の関係：有界な単調数列は収束する

（位相空間においては、\(a\in X\)が\(A \subset X\)の触点であるとは、\(a\)の任意の開近傍\(U\)に対し\(A \cap U \neq \varnothing\)と定義されます。これらは距離空間のケースでは同値な定義です。）

\(A\)の触点全体の集合を、\(A\)の閉包（closure）と呼び、\(\mathrm{Cl}(A)\)や\(\overline{A}\)と書きます。

\(A\)に属するすべての点は触点なので、\(A \subset \mathrm{Cl}(A)\)が常に成り立ちます。

（一般の位相空間においては、\(A\)を含むすべての閉集合の共通部分を閉包と呼びます。これは距離空間において上の定義と同値です。閉包は、\(A\)を含む最小の閉集合となります。）

例えば、\(\mathrm{Cl}((0,1))=[0,1]\)、\(\mathrm{Cl}([0,1))=[0,1]\)、\(\mathrm{Cl}([0,1])=[0,1]\)です。こうして見比べてみると、\(A\)が閉集合であるケースは\(A= \mathrm{Cl}(A)\)と一致して、閉集合でないときは\(A \neq \mathrm{Cl}(A)\)が成り立っていますね。

実際、\(A\)が閉集合であることと、閉包と等しくなること\(A= \mathrm{Cl}(A)\)は同値です。なぜか。

\(A\)を閉集合と仮定し、\(\mathrm{Cl}(A) \subset A\)を示しましょう。\(a \in \mathrm{Cl}(A)\)とします。触点の定義から、\(A\)の点列\((a_n)_{n \in \mathbb{N}}\)で\(\lim_{n\to \infty} a_n=a\)を満たすものを選びましょう。背理法によって示します。\(a \not \in A\)と仮定すると、\(\mathbb{R}^N \setminus A\)が開集合であることから、開球が\(B(a,\varepsilon) \subset \mathbb{R}^N \setminus A\)となる\(\varepsilon >0\)が存在します。一方で、点列の収束の定義から、「\(n \geq N\)ならば\(d(a,a_n) <\varepsilon\)」を満たす\(N\in \mathbb{N}\)が存在します。\(d(a,a_n) <\varepsilon\)とは、\(a_n \in B(a, \varepsilon)\)を満たすことですが、そこから\(a_n \not \in A\)となってしまい、それが\(A\)の点列であることに矛盾しました。よって、\(a \in A\)です。

一方で逆を示すために、対偶：\(A\)が閉集合でないならば、\(A \neq \mathrm{Cl}(A)\)を示しましょう。仮定から\(\mathbb{R}^N\setminus A\)が開集合でないので、ある点\(a \in \mathbb{R}^N\setminus A \)で「任意の\(\varepsilon >0\)に対し、\(B(a,\varepsilon) \not \subset \mathbb{R}^N\setminus A\)」を満たすものが存在します。\(a \not \in A\)が触点であることを示しましょう。\(\varepsilon = \frac{1}{n}\)として、\(a_n \in B(a, \frac{1}{n}),a_n \not\in \mathbb{R}^N\setminus A\)を満たす\(a_n \)が存在します。\(a_n \in A\)なので、\((a_n)\)は\(A\)の点列です。また、\(d(a,a_n)= \frac{1}{n} \)より、\(\lim_{n\to \infty}a_n =a\)です。よって、\(A \neq \mathrm{Cl}(A)\)が示せました。

また、閉包と等しくなること\(A= \mathrm{Cl}(A)\)は、\(A\)が点列について閉じていること（任意の\(A\)の点列は、収束するならばその極限は\(A\)に属する）と同値です。

\(A= \mathrm{Cl}(A)\)と仮定し、収束する\(A\)の点列\(\lim_{n\to \infty}a_n =a\)を考えましょう。これは\(A\)の点列なので、\(a\)は\(A\)の触点です。したがって、仮定から\(a \in A= \mathrm{Cl}(A)\)が言えました。

一方、\(A\)が点列について閉じていると仮定します。\(a \in \mathrm{Cl}(A)\)を任意の点としましょう。触点の定義から、\(A\)の点列\((a_n)_{n \in \mathbb{N}}\)で\(\lim_{n\to \infty} a_n=a\)を満たすものが存在します。仮定より、\(a \in A\)です。したがって、\(A= \mathrm{Cl}(A)\)が示せました。

さらに、\(A\)が閉集合であることは、境界点をすべて含む\(\mathrm{Fr}(A) \subset A\)と同値です。

\(A\)を閉集合と仮定し、\(a \in \mathrm{Fr}(A)\)とします。境界点の定義から、\(a\)に収束する\(A\)の点列が作れます。\(A\)は点列について閉じていることから、\(a \in A\)であるとわかりました。

一方で\(\mathrm{Fr}(A) \subset A\)と仮定します。\(\mathbb{R}^N \setminus A\)が開集合であることを示しましょう。\(a \in \mathbb{R}^N \setminus A\)とすると、仮定より\(a \not \in \mathrm{Fr}(A)\)です。境界点でないことの定義から、「\(B(a,\varepsilon) \cap A=\varnothing\)または\(B(a,\varepsilon) \cap (\mathbb{R}^N \setminus A)=\varnothing\)」を満たす\(\varepsilon\)が存在します。\(a \in \mathbb{R}^N \setminus A\)より、後者は成り立ちません。したがって、\(B(a,\varepsilon) \cap A=\varnothing\)となり、\(B(a,\varepsilon) \subset (\mathbb{R}^N \setminus A)\)が導かれます。つまり\(a\)は\(\mathbb{R}^N \setminus A\)の内点で、結論が言えました。

（一般に、境界は閉包と内部の差に等しい\(\mathrm{Fr}(A)= \mathrm{Cl}(A)\setminus \mathrm{Int}(A)\)ことが示せます）

集積点、孤立点とは

このように触点は点列の極限に関する概念ですが、もう少し別の見方があります。

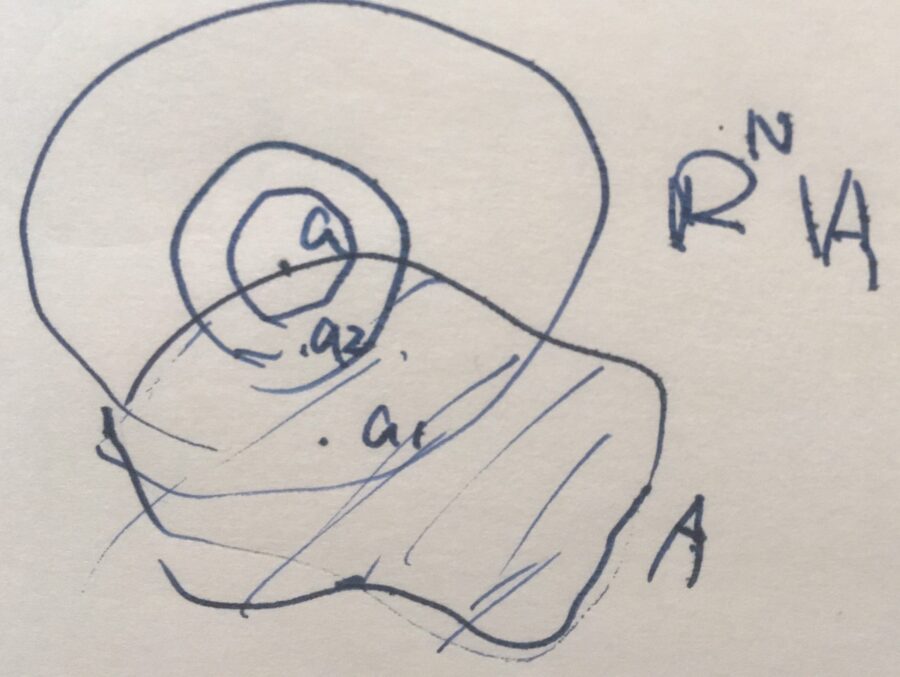
\(a \in \mathbb{R}^N\)が\(A \)の集積点（accumulation point）・極限点（limit point）であるとは、\(a\in \mathrm{Cl}(A \setminus\{a\})\)を満たすことです。\(a \in A\)であって、かつ集積点でないとき、それは\(A\)の孤立点（isolated point）と呼ばれます。

例として、\(A=(0,1)\cup \{2\}\)を考えましょう。\(0,1\)は集積点ですが、\(2\)は集積点ではありません。\(2\)自身を使わずに、\(2\)に収束するような\(A\)の点列は作れませんね。\(A\setminus \{2\}=(0,1)\)なので、\((0,1)\)の点列は必ず\(d(a_n,2) \geq 1\)を満たしてしまいます。

集積点は、自明な点列\(a_n=a\)以外の点列によって近似できる点のことです。\(2 \in A\)なので、\(2\)は孤立点です。まさに1点だけポツンと浮いていますが、そのイメージを正確に述べれば集積点ではないということです。

すべての集積点は、触点でもあります。なぜなら、\(\mathrm{Cl}(A \setminus\{a\}) \subset \mathrm{Cl}(A)\)なので。

また、\(a\not \in A\)のときは、\(a\)が集積点であることと触点であることは同値です。\(A\setminus \{a\}= A\)となるので、\(\mathrm{Cl}(A\setminus\{a\})= \mathrm{Cl}(A)\)。ただし、\(a \in A\)のときは、触点であるが集積点でない例が存在します。さきほどの例で見たように、孤立点があるケースです。

まとめると、触点は集積点か孤立点、いずれか一方に分類されます。\(a \not \in A\)のときは触点＝集積点、\(a \in A\)のときは触点＝集積点または孤立点です。

（位相空間においては、\(a\)が\(A\)の集積点であることは、\(a\)の任意の開近傍\(U\)に対し、\((U\setminus\{a\}) \cap A \neq \varnothing\)と同値です。）