Julia（PyPlot）で2次元のベクトル場・流線を描く方法

どうも、木村（@kimu3_slime）です。

今回は、Julia（PyPlot）で2次元のベクトル場・流線を描く方法を作る方法を紹介します。

この記事のコードと実行結果（GitHub）

準備

PyPlotを使うので、持っていなければインストールしておきましょう。

グラフを描く準備として、以下のコードを実行します。

2次元のベクトル場を描く方法

例として、いくつかの2変数のベクトル値関数（平面のベクトル場）の図（流線）を描いてみましょう。

線形ベクトル場を

\[ \begin{aligned}F(x,y)= \begin{pmatrix} a&b\\c&d \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} ax+by\\cx+dy \end{pmatrix}\end{aligned} \]

と表します。

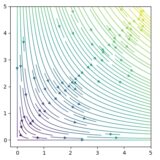
\(F(x,y)=(x,y)\)、つまり\(a=1,b=0,c=0,d=1\)のとき、次のコードで描くことができます。

「range」は描写する範囲の指定です。\(x,y\)ともに-5から5まで、sampleの数（200）だけ分割して値を取ることにします。

「u = a*x+b*y, v = c*x+d*y」が、ベクトル場の定義式です。

「PyPlot.streamplot(x, y, u, v)」によって、結果を図として出力します。各点でのベクトル場の大きさ（速度）に応じて色を変えるために、「speed」を計算し、「color=speed」で割り当てています。「density」で線の密度を調整できます。

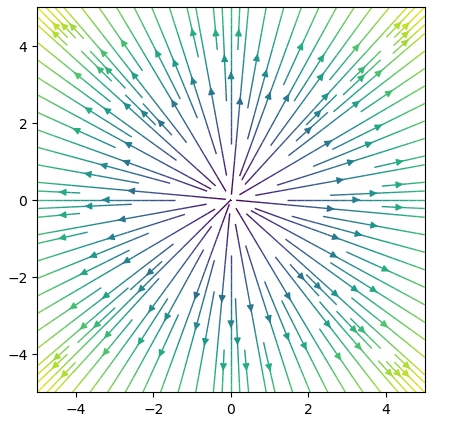
係数を変えて、同様の方法で描いてみましょう。

\[ \begin{aligned}F(x,y)=(-x,-y)\end{aligned} \]

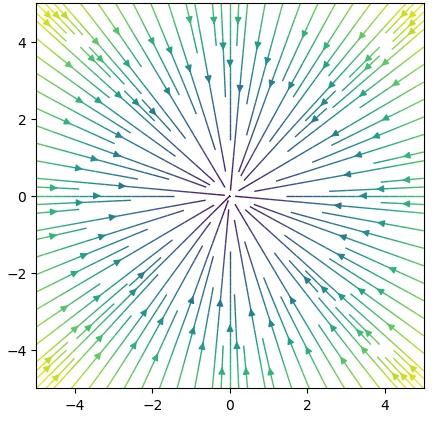
\[ \begin{aligned}F(x,y)=\begin{pmatrix} 0&1\\1&0 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} y\\x \end{pmatrix}\end{aligned} \]

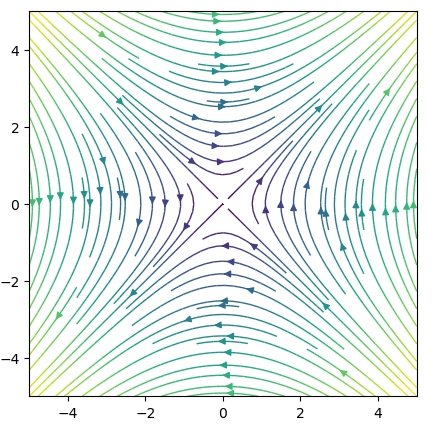
\[ \begin{aligned}F(x,y)=\begin{pmatrix} 0&1\\-1&0 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} y\\-x \end{pmatrix}\end{aligned} \]

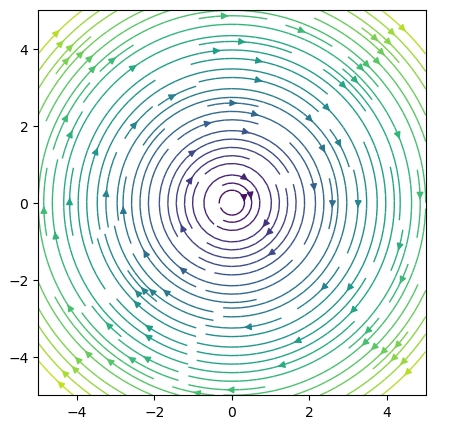
\[ \begin{aligned}F(x,y)=\begin{pmatrix} -1&1\\-1&-1 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} -x+y\\-x-y \end{pmatrix}\end{aligned} \]

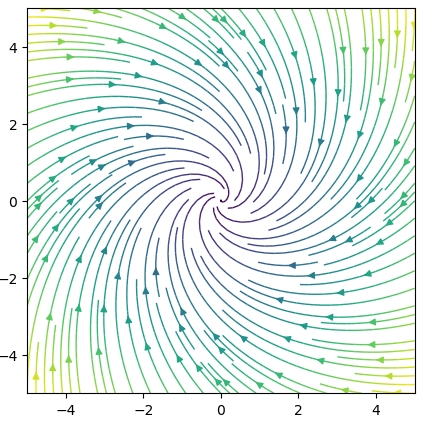
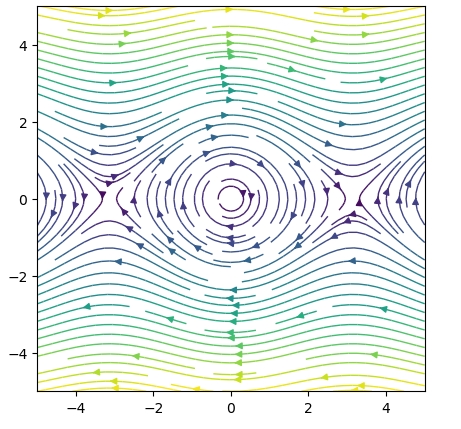
\(F(x,y)=(y,-\sin x)\)という非線形のベクトル場を描きましょう。

ベクトル場の定義式を、「sin.(x)」に置き換えるだけです。配列に対する計算なので、ドットをつけるのを忘れないようにしましょう。

最後に、矢印（quiver）を使ってベクトル場を描く方法を紹介します。

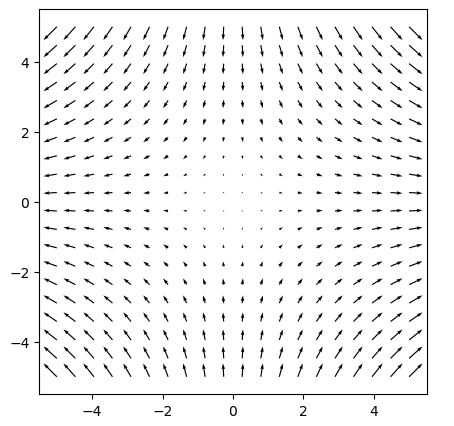
sampleを20まで落としたことに注意。矢印が多すぎると、密集して何が起こっているのかわからなくなってしまいます。

もし各点での矢印の大きさを統一したいならば、「PyPlot.quiver(x, y, u./speed, v./speed)」と大きさで割ると良いでしょう。

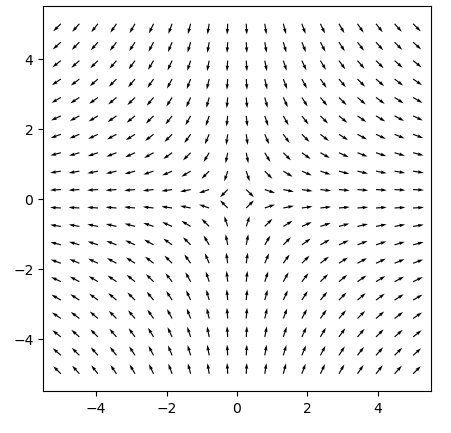
以上、Julia（PyPlot）で2次元のベクトル場・流線を描く方法を紹介してきました。

Plotsで描く方法を探していたのですが、良い出力を得る方法が見つからなかったので、Pyplotを利用することになりました。ベクトル場を手書きするのは大変なので、コンピュータで描けると嬉しいですね。

木村すらいむ（@kimu3_slime）でした。ではでは。

1から始める Juliaプログラミング

posted with AmaQuick at 2021.10.29

進藤 裕之(著), 佐藤 建太(著)
コロナ社 (2020-03-26T00:00:01Z)

￥7,353 (コレクター商品)

Amazon.co.jpで詳細を見る

こちらもおすすめ

ベクトル値関数をベクトル場として描いてみよう：ヤコビ行列と線形近似

流体の複素ポテンシャル、速度ポテンシャル、流れ関数、流線とは