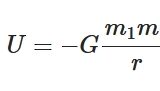クーロン力による位置エネルギーを微積分によって導出

どうも、木村（@kimu3_slime）です。

今回は、クーロン力（静電気力）による位置エネルギー（クーロンポテンシャル）

\[ \begin{aligned}U = qV\\ =k \frac{q_1 q_2}{r}\end{aligned} \]

の微積分による導出を紹介します。

まず、状況設定を確認しましょう。電気量が\(q_1,q_2\)の点電荷があり、その間の距離を\(r\)とします。このとき、点電荷に働く力は

\[ \begin{aligned}F= k\frac{q_1 q_2}{r^2}\end{aligned} \]

と表されます。\(q_1,q_2\)が同符号なら反発力、異符号なら引力です。比例定数\(k=\frac{1}{4\pi \varepsilon_0}\)は、クーロン定数と呼ばれる値です。

クーロン力と万有引力の式はとてもよく似ています。位置エネルギーの形も似ているので、セットで覚えると良いでしょう。

参考：万有引力の位置エネルギーを微積分で導出・証明

では、クーロン力による位置エネルギーを導出していきましょう。\(q_1\)の点電荷の質量を\(m\)とすると、運動方程式\(ma =F\)から、

\[ \begin{aligned}m a = k\frac{q_1 q_2}{r^2}\end{aligned} \]

となります。ここでエネルギー保存の法則と同様に、速度\(v \)をかけましょう。

\[ \begin{aligned}mav = k\frac{q_1 q_2}{r^2}v\end{aligned} \]

です。この式は微分によって整理することができて、

\[ \begin{aligned}\frac{d}{dt} (\frac{1}{2}mv^2) = \frac{d}{dt}(-k \frac{q_1 q_2 }{r}) \end{aligned} \]

となります。加速度、速度、位置の定義から\(\frac{dr}{dt} =v\)、\(\frac{dv}{dt} =a\)であること、\(\frac{d}{dt} (\frac{1}{r}) = -\frac{1}{r^2} \frac{dr}{dt}\)に注意。

左辺に項をまとめて、\(t\)について積分すれば、微積分学の基本定理から

\[ \begin{aligned}\frac{1}{2}mv^2 +k \frac{q_1 q_2 }{r} = C\end{aligned} \]

となります。第一項目を運動エネルギー、第二項目を位置エネルギーと呼びます。

積分範囲をより明確にして計算してみましょう。時刻\(t_1\)から\(t_2\)、距離が\(r_1=r(t_1)\)から\(r_2=r(t_2)\)に変化するときの位置エネルギーは、

\[ \begin{aligned} &\Delta U \\ &= \int_{t_1}^{t_2}\frac{d}{dt}(-k \frac{q_1 q_2 }{r}) dt\\&= [-k \frac{q_1 q_2 }{r(t)}]_{t_1}^{t_2} \\ &= k q_1q_2(\frac{1}{r_1} – \frac{1}{r_2}) \end{aligned} \]

となります。

万有引力によるエネルギーと同じように、一方の基準点を\(r_2 =\infty\)と無限遠点を選ぶことが多いです。このとき、位置エネルギーは広義積分となり、

\[ \begin{aligned} & U \\ &=\lim_{r_2 \to \infty}\Delta U \\&= \lim_{r_2 \to \infty}(k q_1q_2(\frac{1}{r_1} – \frac{1}{r_2})) \\ &= k\frac{q_1q_2}{r_1} \end{aligned} \]

と求めたい形が得られました。

基準点を\(r_2 = \infty\)と選ぶのは、\(U(r) = k\frac{q_1q_2}{r}\)において、\(\lim_{r\to \infty }U(r)=0\)と位置エネルギーが0になり、式がシンプルだからです。

\(q_1,q_2\)が同符号、反発力のときは位置エネルギーは常に正です。\(q_1,q_2\)が異符号、引力のときは位置エネルギーは常に負になります。後者は万有引力による位置エネルギーと全く同じ性質です。

以上、クーロン力による位置エネルギーを微積分によって導出してきました。

力学的エネルギーや万有引力によるエネルギーの導出とセットで覚えると、このテーマは統一的に理解できるでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。