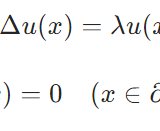偏微分方程式とその力学系、関数解析の入門記事まとめ

どうも、木村（@kimu3_slime）です。

僕が学生時代に専門的に学んだ、偏微分方程式とその力学系、関数解析への入門を紹介します。

微積分学と線形代数学、集合と位相、応用解析の一部（常微分方程式・フーリエ解析・偏微分方程式）が前提知識です。

何のためにこうした基礎分野があるのか、基礎知識は専門的な学びのどこで必要となってくるのか整理しようとする試みです。

概念のモチベーションを紹介することを目標としているため、応用的な話→基礎的な話の順に並んでいる部分があります。興味を持った部分から読み進めてみてください。

力学系、アトラクターの理論
- 常微分方程式の力学系
- 偏微分方程式の力学系
偏微分方程式の基礎、関数空間
- ルベーグ積分、L^p空間
- ソボレフ空間
関数解析
教科書

力学系、アトラクターの理論

力学系理論（dynamical system theory）は、微分方程式の解が長期的にどのような挙動を見せるのかを、初期値の空間（相空間）に注目して調べる分野です。漸近挙動（asymptotic behavior）、長期挙動（long-time behavior）の理論とも。

平衝解は他の解を引き寄せるかどうかは、安定性の理論と呼ばれています。こうした安定性の話は、基本的に平衝解の近くの話：局所的です。

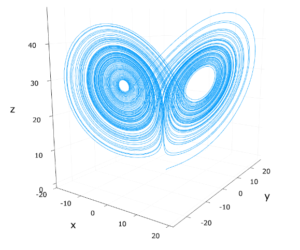
これに対し、アトラクター（attractor）は初期値の空間全体の挙動を捉えようとする大域的な話となります。ローレンツアトラクターは一般に知名度があり、予測不可能性やカオスの話の引き合いに出されますが、まずアトラクターの意味と重要性を知ることは大事です。つまり、微分方程式を理論的に解くのが難しく、個別の解の挙動が予想し難いとしても、およそ限られた範囲に引き込まれとどまっていくことがわかるのがアトラクターの話です。

アトラクターの理論は、まず常微分方程式のケースから学ぶと良いでしょう。しかしそのアイデアは、抽象力学系を通して偏微分方程式でも利用できます。熱方程式を含むような偏微分方程式の分類：反応拡散方程式におけるアトラクターの存在が示せます。

常微分方程式の力学系

カオス理論、バタフライ・エフェクトとは何か？ローレンツ・アトラクターを例に

カオス現象のわかりやすい具体例を視覚的に見る

吸収集合、散逸系とは：線形力学系を例に

一点と集合の距離、集合間の距離とは：ユークリッド空間を例に

グローバルアトラクターとは：散逸系における存在、例

ローレンツ方程式のアトラクターの存在証明

常微分方程式の比較定理とは、証明

グロンウォールの不等式とは、証明

偏微分方程式の力学系

解作用素、抽象力学系とは：偏微分方程式の力学系入門

熱方程式のエネルギー評価とは：単純な例

反応拡散方程式の力学系でL^2の吸収集合が存在することの証明

反応拡散方程式の力学系でアトラクターが存在することの証明

偏微分方程式の基礎、関数空間

偏微分方程式の教科書には、大ざっぱに言えば、関数空間を使わない古典的なアプローチと、関数空間を使った関数解析的なアプローチがあります。ここで紹介するのは後者の入門です。

偏微分方程式の力学系を考えると、相空間はユークリッド空間ではなく、関数のなす空間：関数空間となります。例えば熱方程式の初期状態（初期値）は関数です。

関数空間の典型例が、連続関数のなす空間\(C^k\)、可積分関数のなす空間\(L^p\)、ソボレフ空間\(W^{k,p}\)です。

抽象力学系を定めるためには微分方程式の解の存在と一意性が保証されなければ始まりませんが、一般的な偏微分方程式でそれを示すのは簡単ではありません。

常微分方程式の教科書では、しばしば解の存在と一意性は当たり前で、その上で「解の表示式（公式）を得る」ことを「微分方程式を解く」と呼ぶでしょう。特殊な形の偏微分方程式なら、同様のことができます。

しかし一般的な偏微分方程式では、解の表示式を得るのは難しいです。そこで部分的な問題として、まず解は一意に存在するのかといった基礎的な問題（存在と一意性）を対処しようとするわけです。

\(C^k\)は解の構成、収束について都合が悪いことがあり（完備性がない）、\(L^p\)や\(W^{k,p}\)といったより広い関数空間が必要になります。積分可能な関数だけでは微分の議論ができないため、微分を少し弱めた弱微分、弱形式のアイデアが必要となります。

アトラクターの構成においては、関数空間におけるコンパクト集合が必要となりますが、\(H^1\)の有界集合は\(L^2\)におけるコンパクト集合となる：レシッヒ・コンドラショフの定理のような埋め込み定理は重要です。

ルベーグ積分の教科書や講義はしばしば測度と積分の定義、収束定理に焦点を置きますが、こうした関数空間の準備という目標を持って学ぶのも良いでしょう。

ルベーグ積分、L^p空間

なぜルベーグ積分を学ぶのか偏微分方程式への応用の観点から

連続関数、可積分関数の線形空間（関数空間）、微分と積分の線形性とは

関数空間が無限次元とは？多項式関数を例に

連続関数のなす空間がL^pノルムで完備でないことを示す例

ほとんど至る所（a.e.）とは：簡単な関数を例に

有界閉区間上の連続関数はp乗可積分であることの証明

p乗可積分な関数とは：負のべき乗、L^1だがL^2でない例

ソボレフ空間

テスト関数C_c^∞、関数の台とは：簡単な例

相対位相、部分集合における開集合・閉集合とは：ユークリッド空間の位相を例に

弱微分、ソボレフ空間W^{k,p},H^kとは：簡単な例

弱微分の一意性の証明：変分法の基本補題を利用して

超関数、超関数微分とは：ディラックのデルタ関数を例に

境界で0のソボレフ空間W_0^{k,p},H_0^kとは

弱形式、弱解とは：ポアソン方程式を例に

ソボレフ空間W^{k,p}・H^kが線形、ノルム、内積空間となることの証明

レリッヒ・コンドラショフの定理、コンパクト作用素、コンパクトな埋込みとは

負の指数のソボレフ空間H^{-k}、双対空間とは

ポアンカレの不等式とは、証明、H_0^1ノルムへの応用

時間つき関数空間、バナッハ空間値関数とは

放物型偏微分方程式の弱形式、弱解とは

関数解析

関数解析（functional analysis）は、関数空間と、その要素である関数の対応：作用素や汎関数に関する理論です。主に線形代数がその土台となっています。

常微分方程式の力学系と偏微分方程式の力学系では、相空間はユークリッド空間と関数空間ですが、後者には特有の扱いにくさがあります。まずわかりやすい違いとして、前者は有限次元、後者は無限次元（有限次元でない）があります。

「線形代数」の教科書では、議論を有限次元に制限したものが多いですが、その制限を外した話を関数解析では扱います。

無限次元の場合では「基底」の意味を工夫し、代数的な基底（有限個の線形結合）だけでなく、線形結合の極限として表せる意味での基底：完全正規直交系を考えます。フーリエ級数展開は、関数空間の基底の例です。

有限次元と無限次元では、コンパクトな集合（ある意味で大きすぎない集合）の性質も違います。有限次元では有界な閉集合はコンパクトですが（ハイネ・ボレルの定理）、無限次元ではそうとは限らず、実際単位球がコンパクトになりません。

それでも偏微分方程式の解の存在と一意性を示したり、アトラクターのようなコンパクトな集合を構成するためには、関数空間のノルム（位相）の関係や線形作用素の理論を使いこなす必要があります。

線形作用素は行列の一般化であり、その例である積分作用素や微分作用素は微分方程式と関係してきます。連立方程式\(Ax=b\)を行列として\(x=A^{-1}b\)と解いたように、偏微分方程式を作用素\(F\)によって\(F(u)=v\)と表し、\(v=F^{-1}(u)\)と解けないか考えるわけです。

特にコンパクト作用素は、有限次元の場合の行列の一般化として良い性質を持ちます。対称な行列の固有値は実数で対角化可能という線形代数の結果は、ヒルベルト・シュミットの定理として一般化されます。

関数解析の教科書は、関数空間と線形作用素の一般論が広く展開されますが、一般的すぎて何が目的なのかわからなくなることもあるでしょう。

ここでの一連の記事は、関数解析と偏微分方程式の関連、特にラプラシアンの固有値・固有関数の性質を明らかにします。これは「すべての関数は三角関数の和として表せるか？」というフーリエの問題の正当化と回答、一般化です。また、「ラプラシアンが逆作用素を持つか」という問題は「ポアソン方程式が一意な解を持つか」という問題と等価です。さらに、ラプラシアンの固有値・固有関数は、ポアソン方程式だけでなく、反応拡散方程式などの時間発展する偏微分方程式の解の構成の基礎にもなっています。